2020届二轮复习抛物线及其标准方程课件（20张）（全国通用） 20页

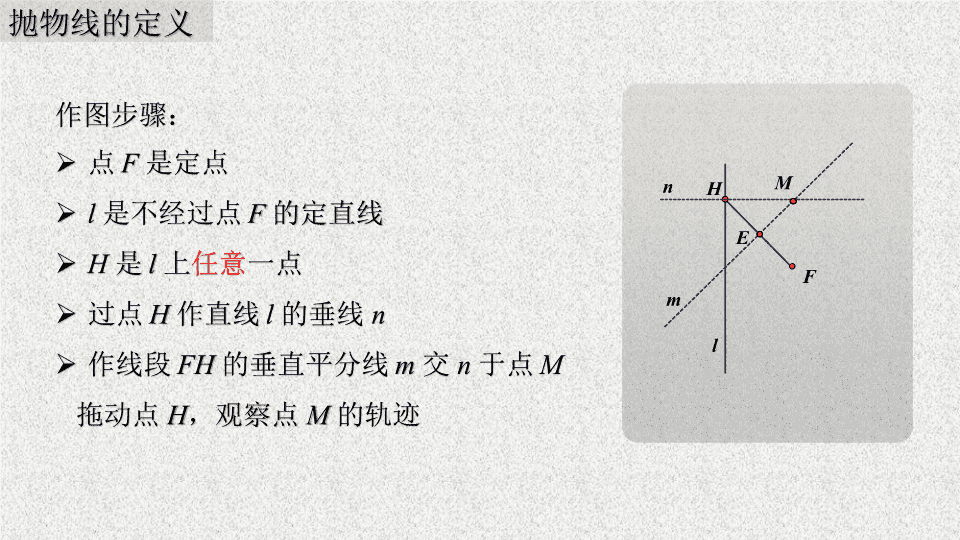
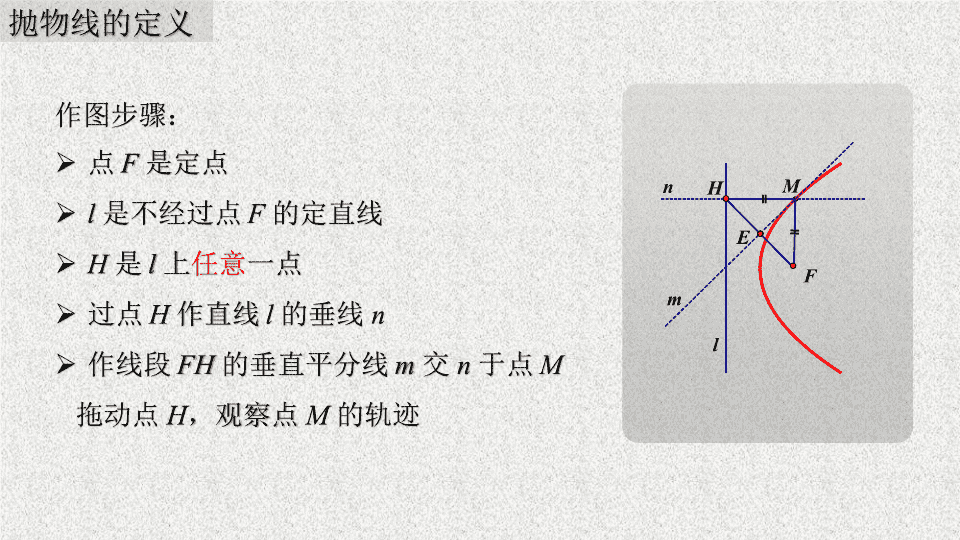
l F 作图步骤： 点 F 是定点 l 是不经过点 F 的定直线 H 是 l 上 任意 一点 过点 H 作直线 l 的垂线 n 作线段 FH 的垂直平分线 m 交 n 于点 M 拖动点 H ，观察点 M 的轨迹 H n m E M 抛物线的定义 M l F H m E n 作图步骤： 点 F 是定点 l 是不经过点 F 的定直线 H 是 l 上 任意 一点 过点 H 作直线 l 的垂线 n 作线段 FH 的垂直平分线 m 交 n 于点 M 拖动点 H ，观察点 M 的轨迹 抛物线的定义 l F H 定义： 我们把平面内与一个定点 F 和一条定直线 l 距离相等的点的轨迹叫做 抛物线 (parabola). 点 F 叫做抛物线的 焦点 ， 直线 l 叫做抛物线的 准线 . M 抛物线的定义 l F H M 定义： 我们把平面内与一个定点 F 和一条定直线 l 距离相等的点的轨迹叫做 抛物线 (parabola). 点 F 叫做抛物线的 焦点 ， 直线 l 叫做抛物线的 准线 . 抛物线的定义 l F H M 定义： 我们把平面内与一个定点 F 和一条 定直线 l ( l 不经过 F ) 距离相等的点的轨 迹叫做 抛物线 (parabola). 点 F 叫做抛物线的 焦点 ， 直线 l 叫做抛物线的 准线 . 抛物线的定义 定义： 我们把平面内与一个定点 F 和一条定直线 l ( l 不经过 F ) 距离相等的点的轨迹叫做抛物线 (parabola). 动动脑，你能根据定义在右图中描出一条抛物线吗？ 抛物线的定义 l F 求抛物线的方程， 如何选择坐标系更简单呢 ? O y x 求抛物线的方程，如何选择坐标系更简单呢 ? l F O y x l F O y x l F O y x P P P H H H K K （方案一） （方案二） （方案三） 设 ( K ) l F O y x P H l F O y x P H K l F O y x P H K 求抛物线的方程，如何选择坐标系更简单呢 ? （方案一） （方案二） （方案三） 设 我们把方程 叫做 抛物线的标准方程 焦点坐标是 准线方程是 l F O y x P H K 练习：若抛物线的标准方程是 你能说出它焦点坐标和准线方程吗？ 抛物线的方程 设 图 形 标准方程 焦点坐标 准线方程 类比 图 形 标准方程 焦点坐标 准线方程 练习 1 ：写出下列抛物线的焦点坐标和准线方程： (1) 练习 焦点： ，准线： 图 形 标准方程 焦点坐标 准线方程 练习 1 ：写出下列抛物线的焦点坐标和准线方程： (1) (2) 练习 焦点： ，准线： 焦点： ，准线： 图 形 标准方程 焦点坐标 准线方程 练习 1 ：写出下列抛物线的焦点坐标和准线方程： (1) (2) (3) 练习 焦点： ，准线： 焦点： ，准线： 焦点： ，准线： 图 形 标准方程 焦点坐标 准线方程 练习 2 ：已知抛物线的焦点是 求它的标准方程 . 练习 3 ：已知抛物线的准线方程是 求它的标准方程 . 练习 4 ：已知抛物线的焦点到准线距离是 求它的标准方程 . 练习 答案： 答案： 答案： , 思考： 二次函数 的图象是抛物线吗？ ？ 抛物面为什么可以聚光呢？ 思考： 抛物面为什么可以聚光呢？ 思考： 抛物面为什么可以聚光呢？ l M m H O y x E F 1 2 3 证明：直线 是抛物线的切线 . 证明：如图 , , 则 , . , 与 联立，化简，可得： , 即：直线 是抛物线的切线 . 思考： 抛物面为什么可以聚光呢？ 应用： 一种卫星接收天线的轴截面如图所示，卫星波束呈近似平行状态射入轴截面为抛物线的接收天线，经反射聚集到焦点处．已知接收天线的口径 ( 直径 ) 为 4.8 m ，深度为 0.5 m ，试建立适当的坐标系，求抛物线的标准方程和焦点坐标．