- 1.96 MB
- 2021-05-22 发布
第
2
讲 数列求和及简单应用
高考导航
演真题
·
明备考
高考体验
1.
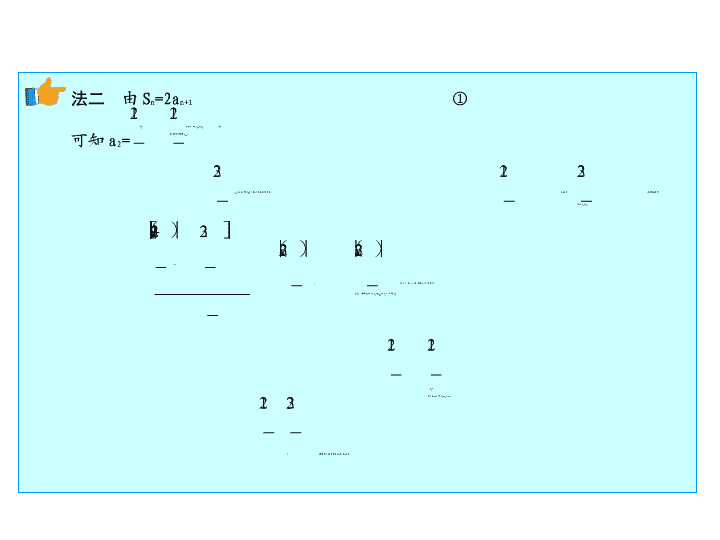
(2012
·
大纲全国卷
,
文
6)
已知数列
{a
n
}
的前
n
项和为
S
n
,a
1
=1,S
n
=2a
n+1
,
则
S
n
等于
(
)
B
2.
(2012
·
新课标全国卷
,
文
12)
数列
{a
n
}
满足
a
n+1
+(-1)
n
a
n
=2n-1,
则
{a
n
}
的前
60
项和为
(
)
(A)3 690 (B)3 660 (C)1 845 (D)1 830
D
3.
(2013
·
全国
Ⅰ
卷
,
文
17)
已知等差数列
{a
n
}
的前
n
项和
S
n
满足
S
3
=0,S
5
=-5.
(1)
求
{a
n
}
的通项公式
;
(2)
求数列 的前
n
项和
.
4.
(2014
·
全国
Ⅰ
卷
,
文
17)
已知
{a
n
}
是递增的等差数列
,a
2
,a
4
是方程
x
2
-5x+6=0
的根
.
(1)
求
{a
n
}
的通项公式
;
(2)
求数列 的前
n
项和
.
高考感悟
1.
考查角度
(1)
以递推公式为背景求通项公式或前
n
项和
,
这类问题还常与函数的性质
(
如周期性质
)
综合命题
.
(2)
以等差数列、等比数列为背景构造新数列
,
利用分组转化、裂项相消、错位相减法求和
.
(3)
根据条件构造等差、等比数列
,
求通项公式或前
n
项和
.
2.
题型及难易度
选择题、填空题、解答题
;
中档题
.
热点突破
剖典例
·
促迁移
求数列的通项公式
热点一
【
例
1】
(1)
(2016
·
湖南衡阳联考
)
已知数列
{a
n
}
满足
a
1
=1,a
n+1
-2a
n
=2
n
(n∈
N
*
),
则数列
{a
n
}
的通项公式为
a
n
=
.
答案
:
(1)n
·
2
n-1
(2)
(2016
·
河北石家庄二模
)
已知数列
{a
n
}
的前
n
项和为
S
n
,
若
S
n
=2a
n
-4,n∈
N
*
,
则
a
n
=
.
解析
:
(2)
因为
S
n
=2a
n
-4, ①
所以
n≥2
时
,S
n-1
=2a
n-1
-4, ②
①-②
得
S
n
-S
n-1
=2a
n
-2a
n-1
,
即
a
n
=2a
n
-2a
n-1
,
所以
a
n
=2a
n-1
,
即
=2.
又
a
1
=S
1
=2a
1
-4,
所以
a
1
=4,
所以数列
{a
n
}
为首项为
4,
公比是
2
的等比数列
,
所以
a
n
=4×2
n-1
=2
n+1
.
答案
:
(2)2
n+1
构造法求通项公式
(1)
本例
(1)
中
,
若将
“
a
n+1
-2a
n
=2
n
”
改为
“
a
n+1
-2a
n
=2
”
,
则
a
n
=
.
(2)
本例
(1)
中
,
若将
“
a
n+1
-2a
n
=2
n
”
改为
“
a
n+1
=
”
,
则
a
n
=
.
【
方法诠释
】
解决此类题目的关键是构造等比数列
,
进而求得
a
n
.
【
方法技巧
】
(1)
利用
S
n
与
a
n
的关系求通项公式
:
通过纽带
:a
n
=S
n
-S
n-1
(n≥2),
消掉
a
n
或
S
n
求解
.
如需消掉
S
n
,
可以利用已知递推式
,
把
n
换成
(n+1)
得到新递推式
,
两式相减即可
.
若要消掉
a
n
,
只需把
a
n
=S
n
-S
n-1
代入递推式即可
.
不论哪种形式
,
需要注意公式
a
n
=S
n
-S
n-1
成立的条件
n≥2.
因此要验证
n=1
是否成立
,
若不成立写成分段形式
.
(2)
由递推关系求通项公式的三种类型及方法
:
①
对形如
a
n+1
=a
n
+f(n)(f(n)
是可以求和的
)
的递推式求通项公式时
,
常用累加法
,
巧妙求出
a
n
-a
1
与
n
的关系式
.
②
对形如
a
n+1
=a
n
f(n)(f(n)
是可以求积的
)
的递推式求通项公式时
,
常用累乘法
,
巧妙求出 与
n
的关系式
.
③
对形如
a
n+1
=ka
n
+b(k≠1,b≠0)(
其中
k,b
为常数
)
的递推式求通项公式时
,
可以构造等比数列
,
先求出该等比数列的通项公式
,
再求
a
n
.
热点训练
:(1)
(2016
·
安徽省
“
江南十校
”
联考
)
已知
S
n
为数列
{a
n
}
的前
n
项和
,
a
1
=1,2S
n
=(n+1)a
n
,
若存在唯一的正整数
n
使得不等式
-ta
n
-2t
2
≤0
成立
,
则实数
t
的取值范围为
.
数列求和
热点二
考向
1
分组求和法
【
例
2】
已知数列
{a
n
}
的前
n
项和为
S
n
,
且满足
a
n
=2-3S
n
(n∈
N
*
).
(1)
求数列
{a
n
}
的通项公式
;
(2)
设
b
n
=log
2
a
n
,
求数列
{a
n
+b
n
}
的前
n
项和
T
n
.
考向
2
裂项相消法
【
例
3】
(2016
·
四川绵阳质检
)
设
S
n
为各项不相等的等差数列
{a
n
}
的前
n
项和
,
已知
a
3
a
5
=3a
7
,S
3
=9.
(1)
求数列
{a
n
}
的通项公式
;
考向
3
错位相减法
【
例
4】
(2014
·
江西卷
,
理
17)
已知首项都是
1
的两个数列
{a
n
},{b
n
}(b
n
≠0,
n∈
N
*
)
满足
a
n
b
n+1
-a
n+1
b
n
+2b
n+1
b
n
=0.
(1)
令
c
n
= ,
求数列
{c
n
}
的通项公式
;
(2)
若
b
n
=3
n-1
,
求数列
{a
n
}
的前
n
项和
S
n
.
解
:
(2)
由
b
n
=3
n-1
知
a
n
=c
n
b
n
=(2n-1)3
n-1
,
于是数列
{a
n
}
前
n
项和
S
n
=1
·
3
0
+3
·
3
1
+5
·
3
2
+
…
+(2n-1)
·
3
n-1
,
3S
n
=1
·
3
1
+3
·
3
2
+
…
+(2n-3)
·
3
n-1
+(2n-1)
·
3
n
,
相减得
-2S
n
=1+2
·
(3
1
+3
2
+
…
+3
n-1
)-(2n-1)
·
3
n
=-2-(2n-2)3
n
,
所以
S
n
=(n-1)3
n
+1.
【
方法技巧
】
(1)
错位相减法适用于由一个等差数列和一个等比数列对应项的乘积构成的数列的求和
.
(3)
分组求和法
:
适用于由等差数列和等比数列的和
(
或差
)
构成的数列
.
数列的综合问题
热点三
(2)
若
c
n
= +2
n
,
求数列
{c
n
}
的前
n
项和
S
n
.
【
方法技巧
】
(1)
解决数列与不等式综合问题的常用方法有比较法
(
作差法、作商法
)
、放缩法等
.
(2)
数列是特殊的函数
,
解题时要充分利用函数的性质解决数列问题
,
如数列中的最值问题
.
备选例题
挖内涵
·
寻思路
解
:
(1)
由
2S
n
=(n+1)
2
a
n
-n
2
a
n+1
,
得到
2S
n-1
=n
2
a
n-1
-(n-1)
2
a
n
,
所以
2a
n
=(n+1)
2
a
n
-n
2
a
n+1
-n
2
a
n-1
+(n-1)
2
a
n
,
所以
2a
n
=a
n+1
+a
n-1
,
所以数列
{a
n
}
为等差数列
,
因为
2S
1
=(1+1)
2
a
1
-a
2
,
所以
4=8-a
2
,
所以
a
2
=4,
所以
d=a
2
-a
1
=4-2=2,
所以
a
n
=2+2(n-1)=2n.
(2)
是否存在正实数
λ,
使得
{b
n
}
为等比数列
?
并说明理由
.
【
例
4】
(2016
·
浙江杭州二模
)
已知数列
{a
n
}
满足
a
1
=3,
当
n>1
时
,
有
a
n
+n=2a
n-1
+2.
(1)
证明
:
数列
{a
n
-n}
是等比数列
,
并求数列
{a
n
}
的通项公式及其前
n
项和
S
n
;
(2)
若数列
{b
n
}
满足
b
n
=(-1)
n
·
a
n
,
试求数列
{b
n
}
的前
n
项和
T
n
.
点击进入 限时训练