【数学】江西省宜春市奉新县第一中学2019-2020学年高二下学期第一次月考（文） 12页

江西省宜春市奉新县第一中学2019-2020学年 高二下学期第一次月考（文） ‎ ‎(考试时间:120分钟 总分:150分)‎ ‎ 第Ⅰ卷（选择题 共50分）‎ 一、 选择题（本大题共10个小题，每小题5分，共50分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ ‎1、已知点的极坐标为那么它的直角坐标为 A. B. C. D. ‎ ‎2、命题“，”的否定是 （ ）‎ ‎ A. 不存在， B. 存在，‎ C. ， D. ，‎ ‎3、双曲线的一条渐近线的方程为 ( ) ‎ A. B. C. D.‎ ‎4、下列命题是真命题的是（ ）‎ A.“若,则”的逆命题 ‎ B.“若，则”的否定 C. “若都是偶数，则是偶数”的否命题 D. “若函数都是R上的奇函数，则是R上的奇函数”的逆否命题 ‎ ‎5、已知椭圆与双曲线－＝1的焦点相同，且椭圆上任意一点到两焦点的距离之和为10，那么椭圆的离心率等于 （ ） ‎ A. B. C. D. 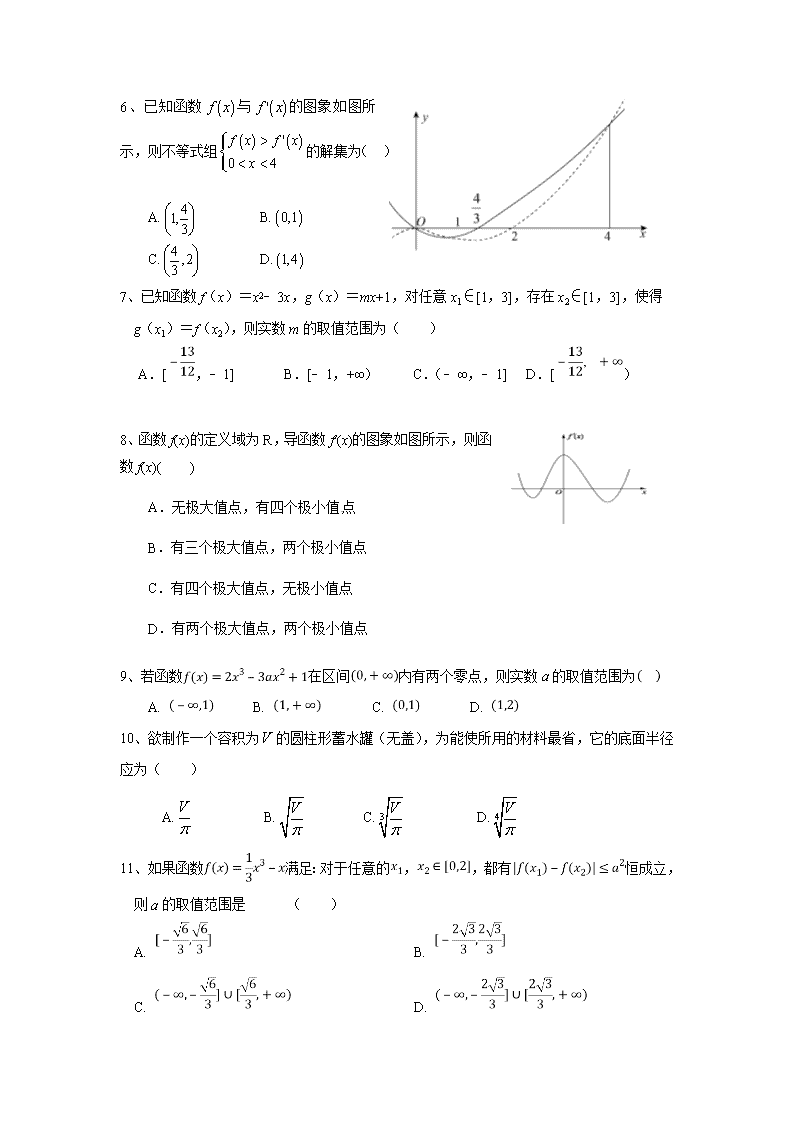‎ ‎6、已知函数与的图象如图所示，则不等式组的解集为（ ）‎ A. B. ‎ C. D.‎ ‎7、已知函数f（x）＝x2﹣3x，g（x）＝mx+1，对任意x1∈[1，3]，存在x2∈[1，3]，使得 g（x1）＝f（x2），则实数m的取值范围为（　　）‎ A．[，﹣1] B．[﹣1，+∞） C．（﹣∞，﹣1] D．[）‎ ‎8、函数f(x)的定义域为R，导函数f′(x)的图象如图所示，则函数f(x)(　　)‎ A．无极大值点，有四个极小值点 ‎ B．有三个极大值点，两个极小值点 C．有四个极大值点，无极小值点 ‎ D．有两个极大值点，两个极小值点 ‎9、若函数在区间内有两个零点，则实数a的取值范围为 A. B. C. D. ‎ ‎10、欲制作一个容积为的圆柱形蓄水罐（无盖），为能使所用的材料最省，它的底面半径应为（ ）‎ A. B. C. D.‎ ‎11、如果函数满足：对于任意的，，都有恒成立，则a的取值范围是 （ ）‎ A. B. ‎ C. D. ‎ ‎12、已知函数是定义在R上的奇函数，为的导函数，且满足当时，有，则不等式的解集为（　　）‎ A．（﹣1，0）∪（1，+∞） B．（﹣∞，0）∪（0，1） ‎ C．（﹣∞，﹣1）∪（1，+∞） D．（﹣1，0）∪（0，1）‎ 第Ⅱ卷（非选择题 共90分）‎ 一、 填空题：（本大题共5小题，每小题5分，共25分.）‎ 13、 已知在上连续可导，为其导函数，且，则在 处的切线方程为________________‎ ‎14、函数的单调减区间是_____ _ ‎ ‎15、抛物线的一条弦被A(4,2)平分，那么这条弦所在的直线方程是 ‎ ‎16、已知函数，若关于x的方程 有3个不同的实数解，则的取值范围是____________‎ 三、解答题：(本大题共6小题，共75分.解答应写出文字说明、证明过程.)[来 ‎17. (本题满分10分) ‎ 已知p：实数x，满足x－a<0，q：实数x，满足x2－4x＋3≤0.‎ ‎（I）若a＝2时，p∧q为真，求实数x的取值范围；‎ ‎（Ⅱ）若p是q的必要不充分条件，求实数a的取值范围 ‎18. (本题满分12分) ‎ 在极坐标系中,极点为,已知曲线为,曲线为,曲线与交于不同的两点.‎ ‎（I）求的值;‎ ‎（Ⅱ）求过点,且与直线平行的直线的极坐标方程.‎ ‎ ‎ ‎19. (本题满分12分) ‎ 已知椭圆的右焦点F(,0)，且点A(2,0)在椭圆上.‎ ‎（I）求椭圆的标准方程;‎ ‎（Ⅱ）过点F且斜率为1的直线与椭圆相交于M、N两点，求.‎ 20. ‎ (本题满分12分) ‎ 已知函数.‎ ‎（Ⅰ）求函数的单调区间；‎ ‎（Ⅱ）判断函数零点的个数，并说明理由.‎ 20. ‎(本题满分12分) ‎ 已知椭圆的离心率为，，分别为椭圆的左、右焦点，‎ 为椭圆上顶点，的面积为． （Ⅰ）求椭圆C的方程； （Ⅱ）若直线与椭圆C交于不同两点M，N，已知，‎ ‎，求实数m的取值范围． ‎ ‎22. (本题满分12分) ‎ 函数． （Ⅰ）讨论函数的单调性； （Ⅱ）当时，方程在区间内有唯一实数解，求实数m的取值范围． ‎ 参考答案 一、选择题（本大题共10个小题，每小题5分，共50分，在每小题所给出的四个选项中，只有一项是符合题目要求的）.‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 A C C D B B A D B C D A 二、填空题：（本大题共5小题，每小题5分，共25分.）‎ ‎13. 14. 15. 16.‎ 三、解答题：(本大题共6小题，共75分.解答应写出文字说明、证明过程.)[来 ‎17. (本题满分10分) ‎ 已知p：实数x，满足x－a<0，q：实数x，满足x2－4x＋3≤0.‎ ‎（I）若a＝2时，p∧q为真，求实数x的取值范围；‎ ‎（Ⅱ）若p是q的必要不充分条件，求实数a的取值范围 ‎(1)由x－a<0，得x3.所以实数a的取值范围是(3，＋∞)．......... 10分 ‎18. (本题满分12分) ‎ 在极坐标系中,极点为,已知曲线为,曲线为,曲线与交于不同的两点.‎ ‎（I）求的值;‎ ‎（Ⅱ）求过点,且与直线平行的直线的极坐标方程.‎ 解(1)∵ρ=2,∴x2+y2=4.又∵ρsin,∴y=x+2.‎ ‎∴|AB|=2=2=2.‎ ‎(2)(方法一)∵直线AB的斜率为1,‎ ‎∴过点(1,0)且与直线AB平行的直线l的直角坐标方程为y=x-1,‎ ‎∴直线l的极坐标为ρsin θ=ρcos θ-1,即ρcos.‎ ‎(方法二)设点P(ρ,θ)为直线l上任一点,因为直线AB与极轴成的角,‎ 则∠PCO=或∠PCO=.‎ 当∠PCO=时,在△POC中,|OP|=ρ,|OC|=1,∠POC=θ,∠PCO=,∠OPC=-θ,‎ 由正弦定理可知,即ρsin,‎ 即直线l的极坐标方程为ρsin.‎ 同理,当∠PCO=时,极坐标方程也为ρsin.‎ 当点P与点C重合时显然满足ρsin.‎ 综上所述,所求直线l的极坐标方程为ρsin.‎ ‎19. (本题满分12分) ‎ 已知椭圆的右焦点F(,0)，且点A(2,0)在椭圆上.‎ ‎（I）求椭圆的标准方程;‎ ‎（Ⅱ）过点F且斜率为1的直线与椭圆相交于M、N两点，求.‎ 解：（1）焦点且过点[来源:学§科§网]‎ 得 又 , ‎ 所以椭圆方程为 . ‎ ‎（2）由题意得，直线的方程为，设 ,‎ 联立直线与椭圆方程，得 ‎ ‎，得， ‎ 则 ‎, ‎ 又,所以 . ‎ 设原点O到直线的距离为d，d==.‎ 所以 .‎ ‎20.(本题满分12分) ‎ 已知函数.‎ ‎（Ⅰ）求函数的单调区间；‎ ‎（Ⅱ）判断函数零点的个数，并说明理由.‎ 解：（Ⅰ）由题意得， ‎ 令，得，． ‎ 与在区间上的情况如下:‎ ‎+‎ ‎0‎ ‎_‎ ‎0‎ ‎+‎ 增 减 增 函数在区间，上单调递增;‎ 函数在在区间上单调递减. ……………………8分 ‎(Ⅱ)根据第一问，由函数单调性可知 当时，有极大值；‎ 当时，有极小值；‎ 在区间单调递增，在区间上单调递减，可知在上，恒有；‎ 当时， ，(举例不唯一)上单调递增，由零点存在定理可知， ‎ 有且只有一个实数，使得.‎ 所以函数有且只有一个零点 ……………12‎ ‎21. (本题满分12分) ‎ 已知椭圆的离心率为，，分别为椭圆的左、右焦点，‎ 为椭圆上顶点，的面积为． （Ⅰ）求椭圆C的方程； （Ⅱ）若直线与椭圆C交于不同两点M，N，已知，‎ ‎，求实数m的取值范围． 解：由题意，， 又，，解得：，，椭圆C的方程为． 由，消去y整理得：， 设，，则， 由， 又设MN中点D的坐标为， ， 即， ，，即，， ‎ ‎，解得的取值范围． 22. (本题满分12分) ‎ 函数． （Ⅰ）讨论函数的单调性； （Ⅱ）当时，方程在区间内有唯一实数解，求实数m的取值范围． 【答案】解：，， 当时，，令 得，令，得， 函数在上单调递增，上单调递减；      当时，令，得，，      令 ，得，，令，得， 函数在和上单调递增，上单调递减；   当时，，函数在上单调递增； 当时，  ， 令 0'/>，得，，令，得， 函数在和上单调递增，上单调递减；    综上所述：当时，函数的单调递增区间为，单调递减区间为； 当时，函数的单调递增区间为和，单调递减区间为； 当时，函数的单调递增区间为； 当时，函数的单调递增区间为和，单调递减区间为， 当时，， 由，得，又，所以， 要使方程在区间上有唯一实数解， 只需有唯一实数解， 令，，‎ ‎， 由 0'/>得，由得， 在区间上是增函数，在区间上是减函数． ，，， 故或． ‎