【物理】2020届二轮复习第1部分专题1第1讲力与物体的平衡学案 17页

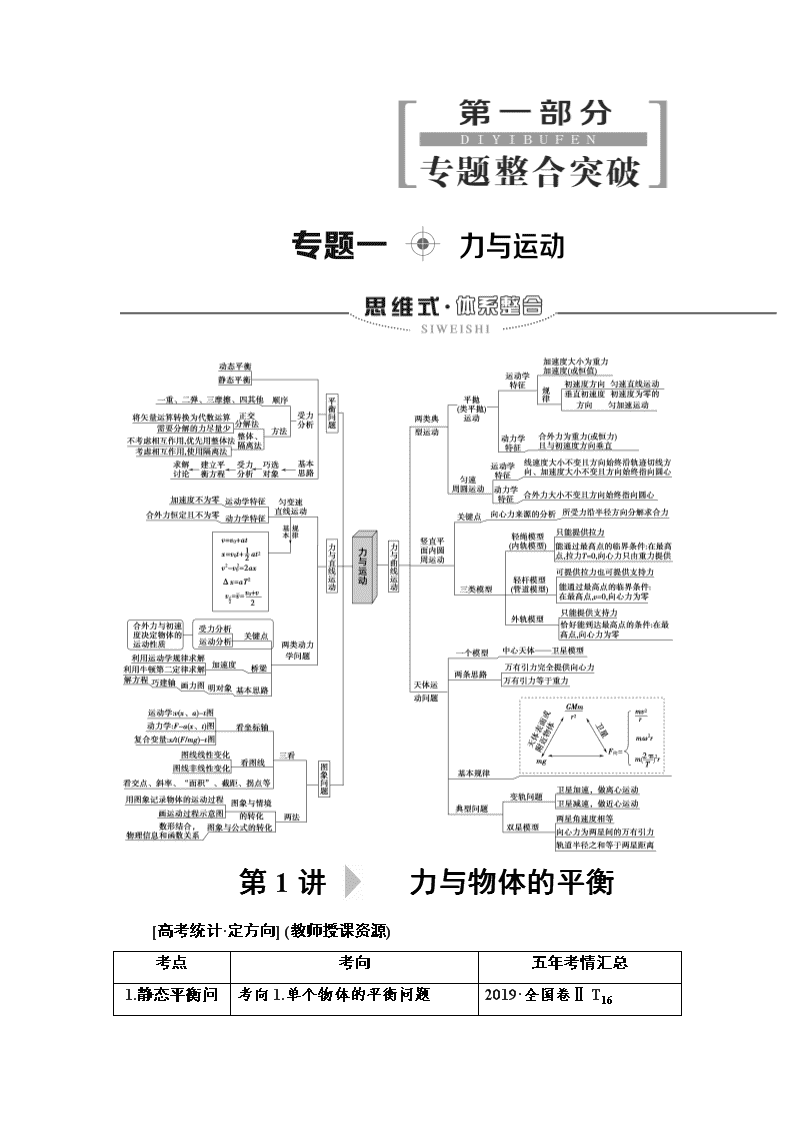
第 1 讲 　 力与物体的平衡 [高考统计·定方向] (教师授课资源) 考点 考向 五年考情汇总 1.静态平衡问 考向 1.单个物体的平衡问题 2019·全国卷Ⅱ T16 2019·全国卷Ⅲ T16 2017·全国卷Ⅲ T17 考向 2.多个物体的平衡问题 2016·全国卷Ⅰ T19 2016·全国卷Ⅲ T17 题 考向 3.电磁场中的平衡问题 2015·全国卷Ⅰ T24 考向 1.解析法 2019·全国卷Ⅰ T19 考向 2.图解法 2016·全国卷Ⅱ T14 2.动态平衡问 题 考向 3.(相似)三角形法 2017·全国卷Ⅰ T21 　静态平衡问题(5 年 6 考) ❶分析近五年的高考题可以看出，高考命题热点集中在物体受力分析、物体 平衡的计算问题，涉及力的合成与分解、整体法和隔离法等常规方法。题型一般 为选择题。 ❷预计在 2020 年高考命题中仍会延续上述特点，复习中要加强多物体静态 平衡和受力分析的训练。 1．(2019·全国卷Ⅱ·T16)物块在轻绳的拉动下沿倾角为 30°的固定斜面向上匀 速运动，轻绳与斜面平行。已知物块与斜面之间的动摩擦因数为 3 3 ，重力加速 度取 10 m/s2。若轻绳能承受的最大张力为 1 500 N，则物块的质量最大为(　　) A．150 kg　　　 B．100 3 kg C．200 kg D．200 3 kg A　[设物块的质量最大为 m，将物块的重力沿斜面方向和垂直斜面方向分解， 由平衡条件可知在沿斜面方向有 F＝mgsin 30°＋μmgcos 30°，解得 m＝150 kg， A 项正确。] 2．(2019·全国卷Ⅲ·T 16)用卡车运输质量为 m 的匀质圆筒状工件，为使工件 保持固定，将其置于两光滑斜面之间，如图所示。两斜面Ⅰ、Ⅱ固定在车上， 倾角分别为 30°和 60°。重力加速度为 g。当卡车沿平直公路匀速行驶时，圆筒 对斜面Ⅰ、Ⅱ压力的大小分别为 F1、F2，则(　　) A．F1＝ 3 3 mg，F2＝ 3 2 mg B．F1＝ 3 2 mg，F2＝ 3 3 mg C．F1＝1 2mg，F2＝ 3 2 m D．F1＝ 3 2 mg，F2＝1 2mg D　[以工件为研究对象，受力分析如图所示，重力与 F′1、F′2 的合力等 大反向，根据共点力平衡条件得F′1 mg ＝cos 30°，F′2 mg ＝cos 60°，则 F′1＝ 3 2 mg，F′2＝1 2mg，根据牛顿第三定律，F1＝F′1＝ 3 2 mg，F2＝F′2＝1 2mg，故 只有 D 选项正确。] 3．(2016·全国卷Ⅲ·T 17)如图所示，两个轻环 a 和 b 套在位于竖直面内的一 段固定圆弧上；一细线穿过两轻环，其两端各系一质量为 m 的小球，在 a 和 b 之间的细线上悬挂一小物块，平衡时，a、b 间的距离恰好等于圆弧的半径，不 计所有摩擦。小物块的质量为(　　) A.m 2 　 　　B. 3 2 m C．m　　 　D．2m [题眼点拨]　①“细线穿过两轻环”“不计所有摩擦”说明细线上张力处处 相等且等于 mg；②“平衡时，a、b 间的距离恰好等于圆弧的半径”说明平衡时， 确定圆弧的圆心，利用对称性分析各力的方向，利用几何关系分析悬挂点的角度 是解题关键。 C　[由于物块通过挂钩悬挂在线上，细线穿过圆环且所有摩擦都不计，可知 线上各处张力都等于小球重力 mg。如图所示，由对称性可知 a、b 位于同一水平 线上，物块处于圆心 O 点正上方，则∠1＝∠2，∠3＝∠4，∠1＝∠5。因圆弧 对轻环的弹力沿圆弧半径方向，且轻环重力不计，由平衡条件知环两侧细线关于 圆弧半径对称，即∠5＝∠6，由几何关系得∠1＝∠2＝∠5＝∠6＝30°，∠3＝∠4 ＝60°。再由物块与挂钩的受力平衡有 mgcos 60°＋mgcos 60°＝Mg，故有 M＝m， C 正确。] [教师备选题] 1．(2017·全国卷Ⅲ·T 17)一根轻质弹性绳的两端分别固定在水平天花板上相 距 80 cm 的两点上，弹性绳的原长也为 80 cm。将一钩码挂在弹性绳的中点，平 衡时弹性绳的总长度为 100 cm；再将弹性绳的两端缓慢移至天花板上的同一点， 则弹性绳的总长度变为(弹性绳的伸长始终处于弹性限度内)(　　) A．86 cm　　B．92 cm　　C．98 cm　　D．104 cm B　[将钩码挂在弹性绳的中点时，由数学知识可知钩码两侧的弹性绳(劲度 系数设为 k)与竖直方向夹角 θ 均满足 sin θ＝4 5 ，对钩码(设其重力为 G)静止时受 力分析，得 G＝2k(1 m 2 －0.8 m 2 )cos θ；弹性绳的两端移至天花板上的同一点时， 对钩码受力分析，得 G＝2k(L 2 －0.8 m 2 )，联立解得 L＝92 cm，故 A、C、D 项错 误，B 项正确。] 2．(多选)(2016·全国卷Ⅰ·T 19)如图所示，一光滑的轻滑轮用细绳 OO′悬挂 于 O 点；另一细绳跨过滑轮，其一端悬挂物块 a，另一端系一位于水平粗糙桌面 上的物块 b。外力 F 向右上方拉 b，整个系统处于静止状态。若 F 方向不变，大 小在一定范围内变化，物块 b 仍始终保持静止，则(　　) A．绳 OO′的张力也在一定范围内变化 B．物块 b 所受到的支持力也在一定范围内变化 C．连接 a 和 b 的绳的张力也在一定范围内变化 D．物块 b 与桌面间的摩擦力也在一定范围内变化 BD　[物块 b 始终保持静止，物块 a 也始终保持静止，绳子对 a 的拉力等于 a 的重力，绳子的夹角 α 也保持不变，OO′绳的拉力也保持不变，选项 A、 C 错误。选 b 为研究对象，在 y 轴方向有 FTcos β＋Fcos γ＋FN＝mbg，由于 FT 不 变，F 变化，所以 FN 也变化，选项 B 正确。FT 和 F 在 x 轴方向的分力和桌面对 b 的摩擦力的合力为零，由于 F 在一定范围内变化，则摩擦力也在一定范围内变 化，选项 D 正确。 ] 3.(2015·全国卷Ⅰ·T 24)如图所示，一长为 10 cm 的金属棒 ab 用两个完全相同 的弹簧水平地悬挂在匀强磁场中；磁场的磁感应强度大小为 0.1 T，方向垂直于 纸面向里；弹簧上端固定，下端与金属棒绝缘。金属棒通过开关与一电动势为 12 V 的电池相连，电路总电阻为 2 Ω。已知开关断开时两弹簧的伸长量为 0.5 cm； 闭合开关，系统重新平衡后，两弹簧的伸长量与开关断开时相比均改变了 0.3 cm。 重力加速度大小取 10 m/s2。判断开关闭合后金属棒所受安培力的方向，并求出 金属棒的质量。 [解析]　依题意，开关闭合后，电流方向从 b 到 a，由左手定则可知，金属 棒所受的安培力方向竖直向下。 开关断开时，两弹簧各自相对于其原长伸长了 Δl1＝0.5 cm。由胡克定律和 力的平衡条件得 2kΔl1＝mg ① 式中，m 为金属棒的质量，k 是弹簧的劲度系数，g 是重力加速度的大小。 开关闭合后，金属棒所受安培力的大小为 F＝IBL ② 式中，I 是回路电流，L 是金属棒的长度。两弹簧各自再伸长了 Δl2＝0.3 cm，由胡克定律和力的平衡条件得 2k(Δl1＋Δl2)＝mg＋F ③ 由欧姆定律有 E＝IR ④ 式中，E 是电池的电动势，R 是电路总电阻。 联立①②③④式，并代入题给数据得 m＝0.01 kg。 ⑤ [答案]　安培力的方向竖直向下，金属棒的质量为 0.01 kg 1．共点力的平衡条件：F 合＝0。 2．多个共点力平衡：任意方向上合力为零，建立直角坐标系后，两个坐标 轴上的合力均为零，即 Fx＝0，Fy＝0。 3．受力分析的三点注意 (1)在分析两个或两个以上物体间的相互作用时，一般采用整体法与隔离法 进行分析(如上 T2 采用隔离法)。 (2)采用整体法进行受力分析时，要注意系统内各个物体的状态应该相同。 (3)当直接分析一个物体的受力不方便时，可转移研究对象，先分析另一个 物体的受力，再根据牛顿第三定律分析该物体的受力，此法叫“转移研究对象 法”。 4．求解共点力平衡问题的常用方法 常用方法包括力的合成法、分解法及正交分解法，以 T2 为例分析如下： 合成法　　　分解法　　　正交分解法 (多选)如图所示，质量分别为 m1、m2 的两个物体通过轻弹簧连接， 在力 F 的作用下一起沿水平方向做匀速直线运动，m1 在地面上，m2 在空中。此 时力 F 与水平方向成 θ 角，弹簧中弹力大小为 F1，弹簧轴线与水平方向的夹角 为 α，m1 受地面的摩擦力大小为 Ff，则下列说法正确的是(　　) A．θ 一定大于 α　 B．θ 可能等于 α C．F 一定大于 F1 D．F 一定大于 Ff [题眼点拨]　①“F 与水平方向成 θ 角”明确力的方向。②“通过轻弹簧连 接”说明弹簧上的拉力处处相等。 ACD　[m2 受三力平衡：m2g、F、F1，根据平衡条件知，F 与 F1 的水平分 力大小相等，即：Fx＝Fcos θ＝F1cos α，F 的竖直分力比 F1 的竖直分力大，即： Fy＝Fsin θ＝F1sin α＋m2g，根据 F 合＝ F2x＋F2y，所以 F>F1，根据 tan θ＝Fy Fx ， 所以 θ>α。根据整体法得：Fcos θ＝Ff，所以 F>Ff，故 A、C、D 正确，B 错误， 故选 A、C、D。] 反思：先用隔离法对m2 受力分析，根据平衡条件列出方程，从而判断 F 与 F1、θ 与 α 的大小关系。再利用整体法对 m1、m2 整体受力分析，根据平衡条 件列出方程，从而判断 F 与 Ff 的大小关系。 考向 1　单个物体的平衡问题 1.(2019·泉州市高中毕业班单科质检)如图所示，总重为 G 的吊灯用三条长度 相同的轻绳悬挂在天花板上，每条轻绳与竖直方向的夹角均为 θ，则每条轻绳对 吊灯的拉力大小为(　　) A. G 3cos θ B. G 3sin θ C.1 3Gcos θ D.1 3Gsin θ A　[对吊灯受力分析，每根绳应在竖直方向上提供重力的三分之一，设轻绳 的拉力大小为 T，吊灯在竖直方向受力平衡，有：3Tcos θ＝G，可得：T＝ G 3cos θ 。] 考向 2　多个物体的平衡问题 2.(2019·武汉示范高中联考)两个质量均为 m 的 A、B 小球用轻杆连接，A 球 与固定在斜面上的光滑竖直挡板接触，B 球放在倾角为 θ 的斜面上，A、B 均静 止，B 球没有滑动趋势，则 A 球对挡板的压力大小为(重力加速度为 g)(　　) A．mgtan θ B. 2mg tan θ C. mg tan θ D．2mgtan θ D　[根据题述，B 球没有滑动趋势，说明 B 球不受摩擦力作用。竖直挡板 光滑，A 球不受摩擦力作用。把 A、B 看成整体进行受力分析，设挡板对 A 球的 支持力为 F，由平衡条件可得 tan θ＝ F 2mg ，解得 F＝2mgtan θ，由牛顿第三定律 可知，A 球对挡板的压力大小为 2mgtan θ，选项 D 正确。] 3．(2019·合肥市高三一模) 如图所示，倾斜直杆的左端固定在水平地面上，与水平面成 θ 角，杆上穿 有质量为 m 的小球 a 和轻质圆环 b，两者通过一条细绳跨过定滑轮相连接。当 a、b 静止时，Oa 段绳与杆的夹角也为 θ，不计一切摩擦，重力加速度为 g。则 下列说法正确的是(　　) A．a 可能受到 2 个力的作用 B．b 可能受到 3 个力的作用 C．绳对 a 的拉力大小为 mgtan θ D．杆对 a 的支持力大小为 mgcos θ C　[对小球 a 受力分析，如图所示，小球 a 一定受 3 个力的作用，由于 b 为 轻质圆环，因此其不受重力的作用，b 静止时，只受两个力的作用，由力的平衡 条件可知 F＝FNb，A、B 错误；对小球 a 由力的平衡条件可知，沿杆方向有 F′cos θ＝mgsin θ，解得绳对 a 的拉力 F′＝mgtan θ，C 正确；垂直杆方向有 mgcos θ ＝F′sin θ＋FNa，解得 FNa＝mgcos θ－mgsin θtan θ，D 错误。] 考向 3　电磁场中的平衡问题 4.如图所示，两个带电小球 A、B 穿在一根水平固定的绝缘细杆上，并通过 一根不可伸长的绝缘细绳跨接在定滑轮两端，整个装置处在水平向右的匀强电 场中，当两个小球静止时，两侧细绳与竖直方向的夹角分别为 α＝30°和 β＝60°， 不计装置中的一切摩擦及两个小球间的静电力。则 A、B 两球的带电荷量 q1 与 q2 大小之比为(　　) A．q1∶q2＝ 3∶1 B．q1∶q2＝ 3∶2 C．q1∶q2＝1∶ 3 D．q1∶q2＝2∶ 3 C　[分别对两小球受力分析，由力的平衡条件可知，两小球在水平方向的合 力均为零，则小球 A 在水平方向上，有 Tsin 30°＝Eq1，小球 B 在水平方向上， 有 T′sin 60°＝Eq2，T′＝T，则联立可解得 q1∶q2＝1∶ 3，C 正确。] 5.(易错题)如图所示，一质量为 m、长度为 L 的导体棒 AC 静止于两平行的 水平导轨上且与两导轨垂直，通过 AC 的电流为 I，匀强磁场的磁感应强度大小 为 B，方向与导轨平面成 θ 角斜向下，下列说法正确的是(　　) A．AC 受到的安培力大小为 BILsin θ B．AC 可能不受摩擦力作用 C．AC 受到的安培力与摩擦力平衡 D．AC 所受的支持力大小为 BILcos θ＋mg，摩擦力大小为 BILsin θ D　[匀强磁场的磁感应强度与导体棒 AC 是垂直的，故 AC 所受的安培力大 小 F 安＝BIL，A 错误。安培力既垂直于导体棒也垂直于磁场，根据左手定则判 断其方向，作出导体棒 AC 的受力示意图(从 A 看向 C 的平面图)如图所示。由于 重力和支持力在竖直方向，而安培力有水平分力，没有摩擦力这三个力无法平衡， 所以导体棒一定会受到水平向左的摩擦力，B 错误。由图可知，安培力的方向不 在水平方向，故无法与摩擦力平衡，C 错误。将安培力在水平方向和竖直方向分 解，根据平衡条件可得支持力大小 FN＝BILcos θ＋mg，摩擦力大小 Ff＝BILsin θ， D 正确。] 易错点评：(1)误认为磁感应强度 B 与导体棒 AC 成 θ 角，从而得出 F 安＝ BILsin θ 的错误结果。 (2)判断安培力方向时，易出现左手、右手应用混淆。 　动态平衡问题(5 年 3 考) ❶近五年高考对动态平衡问题的考查，重在体现数形结合思想，应用图解法 或解析法是求解动态平衡问题的常用方法。 ❷在 2020 年高考中仍会体现数形结合的思想，应用图解法和解析法分析求 解动态平衡问题仍是命题热点。 1.(2016·全国卷Ⅱ·T 14)质量为 m 的物体用轻绳 AB 悬挂于天花板上。用水平 向左的力 F 缓慢拉动绳的中点 O，如图所示。用 T 表示绳 OA 段拉力的大小， 在 O 点向左移动的过程中(　　) A．F 逐渐变大，T 逐渐变大 B．F 逐渐变大，T 逐渐变小 C．F 逐渐变小，T 逐渐变大 D．F 逐渐变小，T 逐渐变小 A　[以 O 点为研究对象，受力如图所示，当用水平向左的力缓慢拉动 O 点 时，则绳 OA 与竖直方向的夹角变大，由共点力的平衡条件知 F 逐渐变大，T 逐 渐变大，选项 A 正确。] 2．(多选)(2019·全国卷Ⅰ·T19)如图所示，一粗糙斜面固定在地面上，斜面顶 端装有一光滑定滑轮。一细绳跨过滑轮，其一端悬挂物块 N，另一端与斜面上的 物块 M 相连，系统处于静止状态。现用水平向左的拉力缓慢拉动 N，直至悬挂 N 的细绳与竖直方向成 45°。已知 M 始终保持静止，则在此过程中(　　) A．水平拉力的大小可能保持不变 B．M 所受细绳的拉力大小一定一直增加 C．M 所受斜面的摩擦力大小一定一直增加 D．M 所受斜面的摩擦力大小可能先减小后增加 BD　[对 N 进行受力分析如图所示，因为 N 的重力与水平拉力 F 的合力和 细绳的拉力 T 是一对平衡力，从图中可以看出水平拉力的大小逐渐增大，细绳 的拉力也一直增大，选项 A 错误，B 正确；M 的质量与 N 的质量的大小关系不 确定，设斜面倾角为 θ，若 mNg≥mMgsin θ，则 M 所受斜面的摩擦力大小会一直 增大，若 mNg π 2)。现将重物向右上方缓慢拉起，并保 持夹角 α 不变。在 OM 由竖直被拉到水平的过程中(　　) A．MN 上的张力逐渐增大 B．MN 上的张力先增大后减小 C．OM 上的张力逐渐增大 D．OM 上的张力先增大后减小 AD　[法一：设重物的质量为 m，绳 OM 中的张力为 TOM，绳 MN 中的张力 为 TMN。开始时，TOM＝mg，TMN＝0。由于缓慢拉起，则重物一直处于平衡状态， 两绳张力的合力与重物的重力 mg 等大、反向。 对重物受力分析如图所示，已知角 α 不变，在绳 MN 缓慢拉起的过程中， 角 β 逐渐增大，则角(α－β)逐渐减小，但角 θ 不变，在三角形中，由正弦定理得： TOM sin(α－β)＝ mg sin θ ，(α－β)由钝角变为锐角，则 TOM 先增大后减小，选项 D 正确； 同理知 TMN sin β ＝ mg sin θ ，在 β 由 0 变为π 2 的过程中，TMN 一直增大，选项 A 正确。 法二：利用矢量圆，如图重力保持不变，是矢量圆的一条弦，FOM 与 FMN 夹 角保持不变， 由图知 FMN 一直增大到最大，FOM 先增大再减小，当 OM 与竖直夹角为 β＝ α－90°时 FOM 最大。] 1．动态平衡问题的特点 通过控制某些物理量，使物体的状态发生缓慢地变化，物体状态在变化过 程中始终处于平衡状态，这种平衡称为动态平衡。如上 T1 中“水平向左的 力”“缓慢拉动 O 点”等特征。 2．解答动态平衡问题的三种方法 (1)“解析法”：如果物体受到多个力的作用，可进行正交分解，利用解析 法，建立平衡方程，根据自变量的变化确定因变量的变化。(如上 T3)。 (2)“图解法”：如果物体受到三个力的作用，其中一个力的大小、方向均 不变，并且还有另一个力的方向不变，此时可用图解法，画出不同状态下力的 矢量图，判断各个力的变化情况。(如上 T1 和 T3) (3)“相似三角形法”：此法是图解法的特例，一般研究对象受绳(杆)或其他 物体的约束，且物体受到三个力的作用，其中的一个力大小、方向均不变，另 外两个力的方向都发生变化，可以用力三角形与几何三角形相似的方法。 考向 1　解析法的应用 1．(2019·江西七校高三联考)如图所示，木板 P 下端通过光滑铰链固定于水 平地面上的 O 点，物体 A、B 叠放在木板上且处于静止状态，此时物体 B 的上 表面水平。现使木板 P 绕 O 点缓慢旋转到虚线所示位置，物体 A、B 仍保持静 止，与原位置相比(　　) A．A 对 B 的作用力减小 B．B 对 A 的支持力增大 C．木板对 B 的支持力增大 D．木板对 B 的摩擦力增大 D　[由题意知 A、B 始终处于动态平衡状态，对 A 受力分析知 A 受重力和 B 对 A 的作用力而平衡，所以 A 对 B 的作用力与 A 的重力大小相等，故 A 错误。 当将木板 P 绕 O 点缓慢旋转到虚线所示位置时，B 的上表面不再水平，设 B 的 上表面与水平面间的夹角为 α，则 B 对 A 的支持力为 GAcos αT2 C．T1＝T3T2，选项 B 正确，C、D 错误。] 3.(改编题)(多选)如图所示，在直角框架 MQN 上，用轻绳 OM、ON 共同悬 挂一个物体。物体的质量为 m，ON 呈水平状态。现让框架沿逆时针方向缓慢旋 转 90°，在旋转过程中，保持结点 O 位置不变。则下列说法正确的是(　　) A．绳 OM 上的力一直在减小 B．绳 ON 上的力一直在增大 C．绳 ON 上的力先增大再减小 D．绳 OM 上的力先减小再增大 AC　[选择结点 O 为研究对象，画出结点 O 的受力图，平衡得到矢量三角 形，如图所示。易知轻绳 OM 上的拉力 FM 一直在减小，框架沿逆时针转过 90° 时拉力 FM＝0，轻绳 ON 上的拉力 FN 先增大再减小，选项 B、D 错误，A、C 正 确。] 考向 3　相似三角形法的应用 4．如图所示，小球 A、B 质量均为 m，初始带电荷量均为＋q，都用长为 L 的绝缘细线挂在绝缘的竖直墙上 O 点，A 球紧靠绝缘的墙壁且其悬线刚好竖直， B 球悬线偏离竖直方向 θ 角而静止，如果保持 B 球的电荷量不变，使 A 球的电 荷量缓慢减小，当两球间距缓慢变为原来的1 3 时，下列判断正确的是(　　) A．小球 A 受到细线的拉力大小不变 B．小球 B 受到细线的拉力变小 C．两球之间的库仑力大小不变 D．小球 A 的电荷量减小为原来的 1 27 D　[小球 B 受力如图所示，两绝缘细线的长度都是 L，由相似三角形得G L ＝ T L ＝F d ，解得 T＝G，F＝Gd L ，设 OB 与竖直方向的夹角为 θ，则 sinθ 2 ＝ d 2 L ＝ F 2G ， 细线对 A 的拉力 T′＝G＋Fsin θ 2 ＝G＋F2 2G ，当两球间距离变为原来的1 3 时，F 逐 渐变为 F′＝F 3 ，所以 T′变小，故 A、B、C 错误；由库仑定律得 F＝kQAQB d2 ， F′＝kQ′AQB (1 3d )2 ，解得 Q′A＝ 1 27QA，故 D 正确。]