【物理】2020届二轮复习十二、力学实验学案（江苏专用） 4页

十二、力学实验 基础回扣 ‎　　1.误差 误差种类 产生原因 大小特点 减小方法 系统误差 实验仪器不精密,实验原理不完善,实验方法粗略 总是偏大 或偏小 更新仪器,完善原理,改进实验方法 偶然误差 由于各种偶然因素(如测量、读数不准确)造成的 可大可小 画图像或取平均值 ‎2.有效数字 ‎(1)有效数字的最后一位是测量者估读出来的,是偶然误差的来源。‎ ‎(2)从数的左边第一个不为零的数字算起,如0.012 5 m为三位有效数字。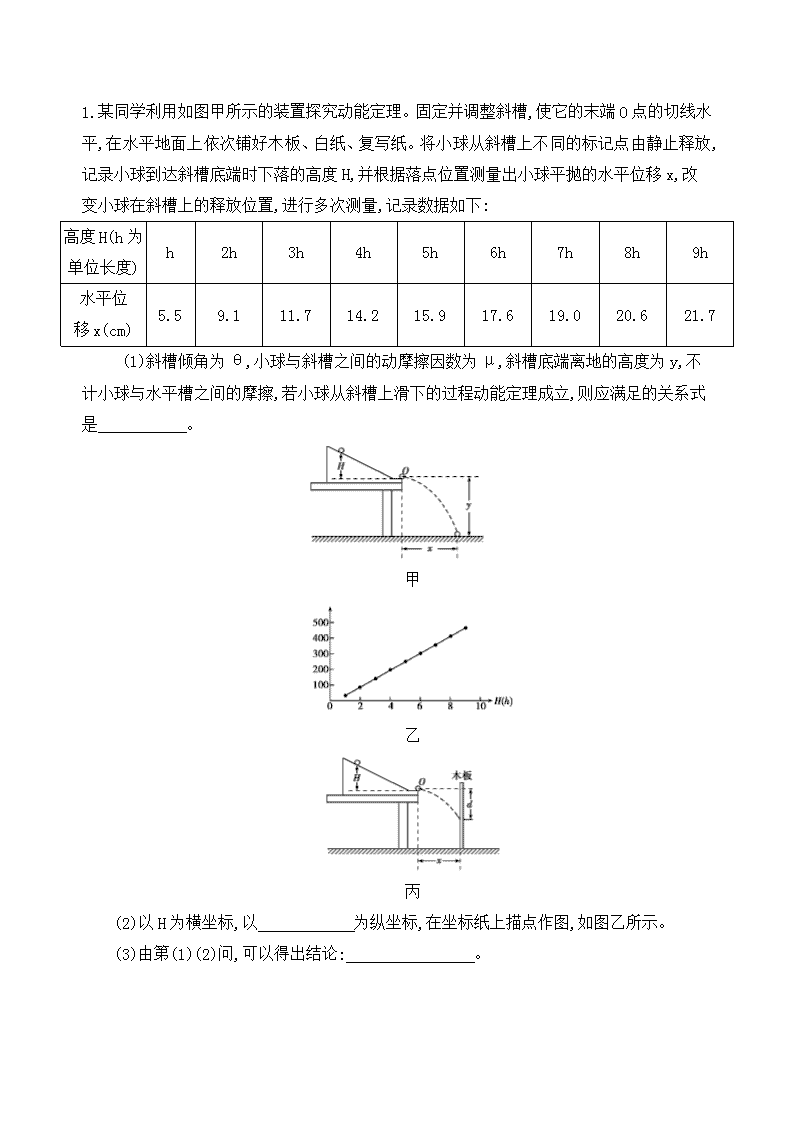‎ ‎3.力学实验要点 分类 实验名称 常考要点 探究性 实验 研究匀变速直线运动 数据处理方法:(1)公式法:vt‎2‎=v、Δx=aT2;(2)图像法:v-t图像 探究弹力与弹簧伸长的关系 注意弹簧的原长,操作注意事项,图像的处理 探究加速度与物体质量、物 体受力的关系 控制变量法的应用、平衡摩擦力、近似法、逐差法、图像的处理以及实验的注意事项 探究动能定理 平衡摩擦力、功采用倍数方式、平均速度、图像法 验证性 实验 验证机械能守恒定律 用自由落体实验,知道如何从纸带中提取数据知道如何确定ΔEp和ΔEk,图像法 验证力的平行四边形定则 弹簧测力计的使用注意事项及读数、力的图示、根据平行四边形定则求出合力 验证动量 守恒定律 测质量、测速度、判断碰撞前后总动量、替代法、平均位置、平均速度等 回归小练 ‎1.某同学利用如图甲所示的装置探究动能定理。固定并调整斜槽,使它的末端O点的切线水平,在水平地面上依次铺好木板、白纸、复写纸。将小球从斜槽上不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并根据落点位置测量出小球平抛的水平位移x,改变小球在斜槽上的释放位置,进行多次测量,记录数据如下:‎ 高度H(h为 单位长度)‎ h ‎2h ‎3h ‎4h ‎5h ‎6h ‎7h ‎8h ‎9h 水平位 移x(cm)‎ ‎5.5‎ ‎9.1‎ ‎11.7‎ ‎14.2‎ ‎15.9‎ ‎17.6‎ ‎19.0‎ ‎20.6‎ ‎21.7‎ ‎ (1)斜槽倾角为θ,小球与斜槽之间的动摩擦因数为μ,斜槽底端离地的高度为y,不计小球与水平槽之间的摩擦,若小球从斜槽上滑下的过程动能定理成立,则应满足的关系式是　　　　　 。 ‎ 甲 乙 丙 ‎(2)以H为横坐标,以　　　　　　为纵坐标,在坐标纸上描点作图,如图乙所示。 ‎ ‎(3)由第(1)(2)问,可以得出结论:　　　　　　　　。 ‎ ‎(4)受该实验方案的启发,另一同学改用图丙的装置实验。他将木板竖直放置在斜槽末端的前方某一固定位置。仍将小球从不同的标记点由静止释放,记录小球到达斜槽底端时下落的高度H,并测量小球击中木板时对应平抛下落的高度d,当他以H为横坐标,以　　　　　　为纵坐标,描点作图,使之仍为一条倾斜的直线,也达到了同样的目的。 ‎ 答案　(1)x2=4(1-μtanθ)yH　(2)x2　(3)见解析　(4)‎‎1‎d 解析　(1)小球在斜槽上运动过程,由动能定理有mgH-μmg cos θ·Hsinθ=‎1‎‎2‎mv2;小球做平抛运动,有x=vt,y=‎1‎‎2‎gt2,解得x2=4(1-μtanθ)yH。‎ ‎(2)要得到题图乙中的线性关系,由x2=4(1-μtanθ)yH可知,以H为横坐标,以x2为纵坐标。‎ ‎(3)由第(1)(2)问,可以得出结论:在实验误差允许范围内,小球运动到斜槽底端的过程中,合力对小球所做的功等于小球动能的增量。‎ ‎(4)另一同学改用题图丙的装置实验,由动能定理有mgH-μmg cos θ·Hsinθ=‎1‎‎2‎mv2;小球做平抛运动有x=vt,d=‎1‎‎2‎gt2,联立解得‎1‎d=‎4‎x‎2‎(1-μtanθ)H。当他以H为横坐标,以‎1‎d为纵坐标,描点作图,使之仍为一条倾斜的直线,也能达到同样的目的。‎ ‎2.如图所示为弹簧弹射装置,在内壁光滑、水平固定的金属管中放有轻弹簧,在其两端各放置一个金属小球1和2(两球直径略小于管径且与弹簧不固定连接),压缩弹簧并锁定。现解除锁定,则两个小球同时沿同一直线向相反方向弹射。按下述步骤进行实验:‎ ‎①用天平测出两球质量分别为m1、m2;‎ ‎②用刻度尺测出两管口离地面的高度均为h;‎ ‎③解除弹簧锁定弹出两球,记录两球在水平地面上的落点P、Q。‎ 回答下列问题:‎ ‎(1)要测定弹射装置在弹射时所具有的弹性势能,还需测量的物理量有　　　　。(已知重力加速度g) ‎ A.弹簧的压缩量Δx B.两球落点P、Q到对应管口M、N的水平距离x1、x2‎ C.小球直径 D.两球从管口弹出到落地的时间t1、t2‎ ‎(2)根据测量结果,可得弹性势能的表达式为Ep=　　　　　　　　　　　　。 ‎ ‎(3)由上述所测得的物理量来表示,如果满足关系式　　　　,那么说明弹射过程中两小球组成的系统动量守恒。 ‎ 答案　(1)B　(2)m‎1‎gx‎1‎‎2‎‎4h+m‎2‎gx‎2‎‎2‎‎4h　(3)m1x1=m2x2‎ 解析　(1)弹簧的弹性势能等于两球得到的动能之和,要求解动能必须还要知道两球弹射的初速度v0,由平抛运动规律,可知v0=x‎2hg,故还需要测出两球落点P、Q到对应管口M、N的水平距离x1、x2,B正确。‎ ‎(2)小球的动能Ek=‎1‎‎2‎mv‎0‎‎2‎=‎1‎‎2‎mxg‎2h‎2‎=mgx‎2‎‎4h;故弹性势能的表达式为Ep=‎1‎‎2‎m1v‎1‎‎2‎+‎1‎‎2‎m2v‎2‎‎2‎=m‎1‎gx‎1‎‎2‎‎4h+m‎2‎gx‎2‎‎2‎‎4h。‎ ‎(3)由测得的物理量来表示,如果满足关系式m1v1=m2v2,即m1x1=m2x2,那么说明弹射过程中两小球组成的系统动量守恒。‎