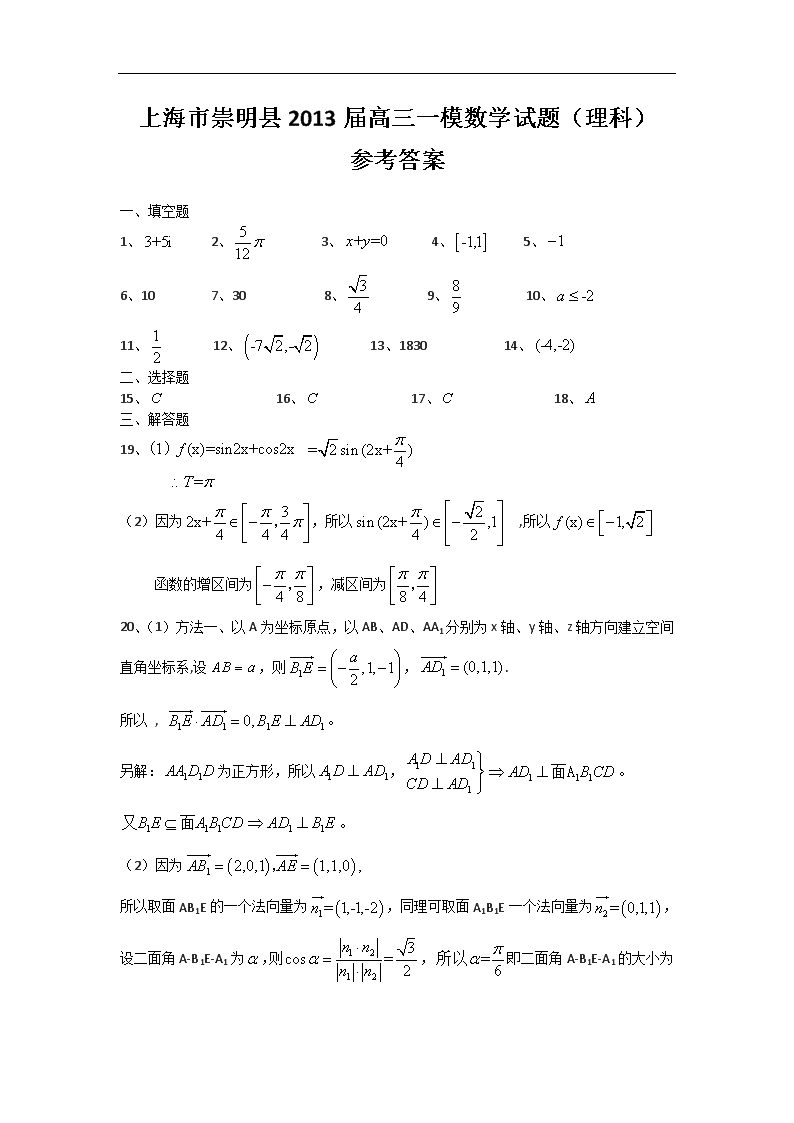2013年上海崇明县高考理科数学一模卷答案 3页

上海市崇明县2013届高三一模数学试题（理科）‎ 参考答案 一、填空题 ‎1、 2、 3、 4、 5、‎ ‎6、10 7、30 8、 9、 10、‎ ‎11、 12、 13、1830 14、‎ 二、选择题 ‎15、 16、 17、 18、‎ 三、解答题 ‎19、 ‎ ‎ ‎ ‎（2）因为，所以 ,所以 ‎ 函数的增区间为，减区间为 ‎ ‎20、（1）方法一、以A为坐标原点，以AB、AD、AA1分别为x轴、y轴、z轴方向建立空间直角坐标系,设，则，. ‎ 所以 , 。‎ 另解：为正方形，所以，。 ‎ ‎。‎ ‎（2）因为 所以取面AB1E的一个法向量为，同理可取面A1B1E一个法向量为， ‎ 设二面角A-B1E-A1为，则，即二面角A-B1E-A1的大小为 ‎. ‎ ‎22、解：（1），令，得，‎ 所以。‎ ‎（2）证明：因为 ，。所以。所以在内存在零点。 ‎ ‎ ，所以在内单调递增，所以在内存在唯一零点。‎ ‎（3）当n＝2时，f2(x)＝x2＋bx＋c.‎ 对任意x1，x2∈[－1,1]都有|f2(x1)－f2(x2)|≤4等价于f2(x)在[－1,1]上的最大值与最小值之差M≤4.‎ 据此分类讨论如下：‎ ‎①当，即|b|＞2时，M＝|f2(1)－f2(－1)|＝2|b|＞4，与题设矛盾。‎ ‎②当－1≤＜0，即0＜b≤2时，M＝f2(1)－f2()＝(＋1)2≤4恒成立． ‎ ‎③当0≤≤1，即－2≤b≤0时，M＝f2(－1)－f2()＝(－1)2≤4恒成立． ‎ 综上可知，－2≤b≤2.‎ 注：②，③也可合并证明如下：‎ 用max{a，b}表示a，b中的较大者．‎ 当－1≤≤1，即－2≤b≤2时，M＝max{f2(1)，f2(－1)}－f2()‎ ‎＝‎ ‎＝1＋c＋|b|－(＋c)‎ ‎＝(1＋)2≤4恒成立．‎ ‎23、解：（1）当三角形面积最大时，为正三角形，所以 ‎ ‎，椭圆E的方程为 ‎ ‎（2）①由，得方程 由直线与椭圆相切得 ‎ 求得，，中点到轴距离 ‎ ‎。‎ 所以圆与轴相交。 ‎ ‎（2）②假设平面内存在定点满足条件，由对称性知点在轴上，设点坐标为， 。‎ 由得 所以，即 所以定点为。 ‎