2019届二轮复习函数的单调性课件（35张）（全国通用） 35页

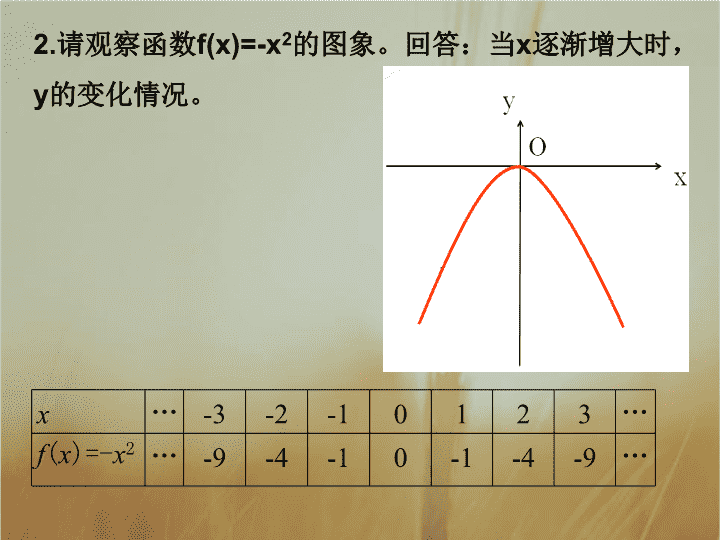
函数的单调性 1. 我们知道篮球从科比手上离开之后划过优美的曲线，落入篮筐。 那请同学们思考一下：篮球投出之后篮球的高度是怎样变化的？ 教学过程： 一、课题导入 : 我们可以得出： 随着篮球的前进篮球高度开始是上升的，达到最高点后是 逐渐 下降的。 2. 请观察函数 f(x)=-x 2 的图象。回答：当 x 逐渐增大时， y 的变化情况。 x … -3 -2 -1 0 1 2 3 … f ( x )=- x 2 … -9 -4 -1 0 -1 -4 -9 … 下面我们以动态的过程来研究函数 f(x)=-x 2 函数值 y 随着 x 的增大的变化情况 O x y x 1 f(x 1 ) O x y x 2 f(x 2 ) O x y x 3 f(x 3 ) O x y x 4 f(x 4 ) O x y x 5 f(x 5 ) O x y x 6 f(x 6 ) O x y x 7 f(x 7 ) O x y x 8 f(x 8 ) O x y x 9 f(x 9 ) 函数 f (x) 在区间上为增函数。 O x y 如何用 x 与 f(x) 来描述上升的图象？ 如何用 x 与 f(x) 来描述下降的图象？ 函数 f (x) 在区间上为减函数。 O x y 在给定区间上任取 x 1 ， x 2 f(x 1 ) ＜ f(x 2 ) x 1 ＜ x 2 f(x 1 ) ＞ f(x 2 ) x 1 ＜ x 2 在给定区间上任取 x 1 ， x 2 如果对于定义域 I 内某个区间 D 上的 任意 两个自变量的值 x 1 、 x 2 ， 当 x 1 ＜ x 2 时， 都有 f(x 1 ) ＜ f(x 2 ) ，那么就说函数 f(x) 在区间 D 上是 增函数 。 定义： 一般的，设函数 f(x) 的定义域为 I ： 如果对于定义域 I 内某个区间 D 上的 任意 两个自变量的值 x 1 、 x 2 ， 当 x 1 ＜ x 2 时， 都有 f(x 1 ) ＞ f(x 2 ) ，那么就说函数 f(x) 在区间 D 上是 减函数 。 O x y O x y 二、讲授新课： 提问：你认为定义中的关键词语是什么？ 如果函数 在 某个区间 是增函数或是减函 数，那么就是说函数 在这个区间 具有 严格的 单调性 ， 这一区间 叫做函数的 单调区间 。 答：定义域，区间，任意，都有。 例 1 如图，是定义在区间 [-4 ， 3] 上的函数 y= f(x ）的图象，根据图象说出 y= f(x ）的单调区间，以及在每个单调区间上， y= f(x ）是增函数还是减函数。 解：函数 的单调区间有 [-4 ， -2 ）， [-2 ， 1 ）， [1 ， 2 ）， [2 ， 3 ） 其中 在区间 [-4 ， -2 ）， [1 ， 2 ） 上是减函数， 在区间 [-2 ， 1 ）， [2 ， 3] 上 是增 函数 三、例题分析： 证明： （条件） （论证结果） （结论） 例2． 证明函数 在 R 上是增函数． 证明函数单调性的步骤： 第一步： 取值 . 即任取区间内的两个值，且 x 1 0 k <0 k >0 k <0 增函数 减函数 减函数 增函数 单调性 函数 单调区间 单调性 增函数 增函数 减函数 减函数 课堂小结 2 、函数单调性的定义； 3 、证明函数单调性的步骤； 1 、单调函数的图象特征； 4 、函数的最值： 最大值 最小值 5 、函数的最值的求法 （ 1 ）利用二次函数的性质（配方法）求函数的最值 ; （ 2 ）利用图象求函数的最值 ; （ 3 ）利用函数单调性求函数的最值 .