2016年高考数学（文科）真题分类汇编G单元 立体几何 25页

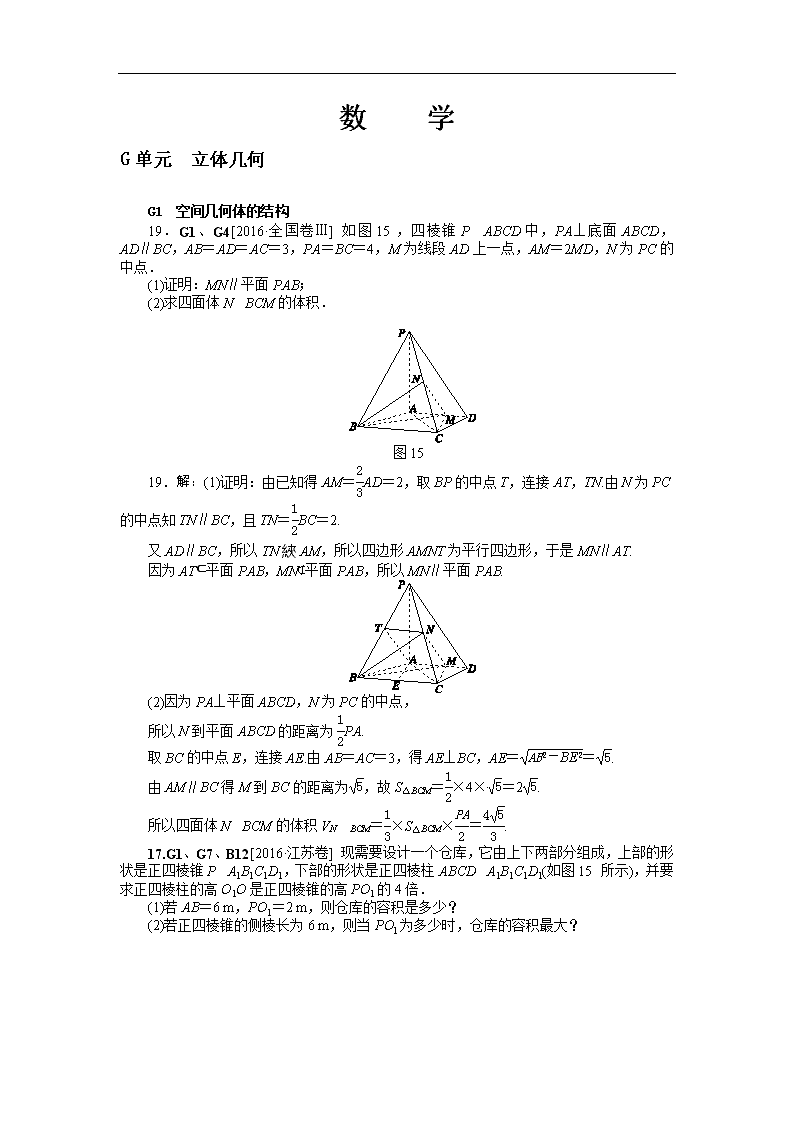
数 学 G单元 立体几何 ‎ G1 空间几何体的结构 ‎ ‎19．G1、G4[2016·全国卷Ⅲ] 如图15，四棱锥P ABCD中，PA⊥底面ABCD，AD∥BC，AB＝AD＝AC＝3，PA＝BC＝4，M为线段AD上一点，AM＝2MD，N为PC的中点．‎ ‎(1)证明：MN∥平面PAB；‎ ‎(2)求四面体N BCM的体积．‎ 图15‎ ‎19．解：(1)证明：由已知得AM＝AD＝2，取BP的中点T，连接AT，TN.由N为PC的中点知TN∥BC，且TN＝BC＝2.‎ 又AD∥BC，所以TN綊AM，所以四边形AMNT为平行四边形，于是MN∥AT.‎ 因为AT⊂平面PAB，MN⊄平面PAB，所以MN∥平面PAB.‎ ‎(2)因为PA⊥平面ABCD，N为PC的中点，‎ 所以N到平面ABCD的距离为PA.‎ 取BC的中点E，连接AE.由AB＝AC＝3，得AE⊥BC，AE＝＝.‎ 由AM∥BC得M到BC的距离为，故S△BCM＝×4×＝2.‎ 所以四面体N BCM的体积VN BCM＝×S△BCM×＝.‎ ‎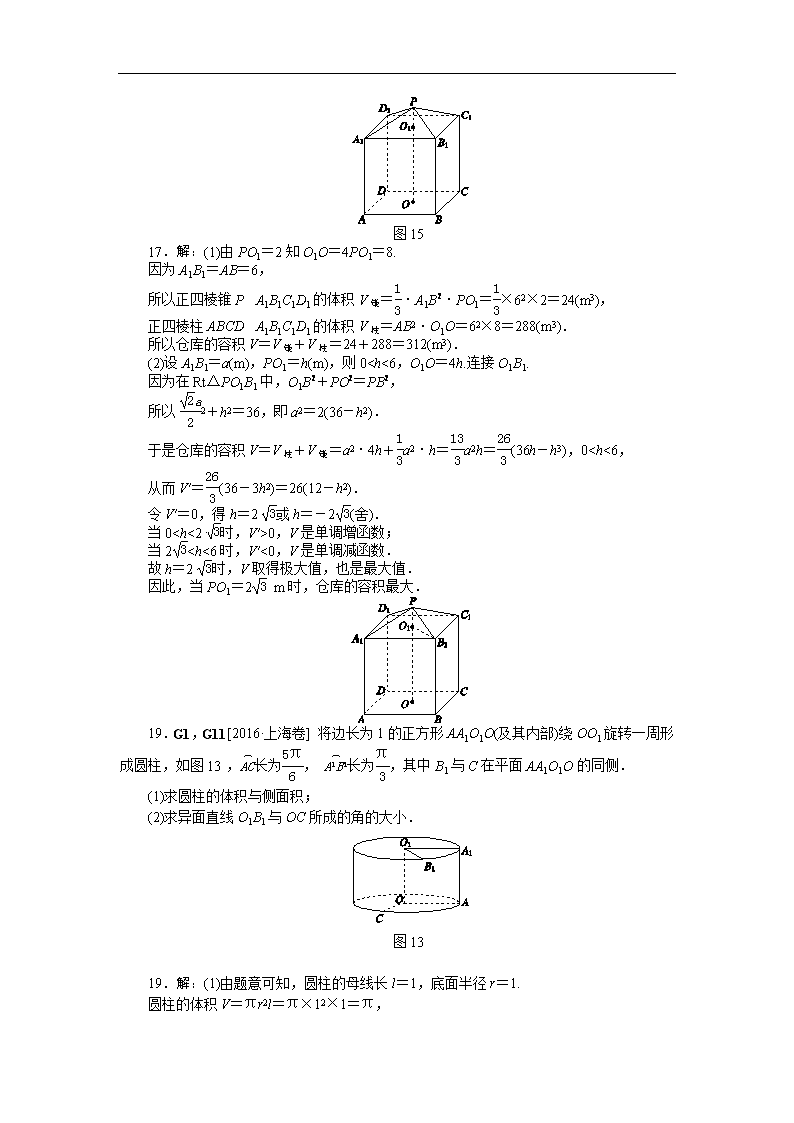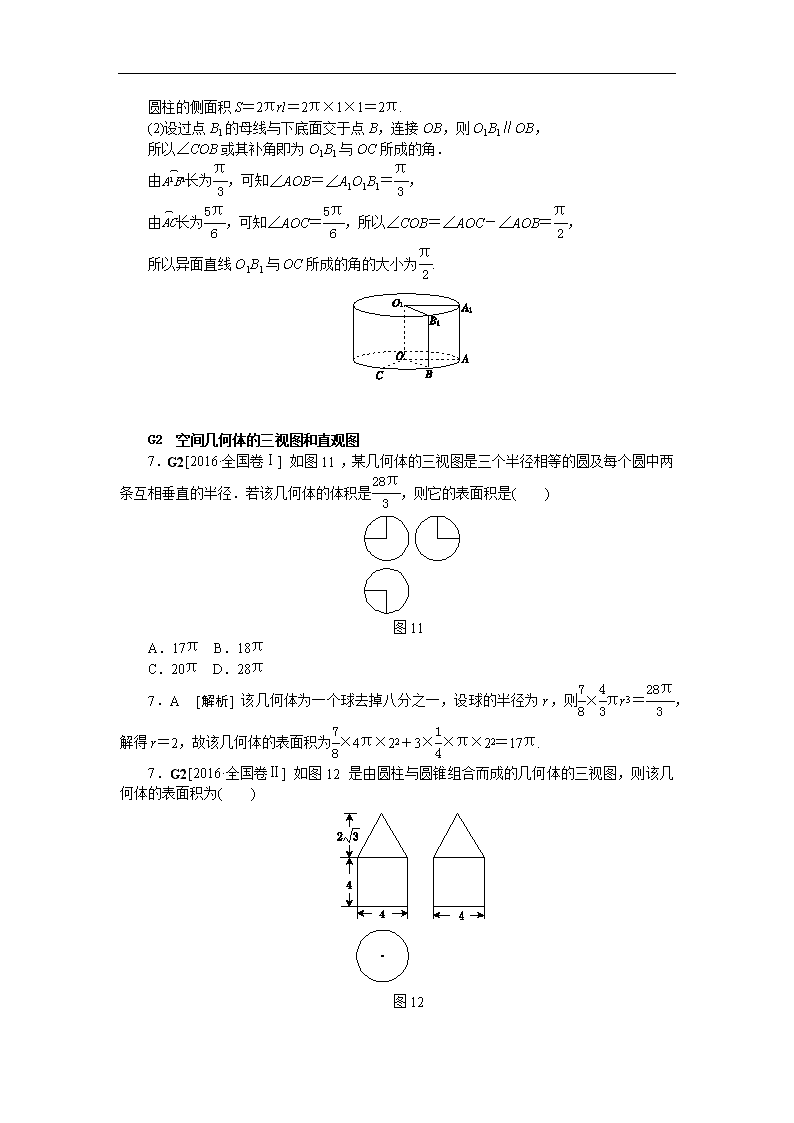17.G1、G7、B12[2016·江苏卷] 现需要设计一个仓库，它由上下两部分组成，上部的形状是正四棱锥P A1B1C1D1，下部的形状是正四棱柱ABCD A1B1C1D1(如图15所示)，并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍．‎ ‎(1)若AB＝6 m，PO1＝2 m，则仓库的容积是多少？‎ ‎(2)若正四棱锥的侧棱长为6 m，则当PO1为多少时，仓库的容积最大？‎ 图15‎ ‎17．解：(1)由PO1＝2知O1O＝4PO1＝8.‎ 因为A1B1＝AB＝6，‎ 所以正四棱锥P A1B1C1D1的体积V锥＝·A1B·PO1＝×62×2＝24(m3)，‎ 正四棱柱ABCD A1B1C1D1的体积V柱＝AB2·O1O＝62×8＝288(m3)．‎ 所以仓库的容积V＝V锥＋V柱＝24＋288＝312(m3)．‎ ‎(2)设A1B1＝a(m)，PO1＝h(m)，则00，V是单调增函数；‎ 当20，V是单调增函数；‎ 当2