高考数学汇编文直线与圆含答案与详解 13页

‎201高考数学汇编（文）---直线与圆 ‎1. 【2014高考安徽卷文第6题】过点的直线与圆有公共点，则直线的倾斜角的取值范围是（ ）‎ A. B. C. D.‎ ‎2. 【2014高考北京卷文第7题】已知圆和两点，，‎ 若圆上存在点，使得，则的最大值为（ ）‎ ‎ A. B. C. D.‎ ‎3. 【2014高考大纲卷文第16题】直线l1和l2是圆的两条切线，若l1与l2的交点为（1,3），则l1与l2的交角的正切值等于 .‎ ‎4.【2014高考福建卷文第6题】已知直线过圆的圆心，且与直线垂直，则的方程是 （ ）‎ ‎5. 【2014高考湖北卷文第17题】 已知圆和点，若定点和常数满足：对圆上那个任意一点，都有，则 ‎（1） ；‎ ‎（2） .‎ ‎6.【2014高考湖南卷文第6题】若圆与圆，则（ ）‎ ‎ ‎ ‎7.【2014高考江苏卷第9题】在平面直角坐标系中，直线被圆截得的弦长为 .‎ ‎8. 【2014高考全国2卷文第12题】设点，若在圆上存在点，使得，则的取值范围是（ ）‎ ‎ （A） （B） （C） （D）‎ ‎9.【2014高考四川卷文第9题】圆心在直线上的圆C与y轴的正半轴相切，圆C截x轴所得的弦的长为，则圆C的标准方程为_______________‎ ‎10.【2014高考四川卷文第9题】设，过定点的动直线和过定点的动直线交于点，则的取值范围是（ ）‎ A、 B、 C、 D、‎ ‎11.【2014高考浙江卷文第5题】已知圆截直线所得弦的长度为4，则实数的值为（ ）‎ A. B. C. 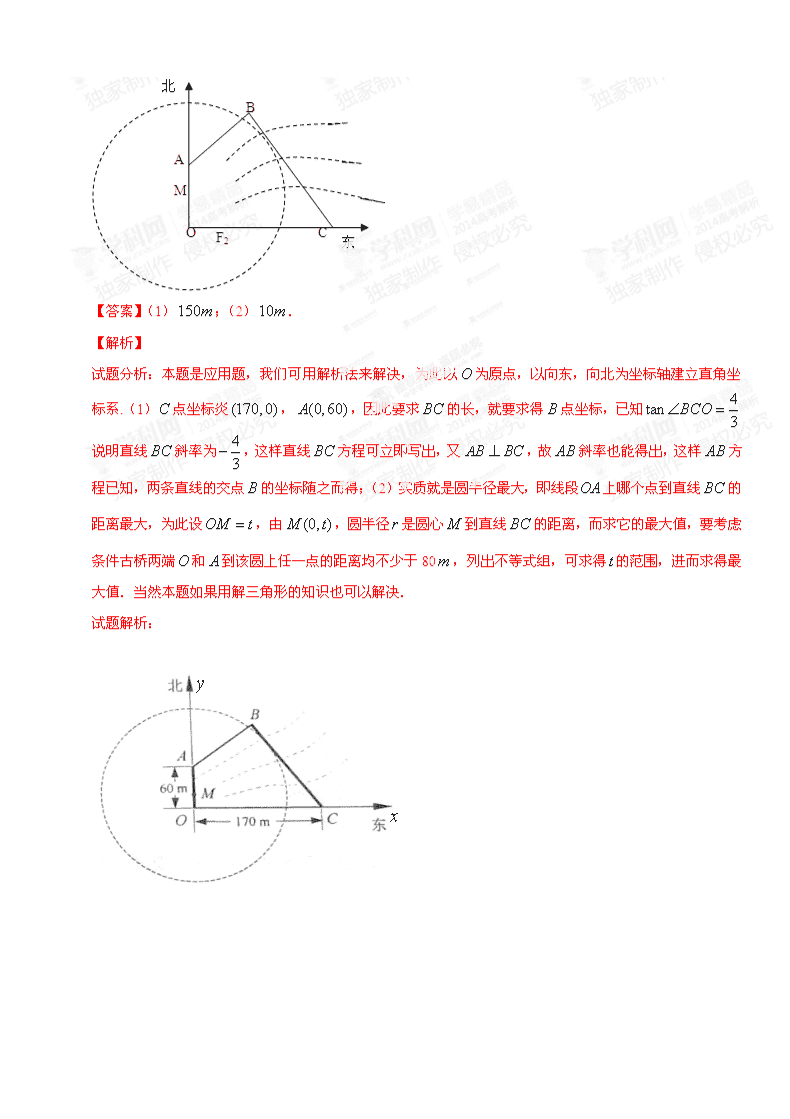D.‎ ‎12.【2014高考重庆卷文第14题】已知直线与圆心为的圆相交于两点，且 ，则实数的值为_________.‎ ‎13. 【2014高考江苏第18题】如图：为保护河上古桥，规划建一座新桥，同时设立一个圆形保护区，规划要求，新桥与河岸垂直；保护区的边界为圆心在线段上并与相切的圆，且古桥两端和到该圆上任一点的距离均不少于80，经测量，点位于点正北方向60处，点位于点正东方向170处，（为河岸），.‎ ‎（1）求新桥的长；‎ ‎（2）当多长时，圆形保护区的面积最大？‎ ‎14.【2014高考全国1文第20题】已知点，圆:，过点的动直线与圆交于两点，线段的中点为，为坐标原点.‎ （1） 求的轨迹方程；‎ （2） 当时，求的方程及的面积 答案与解析：‎ ‎1. 【2014高考安徽卷文第6题】过点的直线与圆有公共点，则直线的倾斜角的取值范围是（ ）‎ A. B. C. D.‎ ‎2. 【2014高考北京卷文第7题】已知圆和两点，，‎ 若圆上存在点，使得，则的最大值为（ ）‎ ‎ A. B. C. D.‎ ‎【答案】B ‎【解析】由题意知，点P在以原点（0，0）为圆心，以m为半径的圆上，又因为点P在已知圆上，所以只要两圆有交点即可，所以，故选B.‎ ‎【考点】本小题主要考查两圆的位置关系，考查数形结合思想，考查分析问题与解决问题的能力.‎ ‎3. 【2014高考大纲卷文第16题】直线l1和l2是圆的两条切线，若l1与l2的交点为（1,3），则l1与l2的交角的正切值等于 .‎ ‎4.【2014高考福建卷文第6题】已知直线过圆的圆心，且与直线垂直，则的方程是 （ ）‎ ‎5. 【2014高考湖北卷文第17题】 已知圆和点，若定点和常数满足：对圆上那个任意一点，都有，则 ‎（1） ；‎ ‎（2） .‎ ‎【答案】（1）；（2）‎ ‎【解析】‎ 试题分析：设，因为，‎ 所以，‎ ‎6.【2014高考湖南卷文第6题】若圆与圆，则（ ）‎ ‎ ‎ ‎7.【2014高考江苏卷第9题】在平面直角坐标系中，直线被圆截得的弦长为 .‎ ‎8. 【2014高考全国2卷文第12题】设点，若在圆上存在点，使得 ‎，则的取值范围是（ ）‎ ‎ （A） （B） （C） （D）‎ ‎10.【2014高考四川卷文第9题】设，过定点的动直线和过定点的动直线交于点，则的取值范围是（ ）学科网 A、 B、 C、 D、‎ ‎11.【2014高考浙江卷文第5题】已知圆截直线所得弦的长度为4，则实数的值为（ ）‎ A. B. C. D.‎ ‎【答案】B ‎ ‎12.【2014高考重庆卷文第14题】已知直线与圆心为的圆相交于两点，且 ，则实数的值为_________.‎ ‎【答案】0或6‎ ‎【解析】‎ 试题分析：圆的标准方程为：,所以圆的圆心在，半径 又直线与圆交于两点，且,所以圆心到直线的距离.所以，，整理得：解得：或.‎ 考点：1、圆的标准方程；2、直线与圆的位置关系；3、点到直线的距离公式.‎ ‎13. 【2014高考江苏第18题】如图：为保护河上古桥，规划建一座新桥，同时设立一个圆形保护区，规划要求，新桥与河岸垂直；保护区的边界为圆心在线段上并与相切的圆，且古桥两端和到该圆上任一点的距离均不少于80，经测量，点位于点正北方向60处，点位于点正东方向170处，（为河岸），.‎ ‎（1）求新桥的长；‎ ‎（2）当多长时，圆形保护区的面积最大？‎ ‎14.【2014高考全国1文第20题】已知点，圆:，过点的动直线与圆交于两点，线段的中点为，为坐标原点.‎ （1） 求的轨迹方程；‎ （2） 当时，求的方程及的面积