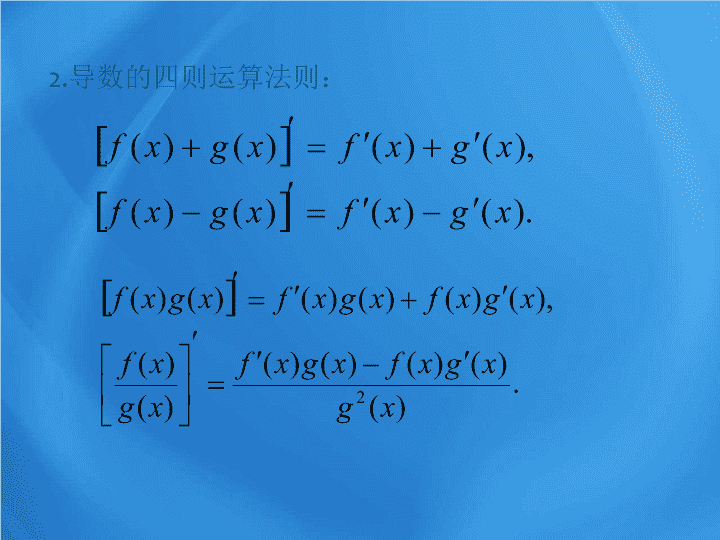- 491.26 KB
- 2021-05-08 发布
第二章 变化率与导数
§5
简单复合函数的求导法则
知识回顾
函数
导函数
1
、导数公式表
2.
导数的四则运算法则:
课前练习:
1.
复合函数的概念
:
讲授新课:
1.
指出下列函数是怎样复合而成:
本节巩固练习
其实, 是一个复合函数,
问题:
分析三个函数解析式以及导数
之间的关系
:
①
②
2.
复合函数的导数
:
注意:
1
、
法则可以推广到两个以上的中间变量
;
2
、求复合函数的导数
,
关键在于分清函数的复合关系
,
合理选定中间变量
,
明确求导过程中每次是哪个变量相对于哪个变量求导
.
复合函数的求导法则
:
复合函数对自变量的导数
,
等于已知函数对
中间变量
f(u)
的导数
,
乘以中间变量 对自变量的导数
.
讲授新课:
【
解析
】
解:
(2)y′=(sin
3
x+sinx
3
)′
=(sin
3
x)′+(sinx
3
)′
=3sin
2
x
·
(sinx)′+cosx
3
·
(x
3
)′
=3sin
2
xcosx+3x
2
cosx
3
.
【
解析
】
自学课本:本节例
3
例
3.
求下列复合函数的导数
解
:(1)
所以由复合函数求导法则得
(
3
)
计算熟练后,在计算复合函数求导时可不必写出中间变量,直接计算
(
2
)
例
4
.
求下列函数的导数
解
:(
1)
(
2
)
本节巩固练习
2.
填空题
3.
求下列复合函数的导数
21:42:35