2018-2019学年山西省运城中学、芮城中学高二上学期期中联考数学（理）试题 Word版 9页

运城中学、芮城中学 ‎2018-2019学年第一学期期中考试 高二数学试题（理）‎ ‎（本试题共150分，时间120分钟。答案一律写在答题卡上）‎ 一、选择题(本大题共12小题,每小题5分,满分60分,在每小题给出的四个选项中,只有一项是符合题目要求的.)‎ ‎1.空间直角坐标系中，点关于点的对称点的坐标是 A.(－10,2,8) B.(－10,2,－8) C.(5,2,－8) D.(－10,3,－8) ‎ ‎2.直线的倾斜角为 ‎ A. B. C. D.‎ ‎3.已知m，n是两条不同的直线，α，β，γ是三个不同的平面，则下列命题正确的是 A.若α⊥γ，α⊥β，则γ∥β B.若m∥n，m⊂α，n⊂β，则α∥β C.若m∥n，m∥α，则n∥α D.若n⊥α，n⊥β，则α∥β ‎4.直线：与圆交于两点，，则实数的值为 A. B. C. D.‎ ‎5.在直三棱柱中，，，则其外接球的体积为 A.　　　　 B. C.　　　　 D.‎ ‎6.如图是一个几何体的三视图，根据图中的数据，计算该几何体的表面积为 A.15π　　　　 ‎ B.18π ‎ C.22π　　　　 ‎ D.33π ‎7.三棱锥中，，，，则二面角等于 A. B. ‎ C.　　 D.‎ ‎8.在体积为15的斜三棱柱ABC－A1B1C1中，S是C1C上的一点，三棱锥S－ABC的体积为3，则三棱锥S－A1ABB1的体积为 ‎ A.11 B.‎ C.10 D.9‎ ‎9.若曲线C1：x2＋y2－2x＝0与曲线C2：y(y－mx+3m)＝0有四个不同的交点，则实数m的取值范围是 A. B.‎ C. D.‎ ‎10.已知圆，圆，分别为圆和圆上的动点，为直线上的动点，则的最小值为 ‎ A. B. C. D.‎ ‎11.若圆上总存在点A，使得，则实数的取值范围是 ‎ A. B. C. D.‎ ‎12.如图，在边长为2的正方形中，分别为的中点，为的中点，沿将正方形折起，使重合于点，在构成的四面体中，下列结论错误的是 ‎ A.平面 ‎ ‎ B.直线与平面所成角的正切值为 ‎ C.四面体的内切球表面积为 ‎ ‎ D.异面直线和所成角的余弦值为 二、填空题(本大题共4小题,每小题5分，共20分)‎ ‎13.已知直线l1：2x＋my＋1＝0与l2：3x－y－1=0平行，则m的值为_______.‎ ‎14.如图所示，为水平放置的的直观图，其中，，则的面积是 。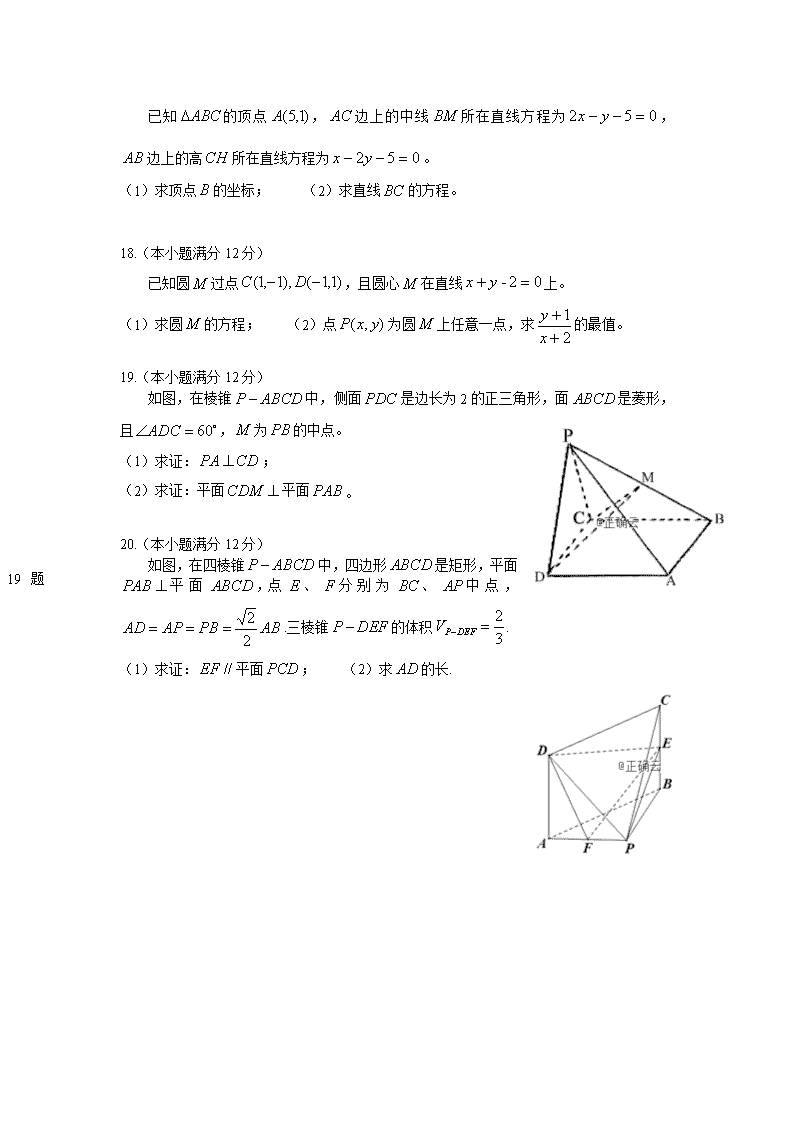‎ ‎15.某三棱锥的三视图如图所示，则其所有面中，面积最大的面的面积为 .‎ ‎16.过动点作圆的切线，其中为切点，若（为坐标原点），则的最小值为______.‎ 三、解答题(本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.)‎ ‎17.（本小题满分10分）‎ 已知的顶点，边上的中线所在直线方程为，边上的高所在直线方程为。‎ （1） 求顶点的坐标； （2）求直线的方程。‎ ‎18.（本小题满分12分）‎ 已知圆过点，且圆心在直线上。‎ ‎（1）求圆的方程； （2）点为圆上任意一点，求的最值。‎ ‎19.（本小题满分12分）‎ 如图，在棱锥中，侧面是边长为2的正三角形，面是菱形，且，为的中点。‎ （1） 求证：； ‎ ‎（2）求证：平面平面。‎ 第19题图 ‎20.（本小题满分12分）‎ 如图，在四棱锥中，四边形是矩形，平面平面，点、分别为、中点，.三棱锥的体积. ‎ ‎（1）求证：平面； （2）求的长. ‎ ‎21.（本小题满分12分）‎ 如图1，在矩形中，，分别是的中点，分别是的中点。将四边形，分别沿，折起，使平面平面，平面平面，如图2所示。是上一点，且。‎ （1） 求证：；‎ （2） 线段上是否存在点，使得？若存在，求出的长，若不存在，请说明理由。‎ ‎22.（本小题满分12分） ‎ 已知圆，为圆内一点，为圆上的动点，且，是的中点。‎ （1） 求点的轨迹方程；‎ （2） 过点的直线与点的轨迹交于两点，求的取值范围。‎ 命题人：运城中学 淮冰会 运城中学、芮城中学 ‎2018-2019学年第一学期期中考试 高二数学评分标准（理）‎ 一、选择题(12*5=60分）‎ BCDBD DCCAA DC 二、填空题(4*5=20)‎ ‎13．－ ； 14．； 15．； 16．‎ 三、解答题(本大题共6小题,满分70分,解答须写出文字说明、证明过程或演算步骤.)‎ 17． ‎（10分）解：（1）由题得，..........................................1分 所以直线AB所在的直线方程为，即..........2分 联立 解得............................4分 所以顶点的坐标为（4,3）.....................5分 ‎（2）因为在直线上，所以设.....................6分 则，....................7分 代入中，得.....................8分 所以.....................9分 则直线的方程为，即....................10分 ‎18.（12分）解：（1）由，得中点为，，‎ 所以的垂直平分线为.....................2分 联立，得    ，则，....................4分 圆的半径为，...................5分 所以圆的方程为.....................6分 ‎（2）可以看成是点与连线的斜率.................7分 直线的方程为，即...................8分 当直线为圆的切线时，有，解得...................10分 所以的最大值为，最小值为 0....................12分 ‎19.（12分）证明：（1）取中点，连结，.…………………1分 ‎∵侧面是边长为的正三角形，∴。.…………………2分 在中，，，∴。.…………………3分 又，。.………………5分 且，∴..…………………6分 （2） 取中点，连结，，.……………7分 则，又∴..……………8分 确定一个平面，平面.………………9分 ‎，∴，.…………………10分 又∵，且，平面，.…………………11分 平面，‎ ‎∴平面平面.…………………12分 ‎20.（12分）（1）证明：取中点，连接．‎ 在△中，有，别为、中点，‎ ‎；……………………………………2分 在矩形中，为中点，‎ ‎，，四边形是平行四形，‎ ‎；………………………………………4分 而平面，平面，‎ 平面．………………………………………………6分 ‎（2）解：四边形是矩形，‎ ‎，；‎ 平面平面，平面平面，平面，‎ 平面，‎ 平面平面，平面，…………………………8分 ‎，设 ‎，，平面，‎ 平面，点到平面的距离．…………………………9分 三棱锥的体积 .…………………11分 解得，所以的长为2. .…………………12分 ‎21．（12分）‎ ‎（1）证明：由图（1）知，‎ 所以，又，‎ 所以。…………………………1分 因为，所以。…………………………2分 因为平面平面，平面平面，，所以。…………………………3分 所以。…………………4分 由（1）得，所以。‎ 在梯形中，易得，，所以。…………5分 ‎，所以。………………6分 ‎（2）当时，。…………………………7分 在上取点，使得，连结，‎ 所以。…………………8分 又，所以，‎ ‎，，………………………9分 是平行四边形，所以，…………………………10分 ‎。…………………………11分 此时。‎ 所以当时，。…………………………12分 ‎22.（12分）解：（1）设点，‎ 依题得，.…………………2分 即，.…………………3分 化简得。.…………………4分 ‎（2）设 ‎①当直线的斜率不存在时，其方程为，则 代入，得，则，‎ 所以此时。.…………………5分 ‎②当直线的斜率存在时，设其方程为，‎ 联立，得，‎ 则.…………………7分 ‎.……………8分 设，则。‎ 当时，；.…………………9分 当时，.…………………10分 ‎，‎ ‎。.…………………11分 综上所述。.…………………12分