北京市第十二中学2019-2020学年高一下学期五月测试选考物理试题 14页

北京市第十二中学2019-2020第二学期五月测试高一年级物理选考试卷 一、单项选择题 ‎1.以恒定功率行驶的汽车，若加速过程中受到的阻力不变，则牵引力F、加速度a和速度v的变化情况是（　　）‎ A. F、a、v均增大，最后达到稳定 B. F、v不断增大，a减小，最后做匀速运动 C. v不断变大，F、a变小，最后做匀速运动 D. F、a不变，v不断增大 ‎【答案】C ‎【解析】‎ ‎【详解】根据 可知，发动机的功率不变，汽车加速行驶的过程中，速度增大，则牵引力减小，根据 阻力不变，加速度减小，最后做匀速直线运动，故ABD错误，C正确。‎ 故选C。‎ ‎2.火星质量和半径分别约为地球的 和 ，地球表面的重力加速度为g，则火星表面的重力加速度约为(　　)‎ A. ‎0.2‎g‎ B. ‎0.4g C. ‎2.5g D. ‎‎5g ‎【答案】B ‎【解析】‎ 试题分析：根据星球表面的万有引力等于重力列出等式表示出重力加速度．‎ 通过火星的质量和半径与地球的关系找出重力加速度的关系．‎ 根据星球表面的万有引力等于重力知道 得出：‎ 火星的质量和半径分别约为地球的和 所以火星表面的重力加速度，故选B．‎ 考点：万有引力定律及其应用．‎ 点评：求一个物理量之比，我们应该把这个物理量先根据物理规律用已知的物理量表示出来，再进行之比．‎ ‎3.我国已成功发射多颗气象卫星，为气象预报提供了大量有效信息，其中“风云一号”是极地圆形轨道卫星，“风云二号”是地球同步卫星。且“风云一号”的运行周期是“风云二号”的一半，比较这两颗卫星，下列说法中正确的是（　　）‎ A. “风云一号”离地面较近，对同一区域连续观测时间长 B. “风云二号”离地面较近，观测覆盖区域大 C. “风云一号”运行线速度较大，观测覆盖区域大 D. “风云二号”运行线速度较大，对同一区域连续观测时间长 ‎【答案】C ‎【解析】‎ 详解】根据 得 ‎“风云一号”的周期小，则轨道半径小，所以“风云一号”离地面较近，而“风云二号”的周期大，则轨道半径大，则“风云二号”离地面较远。根据 得 ‎“风云一号”的轨道半径小，线速度大，“风云二号”轨道半径大，线速度小。由于地球自转，同步卫星（“风云二号”）与地球保持相对静止，所以同步卫星（“风云二号”）对同一区域连续观测时间长，极地卫星（“风云一号”）观测覆盖区域大，故ABD错误，C正确。‎ 故选C。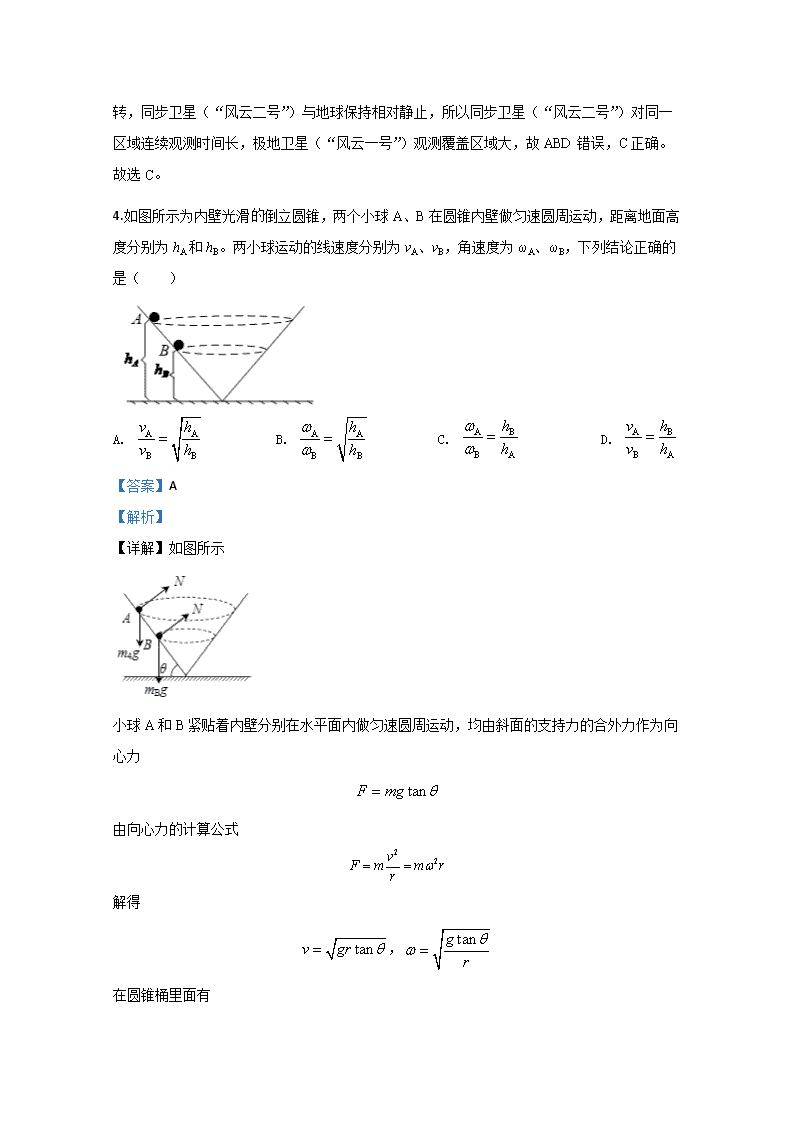‎ ‎4.如图所示为内壁光滑倒立圆锥，两个小球A、B在圆锥内壁做匀速圆周运动，距离地面高度分别为hA和hB。两小球运动的线速度分别为vA、vB，角速度为ωA、ωB，下列结论正确的是（　　）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【详解】如图所示 小球A和B紧贴着内壁分别在水平面内做匀速圆周运动，均由斜面的支持力的合外力作为向心力 由向心力的计算公式 解得 ‎，‎ 在圆锥桶里面有 故有 ‎，‎ 故A正确，BCD错误。‎ 故选A。‎ ‎5.向心力演示器如图所示转动手柄1，可使变速塔轮2和3以及长槽4和短槽5随之匀速转动皮带分别套在塔轮2和3上的不同圆盘上，可使两个槽内的小球分别以几种不同的角速度做匀速圆周运动小球做圆周运动的向心力由横臂6的挡板对小球的压力提供，球对挡板的反作用力，通过横臂的杠杆使弹簧测力套筒7下降，从而露出标尺8，标尺8上露出的红白相间等分格子的多少可以显示出两个球所受向心力的大小现将小球分别放在两边的槽内，为探究小球受到的向心力大小与角速度大小的关系，下列做法正确的是　　‎ A. 在小球运动半径相等的情况下，用质量相同的钢球做实验 B. 在小球运动半径相等的情况下，用质量不同的钢球做实验 C. 在小球运动半径不等的情况下，用质量不同的钢球做实验 D. 在小球运动半径不等的情况下，用质量相同的钢球做实验 ‎【答案】A ‎【解析】‎ 根据F＝mrω2，知要研究小球受到的向心力大小与角速度的关系，需控制小球的质量和半径不变．故A正确 故选A 点睛：明确本题目的，要研究小球受到的向心力和角速度的关系，则需要利用控制变量法去控制别的物理量不变，然后找向心力与角速度之间的关系．‎ ‎6.‎2017年10月16日，美国激光干涉引力波天文台等机构联合宣布首次发现双中子合并引力波事件。假设该事件中甲、乙两中子星的质量分别为m1、m2，它们绕其连线上的某点做圆周运动，且它们的间距在缓慢减小，不考虑其他星系的影响，则下列说法中正确的是（　　）‎ A. 甲、乙两中子星的角速度大小之比为m1∶m2‎ B. 甲乙两中子星的线速度大小之比为m2∶m1‎ C. 甲乙两中子星的运行周期不变 D. 甲、乙两中子星的向心加速度大小始终相等 ‎【答案】B ‎【解析】‎ ‎【详解】A．双星靠相互间的万有引力提供向心力，周期相等，角速度相等，所以角速度比1:2=1:1，故A错误；‎ B．双星靠相互间的万有引力提供向心力，角速度相等 m1r1ω2=m2r2ω2‎ 则半径 r1:r2=m2:m1‎ 根据v=ωr得 v1:v2=r1:r2=m2:m1‎ 故B正确；‎ C．根据 联立解得 由它们的间距在缓慢减小，则有甲乙两中子星的运行周期在减小，故C错误；‎ D．由a=rω2可知 a1:a2=r1:r2=m2:m1‎ 则甲、乙两中子星的向心加速度大小不相等，故D错误。‎ 故选B。‎ ‎7.按照我国月球探测活动计划，在第一步“绕月”工程圆满完成各项目标和科学探测任务后，第二步是“落月”工程，该计划已在2013年之前完成。设月球半径为R，飞船沿距月球表面高度为3R的圆形轨道Ⅰ运动，到达轨道的A点时点火变轨进入椭圆轨道Ⅱ，到达轨道的近月点B时再次点火进入月球近月轨道Ⅰ绕月球做圆周运动.卫星在轨道ⅠA处的速度为，加速度为；在轨道ⅡA处的速度为，加速度为；在轨道ⅡB处的速度为，加速度为；在轨道ⅢB处的速度为，加速度为。则它们大小关系正确的有（ ）‎ A. ， B. ，‎ C. ， D. ，‎ ‎【答案】B ‎【解析】‎ ‎【详解】A．飞船从轨道I上的A点要减速做向心运动进入轨道II，则有 由公式 可知 故A错误；‎ B．飞船从轨道II上的B点要减速做向心运动进入轨道III，则有 由公式 可知 故B正确；‎ C．飞船从轨道II上的A点运动到B点，由于万有引力做正功，则 且 故C错误；‎ D．由公式 可得 则有 由公式 可知 故D错误。‎ 故选B。‎ 二、多项选择题 ‎8.如图所示，绳子的一端固定在O点，另一端拴一重物在水平面上做匀速圆周运动（　　）‎ A. 转速相同时，绳长的容易断 B. 周期相同时，绳短的容易断 C. 线速度大小相等时，绳短的容易断 D. 角速度大小相等时，绳长的容易断 ‎【答案】ACD ‎【解析】‎ ‎【详解】A．根据牛顿第二定律得 m一定时，当转速n相同时，绳长r越长，绳子拉力F越大，绳子越容易断，故A正确；‎ B．根据牛顿第二定律得 m一定时，当周期T相同时，绳长r越长，绳子拉力F越大，绳子越容易断，故B错误；‎ C．根据牛顿第二定律得 m一定时，线速度大小相等时，绳长r越短，绳子拉力F越大，绳子越容易断，故C正确；‎ D．根据牛顿第二定律 m一定时，当角速度相等时，绳长r越长，绳子拉力F越大，绳子越容易断，故D正确。‎ 故选ACD。‎ ‎9.“和谐”号动车组列车高速运行时可以让乘客体验追风的感觉．我们把火车转弯近似看成是做匀速圆周运动，火车速度提高会使外轨受损．为解决火车高速转弯时不使外轨受损这一难题，你认为以下措施可行的是（　）‎ A. 增大弯道半径 B. 减小弯道半径 C. 增加内外轨的高度差 D. 减小内外轨的高度差 ‎【答案】AC ‎【解析】‎ ‎【详解】AB．设弯道半径为R，路面的倾角为θ，由牛顿第二定律得 θ一定，v增大时，可增大半径R，故A正确，B错误；‎ CD．根据 由于θ较小，则 h为内外轨道的高度差，L为路面的宽度．则 L、R一定，v增大，h增大，故C正确，D错误．‎ ‎10.如图所示，长为L的轻杆，一端固定一个小球，另一端固定在光滑的水平轴上，使小球在竖直平面内作圆周运动，关于小球在最高点的速度v0，下列说法中正确的是（　　）‎ A. v0的最小值为 B. v0由零逐渐增大，向心力也逐渐增大 C. 当v0由值逐渐增大时，杆对小球的弹力也逐渐增大 D. 当v0由值逐渐增小时，杆对小球的弹力也仍然逐渐增大 ‎【答案】BCD ‎【解析】‎ ‎【详解】A．由于杆子能支撑小球，故小球在最高点的最小速度为零，故A错误；‎ B．小球的向心力为 则v0由零逐渐增大，向心力也逐渐增大，故B正确；‎ C．在最高点，杆子对小球的作用力为零时，有 解得 当 时杆子表现为拉力，根据牛顿第二定律有 即速度增大时，杆对小球的弹力逐渐增大，故C正确；‎ D．当 时杆子表现为支持力，根据牛顿第二定律有 即速度减小，杆对小球的弹力逐渐增大，故D正确。‎ 故选BCD。‎ 三、填空题 ‎11.质量为‎10kg的小球，从高处自由下落，则前2s内重力的平均功率______W，第2s末的功率______W。（g取‎10m/s2）‎ ‎【答案】 (1). 1000 (2). 2000‎ ‎【解析】‎ ‎【详解】由 可得 重力做的功为 则前2s内重力的平均功率为 落地时速度为 第2s末的功率为 ‎12.用50N的力拉一个质量为‎10kg的物体在水平地面上前进，如图所示。若物体前进了‎10m，拉力F做的功为______J。如果物体与水平面间动摩擦因数μ=0.1，物体克服阻力做功为___________J。（sin37°=0.6，cos37°=0.8）‎ ‎【答案】 (1). 400 (2). 70‎ ‎【解析】‎ ‎【详解】根据 得拉力F做的功为 如下图所示，物体受重力、支持力、拉力和摩擦力 则支持力大小为 摩擦力的大小为 故物体克服阻力做功为 ‎13.两颗人造地球卫星的质量之比mA:mB=2:1，轨道半径之比RA:RB=3:1，那么，它们的周期之比TA:TB=______，它们所受向心力之比FA:FB=______。‎ ‎【答案】 (1). (2). ‎ ‎【解析】‎ ‎【详解】根据万有引力提供向心力，有 得 因轨道半径之比 则他们的周期之比为 又因质量之比为 故它们所受向心力之比为 四、计算题 ‎14.如图所示，质量m＝‎800kg的汽车以不变的速率先后驶过凹形桥面和凸形桥面，两桥面的圆弧半径均为‎50 m．当小汽车通过凹形桥面最低点时对桥面的压力为8400N，则：‎ ‎(1)汽车的运行速率是多少？‎ ‎(2)若以所求速度行驶，汽车对凸形桥面最高点的压力是多少？(g取‎10 m/s2)‎ ‎【答案】(1) ‎5m/s (2) 7600N ‎【解析】‎ ‎【详解】（1）汽车在最低点受到的支持力最大，此时速度最大，根据牛顿第二定律得：‎ 代入数据得 ‎(2)当汽车运动到最高点时，支持力最小，根据牛顿第二定律得：‎ 代入数据得N.‎ ‎15.恒星演化发展到一定阶段，可能成为恒星世界的“侏儒”-中子星，中子星的半径较小，一般在7~‎20km，但它的密度大得惊人。若中子星的半径为‎10km，密度为1.2×‎1017kg/m3。已知万有引力常量G=6.67´10-11N m2/kg2，那么该中子星的第一宇宙速度约为多少？（计算结果保留一位有效数字）‎ ‎【答案】‎ ‎【解析】‎ ‎【详解】中子星上的第一宇宙速度即为它表面处的卫星的环绕速度，此时卫星的轨道半径可近似认为是该中子星的半径，且中子星对卫星的万有引力充当向心力，由 得 又 联立解得该中子星的第一宇宙速度约为 ‎16.‎2018年12月8日凌晨，我国在西昌卫星发射中心利用长征三号乙改进型运载火箭成功发射嫦娥四号探测器，对月球背面南极艾特肯盆地开展着陆巡视探测，实现了人类首次月球背面软着陆和巡视勘察。假设探测器在近月轨道上绕月球做匀速圆周运动，经过时间t（小于绕行周期）运动的弧长为s，探测器与月球中心连线扫过的角度为（弧度），引力常量为G，求：‎ ‎(1)探测器的轨道半径；‎ ‎(2)探测器的环绕周期；‎ ‎(3)月球的质量。‎ ‎【答案】(1)；(2)；(3)‎ ‎【解析】‎ ‎【详解】(1)根据几何关系得探测器的轨道半径为 ‎(2)经过时间t（小于绕行周期）运动的弧长为s，探测器与月球中心连线扫过的角度为（弧度），由 得探测器的环绕周期为 ‎(3)由万有引力充当向心力得 解得月球的质量为