- 1.50 MB
- 2021-05-06 发布
(四川省阆中中学2020届高三)2020年普通高等学校招生全国统一考试适应性考试(二)数学(理)试题
一. 选择题(每题5分,共60分)
1. 已知集合A={1, 2, 3, 4, 5},B={(x,y)| x∈A, y∈A, x-y∈A},则B中所含元素的个数为( )
A. 3 B. 6 C. 8 D. 10
2. 设复数z满足,z在复平面内对应的点为(x,y),则( )
A. B.
C. D.
3. 已知向量,且,则m =( )
A.8 B.6 C.-6 D.-8
4.已知双曲线,其焦点到的一条渐近线的距离为2,该双曲线的离
心率为
A. B. C. D.
5.我国古代数学著作(算法统宗》中有这样一个问题(意为):“有一个人要走378里路,第
一天健步行走,从第二天起因脚痛每天走的路程为前一天的一半,走了6天后到达目的
地.“那么,此人第4天和第5天共走路程是
A.24里 B.36里 C.48里 D.60里
6. 安排3名志愿者完成4项工作,每人至少完成1项,每项工作由1人完成,则不同的
安排方式共有( )
A.12种 B.18种 C.24种 D.36种
7.已知满足,则( )
A. B. C. D.
8.已知 则a,b,c的大小关系为( )
A. B. C. D.
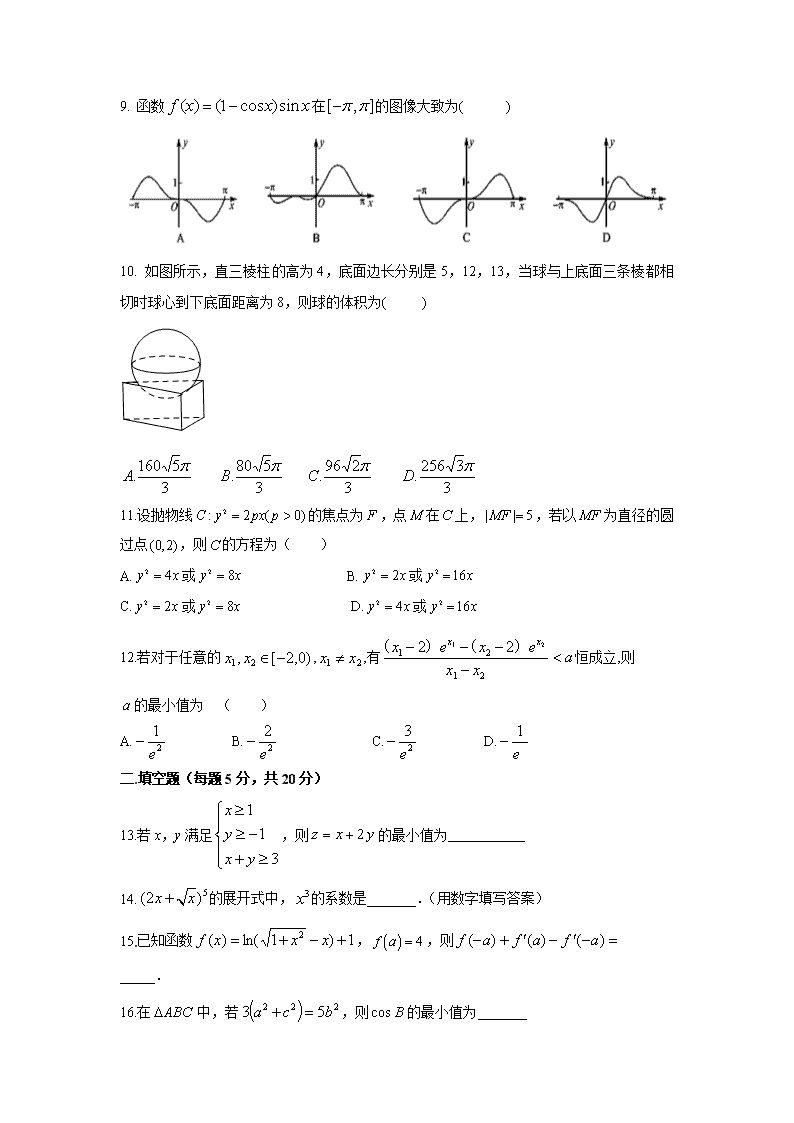
9. 函数在的图像大致为( )
10. 如图所示,直三棱柱的高为4,底面边长分别是5,12,13,当球与上底面三条棱都相切时球心到下底面距离为8,则球的体积为( )
11.设抛物线的焦点为,点在上,,若以为直径的圆
过点,则的方程为( )
A.或 B.或
C.或 D.或
12.若对于任意的,,有恒成立,则
的最小值为 ( )
A. B. C. D.
二.填空题(每题5分,共20分)
13.若x,y满足,则的最小值为
14.的展开式中,的系数是_______.(用数字填写答案)
15.已知函数,,则
_____.
16.在中,若,则的最小值为
三、解答题(共70分,解答题应写出文字说明,证明过程或演算步骤)
17.(本题满分12分)设等差数列的前项和为,数列是等比数列,
,,.
(1)求数列和 的通项公式;
(2)设, 求数列的前项和.
18.(本题满分12分)在某单位的食堂中,食堂每天以10元/斤的价格购进米粉,然后
以4.4元/碗的价格出售,每碗内含米粉0.2斤,如果当天卖不完,剩下的米粉以2元/斤的价格卖给养猪场.根据以往统计资料,得到食堂某天米粉需求量的频率分布直方图如图所示,若食堂购进了80斤米粉,以(斤)(其中)表示米粉的需求量,(元)表示利润.
(1)估计该天食堂利润不少于760元的概率;
(2)在直方图的需求量分组中,以区间中间值作为该区间的需求量,以需求量落入该区
间的频率作为需求量在该区间的概率,求 的分布列和数学期望.
19.(本题满分12分)如图所示,直三棱柱 的各棱长均相等,点为
的中点.
(1)证明:;
(2)求二面角 的余弦值.
20.(本题满分12分)己知圆F1:(x+1)2 +y2= r2(1≤r≤3),圆F2:(x-1)2+y2= (4-r)2 .
(1)证明:圆F1与圆F2有公共点,并求公共点的轨迹E的方程;
(2)已知点Q(m,0)(m<0),过点且斜率为k(k≠0)的直线与(Ⅰ)中轨迹E相交
于M,N两点,记直线QM的斜率为,直线QN的斜率为, 是否存在实数
使得为定值?若存在,求出的值,若不存在,说明理由.
21.(本题满分12分)已知函数f(x)=2sinx-xcosx-x,为的导数.
(1)证明:在区间存在唯一零点;
(2)若x∈[0,π]时,f(x)≥ax,求a的取值范围.
请考生在第22,23三题中任选一题作答,如果多做,则按所做的第一题得分.作答时请写清题号
22.(本题满分10分)在平面直角坐标系中,的参数方程为(t为参数).以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为.
(1)求的普通方程和曲线C的直角坐标方程;
(2)求曲线C上的点到 距离的最大值及该点坐标.
23.(本题满分10分)设函数.
(Ⅰ)求不等式的解集;
(Ⅱ)若关于的不等式有解,求实数的取值范围.
参考答案
一、请将选择答案填入下列表格(每小题5分,共计60分)
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
D
C
A
B
B
D
A
B
C
A
D
C
二、 请将填空题答案填入下列横线(每小题5分,共计20分)
13.2 14.10 15. -2 16.
三、 解答题(本大题共6小题,共70分,解答应写出文字说明,证明过程,或演算步骤)
17. (1)解:设等差数列 的公差为 ,等比数列 的公比为 .
,即 ,
..........................................................................................................2分
, , ......................................3分
. , , ............................6分
(2)解: .............................8分
...........................................10分
.....12分
18. (1)解:一斤米粉的售价是 元.
当 时, .
当 时, .
故 ............................................................................3分
设利润 不少于760元为事件 ,
利润 不少于760元时,即 .
解得 ,即 .
由直方图可知,当 时,
.........................................................5分
(2)解:当 时, ;
当 时, ;
当 时, ;
当 时,
所以 可能的取值为460,660,860,960.........................................................9分
,
,
,
.
故 的分布列为
........................................................................10分
................................12分
19.(1)证明:设 与 交点为 ,连接 , . 由题可知四边形 为正方形,所以 ,且 为 中点.
又因 , ,
所以 ,所以 .
又因为 ,所以 平面 .
因为 平面 ,所以 ....................5分
(2)解:取 的中点 ,连接 , ,在平面 过点 内作 的垂线,如图所示,建立空间直角坐标系 .
设 ,则 , , , .
所以 , .......................................................................7分
设平面 的一个法向量为 ,
则 ,令 ,则 ................9分
由(1)可知平面 的一个法向量为 ,.............................10分
则
由图可知二面角 为锐角,所以其余弦值为 ......................................12分
20. (1)证明:因为 , ,所以 ,
因为圆 的半径为 ,圆 的半径为 ,......................................................1分
又因为 ,所以 ,即 ,
所以圆 与圆 有公共点,.........................................................................................2分
设公共点为 ,因此 ,所以 点的轨迹 是以 , 为焦点的椭圆,所以 , , ,....................................4分
即轨迹 的方程为 ..........................................................................................5分
(2)解:过 点且斜率为 的直线方程为 ,设 ,
由 消去 得到 ,
则 , , ① ...............................................................7分
因为 , ,
所以
,
将①式代入整理得 ...................................................10分
因为 ,
所以当 时,即 时, .
即存在实数 使得 ..............................................................12分
21.解:(1)设,则..........1分
当时,;当时,,
所以在单调递增,在单调递减...........................................3分
又,故在存在唯一零点.............4分
所以在存在唯一零点.......................................................................5分
(2)由题设知f(x)≥ax ,则解得a≤0..............................................6分
现在只要说明a≤0符合题意
由(1)知,在只有一个零点,设为,
且当时,当时,,
所以在单调递增,在单调递减...........................................8分
又,所以,当时,f(x)≥0................................10分
又当时,ax≤0,故...............................................................11分
因此,a的取值范围是.........................................................................................12分
22.(1)解:由 (t为参数),得 .
消去参数t , 得 的普通方程为 ;..........................................3分
将 去分母得 ,将 代入,得
所以曲线C的直角坐标方程为 ..................................................5分
(2)解:由(1)可设曲线C的参数方程为 ( 为参数),......................6分
则曲线C上的点到 的距离
,..................................................7分
当 ,即 时,.......................................8分
,....................................................................9分
此时, ,...................................................................10分
所以曲线C上的点到直线 距离的最大值为 ,该点坐标为 .......................10分
23. 解:(Ⅰ) ,..........................................................2分
当 时, ,解得 ,所以 ;
当 时, ,解得 ;
当 时, ,解得 ,所以 ,...............................................4分
综上所述,不等式 的解集为 或 ..............................5分
(Ⅱ)∵
(当且仅当 即 时取等).................................................7分
∴ .....................................................10分