2021届课标版高考文科数学大一轮复习课件：§7-1 不等式的概念及性质、一元二次不等式（讲解部分） 18页

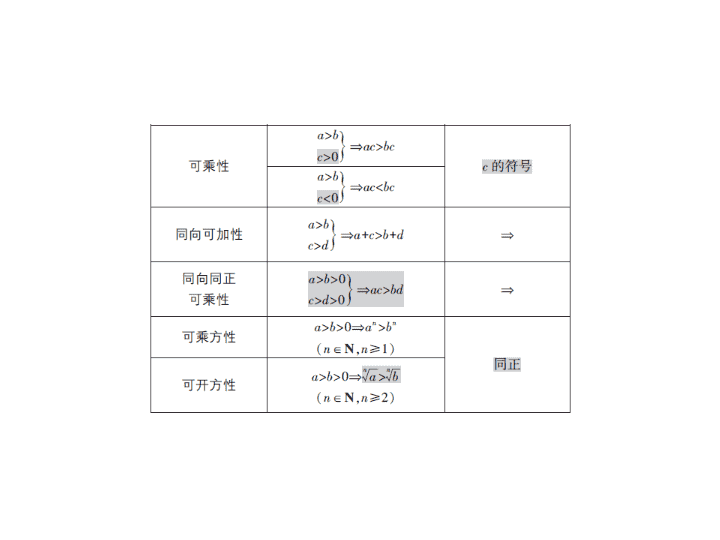
专题七　不等式 §7.1 　不等式的概念及性质、一元二次不等式 高考文数 考点一　不等式的概念及性质 考点清单 考向基础 1.不等式的基本性质 2.不等式的倒数和分数性质 (1)倒数性质: a > b , ab >0 ⇒   <   ; a <0< b ⇒   <   . (2)有关分数的性质:若 a > b >0, m >0,则   <   ;   >   ( b - m >0);   >   ;   <   ( b - m >0). 考向　利用不等式性质比较大小 考向突破 例1　若 a , b 为非零实数,且 a < b ,则下列判断正确的是   (　　) A. a 2 < b 2 　     B. a 2 b < ab 2 C.   <   　    D.   <   解析　对于选项A,取 a =-3, b =1,则 a 2 < b 2 不成立;对于选项B,当 ab <0时, ab ( a - b )>0,即 a 2 b > ab 2 ;对于选项C,∵ a , b 为非零实数,且 a < b ,∴   <   ,化简得   <   ;对于选项D,取 a =-2, b =1,则   >   .故选C. 答案    C 考点二　一元二次不等式 考向基础 1.一元二次不等式与相应的二次函数及一元二次方程的关系 在不等式 ax 2 + bx + c >0( a ≠ 0)中,如果二次项系数 a <0,则可先根据不等式 的性质,将二次项系数转化为正数,再对照上表求解. 2.含参一元二次不等式的解法 (1)若二次项含有参数,则应先讨论参数是等于0,小于0,还是大于0,然后整 理不等式. (2)当二次项系数不为0时,讨论判别式 Δ 与0的关系,判断相应一元二次方程 的根的个数. (3)确定无根时直接写出解集,确定方程有两个实根时,要讨论两根的大小 关系,从而确定解集的形式. 【知识拓展】 分式不等式的解法: (1)   >0(<0) ⇔ f ( x )· g ( x )>0(<0); (2)   ≥ 0( ≤ 0) ⇔   考向一　求含参不等式的解集 考向突破 例2　求关于 x 的不等式 ax 2 -2 ≥ 2 x - ax ( a ∈R)的解集. 解析　原不等式变形为 ax 2 +( a -2) x -2 ≥ 0. ①当 a =0时, x ≤ -1. ②当 a ≠ 0时,不等式即为( ax -2)( x +1) ≥ 0. 当 a >0时, x ≥   或 x ≤ -1. 当 a <0时,由于   -(-1)=   , 于是,当-2< a <0时,   ≤ x ≤ -1; 当 a =-2时, x =-1; 当 a <-2时,-1 ≤ x ≤   . 综上所述,当 a =0时,不等式的解集为{ x | x ≤ -1};当 a >0时,不等式的解集为   ;当-2< a <0时,不等式的解集为   ;当 a =-2时,不等 式的解集为{ x | x =-1};当 a <-2时,不等式的解集为   . 考向二　不等式恒成立,求参数范围 例3    (2018黑龙江大庆实验中学期中,5)对于任意实数 x ,不等式( a -2) x 2 -2( a - 2) x -4<0恒成立,则实数 a 的取值范围是(　　) A.(- ∞ ,2)　    B.(- ∞ ,2]　    C.(-2,2)　    D.(-2,2] 解析　当 a -2=0,即 a =2时,-4<0恒成立; 当 a -2 ≠ 0,即 a ≠ 2时, 则有   解得-2< a <2. 综上,实数 a 的取值范围是(-2,2].故选D. 答案    D 方法1 　比较大小的常用方法 1. 构造函数 ,判断出函数的单调性,让所要比较大小的数在同一单调区间内, 然后利用单调性进行比较. 2. 作差 ,与0比较,即 a - b >0 ⇔ a > b ; a - b =0 ⇔ a = b ; a - b <0 ⇔ a < b . 3. 作商 ,与1比较,即   >1, b >0 ⇔ a > b ;   =1, b ≠ 0 ⇔ a = b ;   <1, b >0 ⇔ a < b . 方法技巧 例1　已知实数 a =   , b =   , c =   ,则 a , b , c 的大小关系为   (　　) A. a < b < c 　    B. c < a < b C. c < b < a 　    D. b < a < c 解析　解法一:(作差法) a - b =   -   =   =   >0,∴ a > b . c - a =   -   =   =   <0,∴ c < a . b - c =   -   =   =   >0,∴ b > c . ∴ a > b > c ,故选C. 解法二:(单调性法)由式子结构可设 f ( x )=   ,则 f '( x )=   ,令 f '( x )=0,得 x =e, 则 x ∈(0,e)时, f '( x )>0, f ( x )单调递增; x ∈(e,+ ∞ )时, f '( x )<0, f ( x )单调递减. 又∵3,4,5∈(e,+ ∞ ),∴ f (3)> f (4)> f (5), ∴   >   >   ,即 a > b > c . 答案    C 方法2　 一元二次不等式恒成立问题的解法 1.函数法 设 f ( x )= ax 2 + bx + c ( a ≠ 0). (1) f ( x )>0在 x ∈R上恒成立 ⇔ a >0且 Δ <0 ; (2) f ( x )<0在 x ∈R上恒成立 ⇔ a <0且 Δ <0 ; (3)当 a >0时, f ( x )>0在 x ∈[ α , β ]上恒成立 ⇔   或   或   f ( x )<0在 x ∈[ α , β ]上恒成立 ⇔   (4)当 a <0时, f ( x )>0在 x ∈[ α , β ]上恒成立 ⇔   f ( x )<0在 x ∈[ α , β ]上恒成 立 ⇔   或   或   2.最值法 对于含参数的不等式恒成立问题,常通过分离参数,把求参数的范围问题转 化为求函数的最值问题. a > f ( x )恒成立 ⇔ a > f ( x ) max ; a < f ( x )恒成立 ⇔ a < f ( x ) min . 注意:解决恒成立问题一定要清楚选谁为主元,谁是参数.一般地,知道谁的 范围,就选谁当主元,求谁的范围,谁就是参数. 例2    (2018豫西南五校联考,7)已知关于 x 的不等式 kx 2 -6 kx + k +8 ≥ 0对任意 x ∈R恒成立,则 k 的取值范围是(　　) A.0 ≤ k ≤ 1　     B.0< k ≤ 1 C. k <0或 k >1　    D. k ≤ 0或 k ≥ 1 解析　当 k =0时,不等式 kx 2 -6 kx + k +8 ≥ 0可化为8 ≥ 0,恒成立;当 k ≠ 0时,要满 足关于 x 的不等式 kx 2 -6 kx + k +8 ≥ 0对任意 x ∈R恒成立, 只需   解得0< k ≤ 1. 综上, k 的取值范围是0 ≤ k ≤ 1.故选A. 答案    A