2013届人教A版理科数学课时试题及解析（50）抛物线B 4页

课时作业(五十)B　[第50讲　抛物线]‎ ‎[时间：35分钟　　分值：80分]‎ ‎1．若点P(x，y)到点F(0,2)的距离比它到直线y＋4＝0的距离小2，则P(x，y)的轨迹方程为(　　)‎ A．y2＝8x B．y2＝－8x C．x2＝8y D．x2＝－8y ‎2．抛物线x2＝(‎2a－1)y的准线方程是y＝1，则实数a＝(　　)‎ A. B. C．－ D．－ ‎3．已知抛物线y2＝4x，若过焦点F且垂直于对称轴的直线与抛物线交于A，B两点，O是坐标原点，则△OAB的面积是(　　)‎ A．1 B．‎2 C．4 D．6‎ ‎4．对于抛物线y2＝4x上任意一点Q，点P(a,0)都满足|PQ|≥|a|，则a的取值范围是(　　)‎ A．(－∞，0) B．(－∞，2]‎ C．[0,2] D．(0,2)‎ ‎5．已知A，B是抛物线y2＝2px(p>0)上的两点，O是原点，若|OA|＝|OB|，且△AOB的垂心恰好是抛物线的焦点，则直线AB的方程是(　　)‎ A．x＝p B．x＝3p C．x＝p D．x＝p ‎6．已知抛物线y2＝2px(p>0)的焦点为F，点P1(x1，y1)，P2(x2，y2)，P3(x3，y3)均在抛物线上，且2x2＝x1＋x3，则有(　　)‎ A．|FP1|＋|FP2|＝|FP3|‎ B．|FP1|2＋|FP2|2＝|FP3|2‎ C．2|FP2|＝|FP1|＋|FP3|‎ D．|FP2|2＝|FP1|·|FP3|‎ ‎7．已知点P是抛物线y2＝2x上的一个动点，则点P到点(0,2)的距离与P到该抛物线准线的距离之和的最小值为(　　)‎ A. B．‎3 C. D. 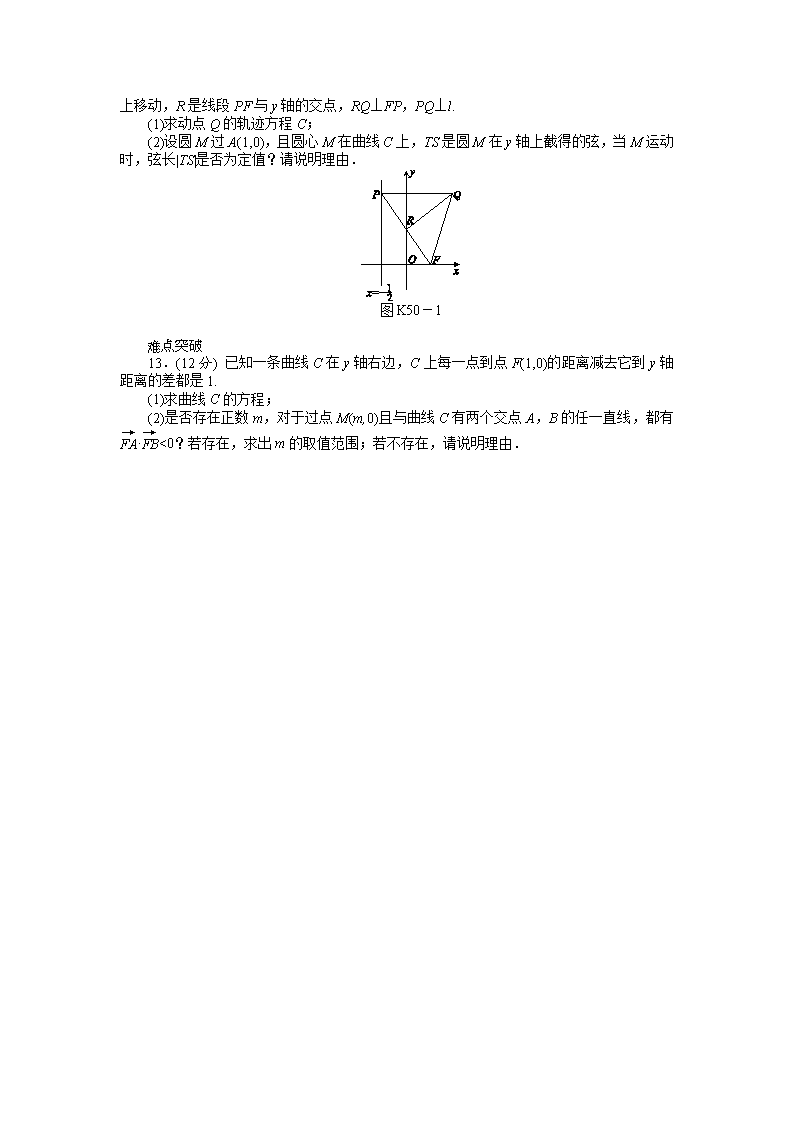‎8． 若抛物线y2＝4x的焦点是F，准线是l，点M(4,4)是抛物线上一点，则经过点F、M且与l相切的圆共有(　　)‎ A．0个 B．1个 C．2个 D．4个 ‎9．已知抛物线C的顶点坐标为原点，焦点在x轴上，直线y＝x与抛物线C交于A，B两点，若P(2,2)为AB的中点，则抛物线C的方程为________．‎ ‎10． 已知抛物线C：y2＝2px(p＞0)的准线为l，过M(1,0)且斜率为的直线与l相交于点A，与C的一个交点为B.若＝，则p＝________.‎ ‎11． 已知以F为焦点的抛物线y2＝4x上的两点A、B满足＝3，则弦AB的中点P到准线的距离为________．‎ ‎12．(13分) 在平面直角坐标系xOy中，设点F，直线l：x＝－，点P在直线l上移动，R是线段PF与y轴的交点，RQ⊥FP，PQ⊥l.‎ ‎(1)求动点Q的轨迹方程C；‎ ‎(2)设圆M过A(1,0)，且圆心M在曲线C上，TS是圆M在y轴上截得的弦，当M 运动时，弦长|TS|是否为定值？请说明理由．‎ 图K50－1‎ ‎13．(12分) 已知一条曲线C在y轴右边，C上每一点到点F(1,0)的距离减去它到y轴距离的差都是1.‎ ‎(1)求曲线C的方程；‎ ‎(2)是否存在正数m，对于过点M(m,0)且与曲线C有两个交点A，B的任一直线，都有·<0？若存在，求出m的取值范围；若不存在，请说明理由．‎ 课时作业(五十)B ‎【基础热身】‎ ‎1．C　[解析] 点P(x，y)到点F(0,2)的距离比它到直线y＋4＝0的距离小2，说明点P(x，y)到点F(0,2)的距离与到直线y＋2＝0即y＝－2的距离相等，轨迹为抛物线，其中p＝4，故所求的抛物线方程为x2＝8y.‎ ‎2．D　[解析] 根据分析把抛物线方程化为x2＝－2y，则焦参数p＝－a，故抛物线的准线方程是y＝＝，则＝1，解得a＝－.‎ ‎3．B　[解析] 焦点坐标是(1,0)，A(1,2)，B(1，－2)，|AB|＝4，故△OAB的面积S＝|AB||OF|＝×4×1＝2.‎ ‎4．B　[解析] 设点Q的坐标为，由|PQ|≥|a|，得y＋2≥a2，整理，得y(y＋16－‎8a)≥0，∵y≥0，∴y＋16－‎8a≥0，即a≤2＋恒成立．而2＋的最小值为2，所以a≤2.‎ ‎【能力提升】‎ ‎5．D　[解析] A(x0，y0)，则B(x0，－y0)，由于焦点F，0是抛物线的垂心，所以OA⊥BF.由此得×＝－1，把y＝2px0代入得x0＝，故直线AB的方程是x＝p.‎ ‎6．C　[解析] 由抛物线定义，2＝＋，即2|FP2|＝|FP1|＋|FP3|.‎ ‎7．A　[解析] 依题设P在抛物线准线的投影为P′，抛物线的焦点为F，则F.依抛物线的定义知P到该抛物线准线的距离为|PP′|＝|PF|，则点P到点A(0,2)的距离与P到该抛物线准线的距离之和d＝|PF|＋|PA|≥|AF|＝＝.‎ ‎8．C　[解析] 满足条件的圆的圆心C到F的距离到准线l的距离相等，故圆心C一定在抛物线上，又需满足|CM|＝|CF|，故点C在线段MF的垂直平分线l′上，而l′与抛物线有两个交点C1，C2，则分别以C1，C2为圆心，|C‎1F|，|C‎2F|为半径的两个圆都符合要求．‎ ‎9．y2＝4x　[解析] 设抛物线方程为y2＝kx，与y＝x联立方程组，消去y，得：x2－kx＝0，x1＋x2＝k＝2×2＝4，故y2＝4x.‎ ‎10．2　[解析] 过B作BE垂直于准线l于E，∵＝，∴M为AB中点，∴|BM|＝|AB|.又斜率为，∠BAE＝30°，∴|BE|＝|AB|，∴|BM|＝|BE|，‎ ‎∴M为抛物线的焦点，∴p＝2.‎ ‎11.　[解析] 设A(xA，yA)，B(xB，yB)，则|AF|＝xA＋1，|BF|＝xB＋1，∴xA＋1＝3(xB＋1)．①‎ 由几何关系，xA－1＝3(1－xB)．②‎ 联立①②，得xA＝3，xB＝，∴所求距离d＝＋1＝.‎ ‎12．[解答] (1)依题意知，‎ 点R是线段FP的中点，且RQ⊥FP，‎ ‎∴RQ是线段FP的垂直平分线．‎ ‎∵|PQ|是点Q到直线l的距离．‎ 点Q在线段FP的垂直平分线上，∴|PQ|＝|QF|.‎ 故动点Q的轨迹是以F为焦点，l为准线的抛物线，‎ 其方程为：y2＝2x(x>0)．‎ ‎(2)弦长|TS|为定值．理由如下：取曲线C上点M(x0，y0)，M到y轴的距离为d＝|x0|＝x0，‎ 圆的半径r＝|MA|＝，‎ 则|TS|＝2＝2，‎ 因为点M在曲线C上，所以x0＝，‎ 所以|TS|＝2＝2，是定值．‎ ‎【难点突破】‎ ‎13．[解答] (1)设P(x，y)是曲线C上任意一点，那么点P(x，y)满足－x＝1(x>0)．‎ 化简得y2＝4x(x>0)．‎ ‎(2)设过点M(m,0)(m>0)的直线l与曲线C的交点为A(x1，y1)，B(x2，y2)．‎ 设l的方程为x＝ty＋m，由得y2－4ty－‎4m＝0，Δ＝16(t2＋m)>0，‎ 于是①‎ 又＝(x1－1，y1)，＝(x2－1，y2)，‎ ·<0⇔(x1－1)(x2－1)＋y1y2＝x1x2－(x1＋x2)＋1＋y1y2<0.②‎ 又x＝，于是不等式②等价于·＋y1y2－＋1<0，‎ ‎⇔＋y1y2－[(y1＋y2)2－2y1y2]＋1<0.③‎ 由①式，不等式③等价于m2－‎6m＋1<4t2.④‎ 对任意实数t,4t2的最小值为0，所以不等式④对于一切t成立等价于m2－‎6m＋1<0，即3－2