2017-2018学年广东省江门市第二中学高二下学期3月月考数学（文）试题 Word版 7页

2017-2018 学年广东省江门市第二中学高二下学期 3 月月考 数学试卷（文科） 参考公式： ；a^ ＝ y － －b^ x － ；y^ ＝b^ x＋a^ . 注意事项：本试卷共 页，22 小题，满分 ，考试用时 分钟。 一、选择题：(本大题共 12 小题，每小题 分，满分 60 分，在每小题给出的四个选项中，只 有一项是符合题目要求的。) 1. 若复数 ，则 在复平面内对应的点位于 A．第一象限 B．第二象限 C．第三象限 D．第四象限 2. 点 M 的极坐标是（ ），则点 M 的直角坐标为 A．（ ， ） B．（ ， ） C．（ ， ） D．以上都不对 3. 通过随机询问 110 名性别不同的大学生是否爱好某项运动，得到如下的列联表： 男 女 合计 爱好 40 20 60 不爱好 20 30 50 总计 60 50 110 由 K2＝ n(ad－bc)2 (a＋b)(c＋d)(a＋c)(b＋d)，得 K2＝110 × (40 × 30－20 × 20)2 60 × 50 × 60 × 50 ≈7.8. 附表： 参照附表，得到的正确的结论是 A．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别有关” B．在犯错误的概率不超过 0.1%的前提下，认为“爱好该项运动与性别无关” C．有 99%以上的把握认为“爱好该项运动与性别有关” D．有 99%以上的把握认为“爱好该项运动与性别无关” 4.若散点图所有样本点都在一条直线上，则解释变量和预报变量之间的相关指数 是 A．1 B．-1 C．0 D．2 5. 曲线 y＝x3－2x＋1 在点（1,0）处的切线方程为 A．y＝x－1 B．y＝－x＋1 C．y＝2x－2 D．y＝－2x＋2 6．下列表述正确的是 ①归纳推理是由部分到整体的推理；②归纳推理是由一般到一般的推理； ③演绎推理是由一般到特殊的推理；④类比推理是由特殊到一般的推理； ⑤类比推理是由特殊到特殊的推理。 A．①②③；　　B．②③④； 　C．②④⑤；　D．①③⑤ 7. 执行如右图所示的程序框图．如果输入 n＝3，则输出的 S＝ A．6 7 B．3 7 C．8 9 D．4 9 P(K2≥k) 0.050 0.010 0.001 k 3.841 6.635 10.828 ∑ ∑ = = ∧ − ⋅− = n i i n i ii xnx yxnyx b 1 22 1 4 150 120 5 iz −= 1 z 6,3 π 2 33 2 3 2 3 2 3 2 3 2 33 2R 8. 用反证法证明：三角形三个内角至少有一个不大于 60°时，应假设 A．三个内角都不大于 60° B．三个内角至多有一个大于 60° C．三个内角都大于 60° D．三个内角至多有两个大于 60° 9. 三角形的面积为 ，a、b、c 为三角形的边长， r 为三角形内切圆的半径，类比推理可以得到四面体的体积为 A． B． C． （ 分别为四面体的四个面的面积，r 为四 面体的内切球的半径） D． （h 为四面体的高） 10．用火柴棒摆“金鱼”，如图所示：按照上面的规律，第 n 个“金鱼”图形需要火柴棒的 根数为 A．6n－2 B．8n－2 C．6n＋2 D．8n＋2 11. 极坐标方程 表示的图形是 A．两个圆 B．一个圆和一条直线 C．一个圆和一条射线 D．一条直线和一条射线 12. 函数 的图象如图所 示，则下列结论成立的是 A．a>0，b<0，c>0，d>0 B．a>0，b<0，c<0，d>0 C．a<0，b<0，c>0，d>0 D．a>0，b>0，c>0，d<0 二、填空题：(本大题共 小题，每小题 分，满分 分。) 13. 已知复数 z 满足2－i z ＝1＋2i，则z＝ 。 14．在极坐标系中，点 到直线 的距离是 。 15．已知 x 与 y 之间的数据如下，则 y 与 x 的线性回归方程为 y=bx+a，必过点 。 x 0 1 2 3 y 1 3 5 7 16. 依次有下列等式： ，按此规律下去，第 5 个等 式为 。 x 0 1 2 3 y 1 3 5 7 rcbas ⋅++= )(2 1 abcV 3 1= shV 3 1= rssssV ⋅+++= )(3 1 4321 4321 ssss 、、、 hacbcabV ⋅++= )(3 1 ( )( ) ( )1 0 0ρ θ ρ− − = ≥π ， dcxbxaxxf +++= 23)( 4 5 20 (2, )6 π sin( ) 16 πρ θ − = 222 576543,3432,11 =++++=++= 三、解答题：（本大题共 6 小题，满分 70 分。解答须写出文字说明，步骤。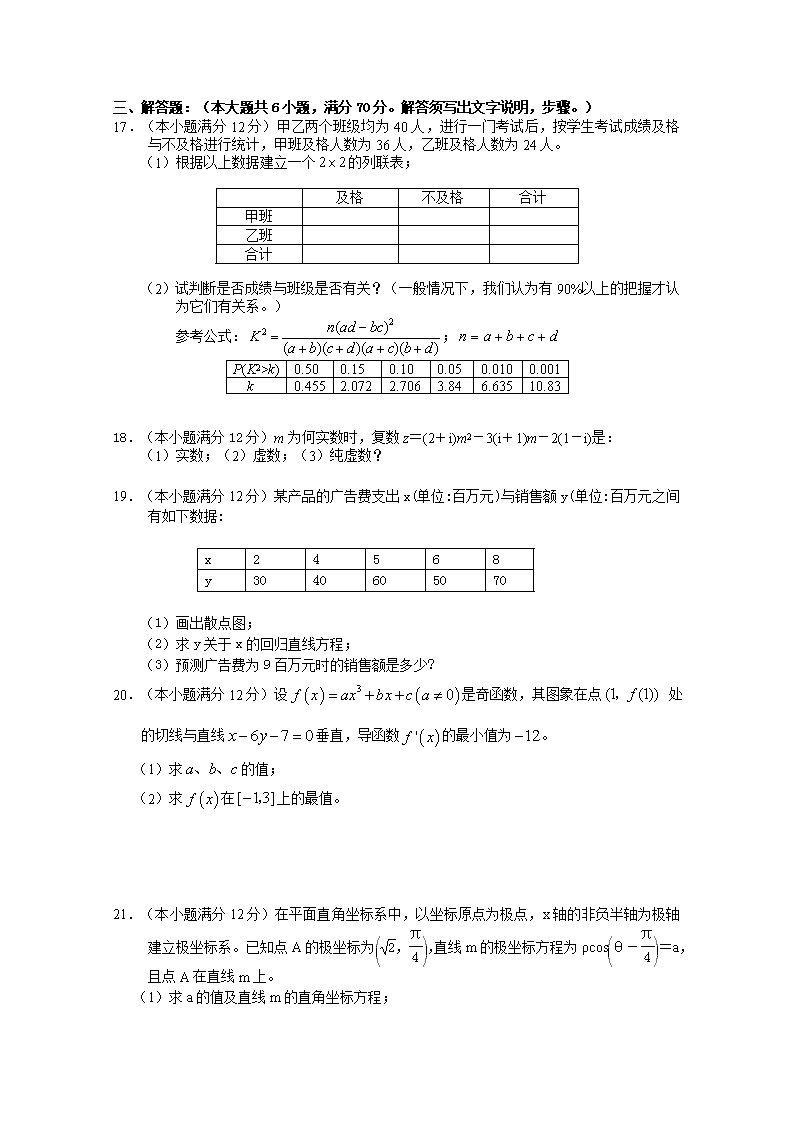） 17．（本小题满分 12 分）甲乙两个班级均为 40 人，进行一门考试后，按学生考试成绩及格 与不及格进行统计，甲班及格人数为 36 人，乙班及格人数为 24 人。 （1）根据以上数据建立一个 的列联表； 及格 不及格 合计 甲班 乙班 合计 （2）试判断是否成绩与班级是否有关？（一般情况下，我们认为有 90%以上的把握才认 为它们有关系。） 参考公式： ； P(K2>k) 0.50 0.15 0.10 0.05 0.010 0.001 k 0.455 2.072 2.706 3.84 6.635 10.83 18．（本小题满分 12 分）m 为何实数时，复数 z＝(2＋i)m2－3(i＋1)m－2(1－i)是： （1）实数；（2）虚数；（3）纯虚数？ 19．（本小题满分 12 分）某产品的广告费支出 x(单位:百万元)与销售额 y(单位:百万元之间 有如下数据: x 2 4 5 6 8 y 30 40 60 50 70 （1）画出散点图； （2）求 y 关于 x 的回归直线方程； （3）预测广告费为 9 百万元时的销售额是多少? 20．（本小题满分 12 分）设 是奇函数，其图象在点 处 的切线与直线 垂直，导函数 的最小值为 。 （1）求 的值； （2）求 在 上的最值。 21．（本小题满分 12 分）在平面直角坐标系中，以坐标原点为极点，x 轴的非负半轴为极轴 建立极坐标系。已知点 A 的极坐标为( 2， π 4 )，直线 m 的极坐标方程为 ρcos(θ－π 4 )＝ a，且点 A 在直线 m 上。 （1）求 a 的值及直线 m 的直角坐标方程； 2 2× 2 2 ( ) ( )( )( )( ) n ad bcK a b c d a c b d −= + + + + n a b c d= + + + ( ) ( )3 0f x ax bx c a= + + ≠ (1 (1))f， 6 7 0x y− − = ( )'f x 12− a b c、 、 ( )f x [ 13]− ， （2）圆的极坐标方程为 (α 为参数)，试判断直线 m 与圆的位置关系。 22．（本小题满分 12 分）已知函数 f（x）＝x3＋ax2＋bx＋c 在 x＝－ 与 x＝1 时都取得极值。 （1）求 a、b 的值与函数 f（x）的单调区间； （2）若对 ，不等式 恒成立，求 c 的取值范围。 αρ cos2= 2 3 ]2,1[−∈x 2)( cxf < 数学试卷（文科） 一、选择题：(本大题共 12 小题，每小题 分，满分 60 分，在每小题给出的四个选项中，只 有一项是符合题目要求的．) 题 号 1 2 3 4 5 6 7 8 9 10 11 12 答 案 D A C A A D B C C C C A 二.填空题： 13、 14、1 15、 16、 三、解答题：本大题共 6 小题，满分 70 分。解答须写出文字说明，证明过程或步骤。 17．(本题满分 10 分) 解：（1）2×2 列联表如下： 及格 不及格 合计 甲班 36 4 40 乙班 24 16 40 合计 60 20 80 18．（本小题满分 12 分） 解：z＝(2＋i)m2－3(i＋1)m－2(1－i) ＝2m2＋m2i－3mi－3m－2＋2i ＝(2m2－3m－2)＋(m2－3m＋2)i. (1)由 m2－3m＋2＝0 得 m＝1 或 m＝2， 即 m＝1 或 2 时，z 为实数． (2)由 m2－3m＋2≠0 得 m≠1 且 m≠2， 即 m≠1 且 m≠2 时，z 为虚数． (3)由Error!，得 m＝－ 1 2， 5 i )4,2 3( 291312111098765 =++++++++ 即 m＝－ 1 2时，z 为纯虚数． 19．(本小题满分 12 分) 解：（1）图略 （2）由散点图知,y 与 x 有线性相关，设回归方程为： （3） 答：略 20．(本小题满分 12 分) ˆy bx a= + 5 5 2 1 1 5 50 145 1380 = = = = = =∑ ∑i i i i i x y x x y    5 5 2 1 1 5 1 5 22 1 5 50 145 1380 5 6 5 17 5 5 6 5 17 5 i i i i i i i i i i x y x x y x y xy b . a y bx . x x y . x . = = = = = = = = − = = = − = − = + ∑ ∑ ∑ ∑  故 9 76= =x y当 时， （百万元） [ 21．(本题满分 12 分) 解析：(1)由点 A ( 2， π 4 )在直线 ρcos(θ－ π 4 )＝a 上，可得 a＝ 2. 所以直线 m 的方程可化为 ρcos θ＋ρsin θ＝2，从而直线 m 的直角坐标方程为 x＋y－ 2＝0. (2)由已知得圆 C 的直角坐标方程为 (x－1)2＋y2＝1. 所以圆心为(1，0)，半径 r＝1， 则圆心到直线 m 的距离 d＝ 2 2 <1，所以直线 m 与圆 C 相交． 22．(本小题满分 12 分) 解：⑴a＝ ，b＝－2 f（x）的递增区间是（－∞，－ ）与（1，＋∞） 递减区间是（－ ，1） ⑵c<－1 或 c>2 1 2 － 2 3 2 3