江苏省无锡市2021届新高考模拟化学试题(校模拟卷)含解析 21页

江苏省无锡市 2021 届新高考模拟化学试题（校模拟卷） 一、选择题：本题共 12 小题，每小题 5 分，共 60 分。在每小题给出的四个选项中，只有一项是符合题目 要求的。 1．已知函数 ( ) cos(2 ) 3 f x x ，则下列结论错误的是 ( ) A．函数 f x 的最小正周期为 π B．函数 f x 的图象关于点 ,0 12 对称 C．函数 f x 在 2, 3 3 上单调递增 D．函数 f x 的图象可由 sin 2y x 的图象向左平移 12 个单位长度得到 【答案】 D 【解析】 【分析】 由 2πT 可判断选项 A；当 π 12 x 时， π π2 = 3 2 x 可判断选项 B；利用整体换元法可判断选项 C； πsin 2 12 y x πcos 2 3 x f x 可判断选项 D. 【详解】 由题知 πcos 2 3 f x x ，最小正周期 2π π 2 T ，所以 A 正确；当 π 12 x 时， π π2 = 3 2 x ，所以 B 正确；当 π 2π, 3 3 x 时， π 5π2 π, 3 3 x ，所以 C 正确；由 sin 2y x 的图象向左平移 π 12 个单位，得 π π π πsin 2 sin 2 sin 2 12 6 2 3 y x x x πcos 2 3 x f x ，所以 D 错误 . 故选： D. 【点睛】 本题考查余弦型函数的性质，涉及到周期性、对称性、单调性以及图象变换后的解析式等知识，是一道中 档题 . 2．设不等式组 2 0 0 0 x x y x y ，表示的平面区域为 Ω，在区域 Ω内任取一点 ,P x y ，则 P 点的坐标满 足不等式 2 2 2x y 的概率为 A． π 8 B． π 4 C． 1 2 π D． 1 2 π 【答案】 A 【解析】 【分析】 画出不等式组表示的区域 Ω，求出其面积， 再得到 2 2 2x y 在区域 Ω内的面积， 根据几何概型的公式， 得到答案 . 【详解】 画出 2 0 0 0 x x y x y 所表示的区域 Ω，易知 2,2 , 2, 2A B ， 所以 AOB 的面积为 4， 满足不等式 2 2 2x y 的点，在区域 Ω内是一个以原点为圆心， 2 为半径的 1 4 圆面，其面积为 2 ， 由几何概型的公式可得其概率为 2= = 4 8 P ， 故选 A 项 . 【点睛】 本题考查由约束条件画可行域，求几何概型，属于简单题 . 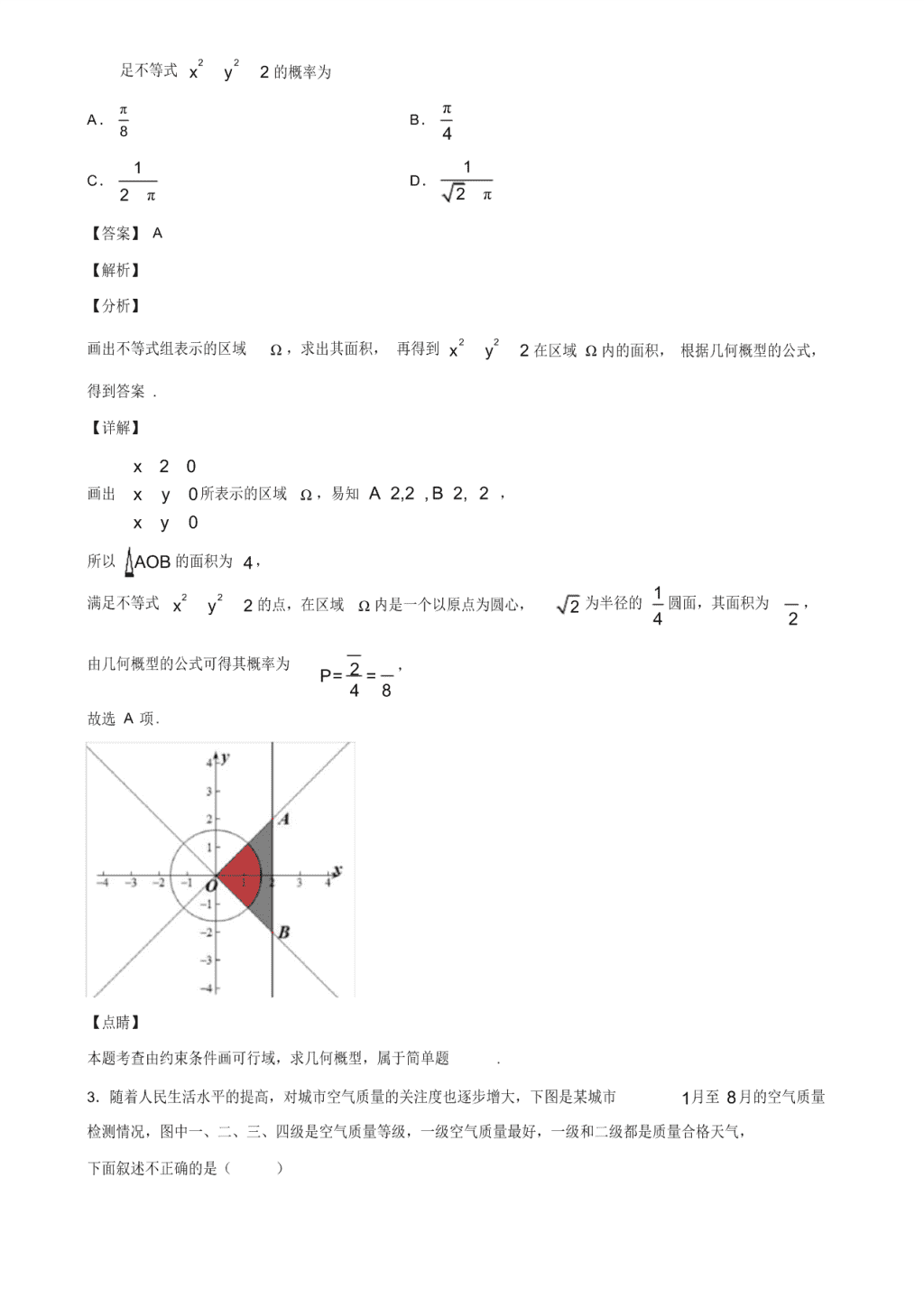3．随着人民生活水平的提高，对城市空气质量的关注度也逐步增大，下图是某城市 1月至 8月的空气质量 检测情况，图中一、二、三、四级是空气质量等级，一级空气质量最好，一级和二级都是质量合格天气， 下面叙述不正确的是（ ） A． 1 月至 8 月空气合格天数超过 20天的月份有 5 个 B．第二季度与第一季度相比，空气达标天数的比重下降了 C． 8 月是空气质量最好的一个月 D． 6 月份的空气质量最差 . 【答案】 D 【解析】 由图表可知 5月空气质量合格天气只有 13天， 5 月份的空气质量最差．故本题答案选 D ． 4．已知 (1 ) 2i ai bi （i 为虚数单位， ,a b R ），则 ab 等于（ ） A． 2 B．-2 C． 1 2 D． 1 2 【答案】 A 【解析】 【分析】 利用复数代数形式的乘除运算化简，再由复数相等的条件列式求解． 【详解】 (1 ) 2i ai bi ， 2a i bi ，得 2a ， 1b ． 2ab ． 故选： A ． 【点睛】 本题考查复数代数形式的乘除运算，考查复数相等的条件，意在考查学生对这些知识的理解掌握水平，是 基础题． 5．函数 2sin cos( ) 20 x x xf x x 在 [ 2 ,0) (0,2 ] 上的图象大致为 ( ) A． B． C． D． 【答案】 A 【解析】 【分析】 首先判断函数的奇偶性，再根据特殊值即可利用排除法解得； 【详解】 解：依题意， 2 2sin( ) ( ) cos( ) sin cos( ) ( ) 20 20 x x x x x xf x f x x x ，故函数 f x 为偶函数，图 象关于 y 轴对称，排除 C； 而 2 ( ) 0 20 f ，排除 B； 2 (2 ) 0 5 f ，排除 D. 故选： A . 【点睛】 本题考查函数图象的识别，函数的奇偶性的应用，属于基础题 . 6．定义在 2 2, 上的函数 f x 与其导函数 f x 的图象如图所示，设 O 为坐标原点， A 、 B 、 C 、 D 四点的横坐标依次为 1 2 、 1 6 、1、 4 3 ，则函数 x f xy e 的单调递减区间是（ ） A． 1 4, 6 3 B． 1 ,1 2 C． 1 1, 2 6 D． 1,2 【答案】 B 【解析】 【分析】 先辨别出图象中实线部分为函数 y f x 的图象，虚线部分为其导函数的图象，求出函数 x f x y e 的 导数为 x f x f x y e ，由 0y ，得出 f x f x ，只需在图中找出满足不等式 f x f x 对 应的 x 的取值范围即可 . 【详解】 若虚线部分为函数 y f x 的图象，则该函数只有一个极值点，但其导函数图象（实线）与 x 轴有三个 交点，不合乎题意； 若实线部分为函数 y f x 的图象，则该函数有两个极值点，则其导函数图象（虚线）与 x 轴恰好也只 有两个交点，合乎题意 . 对函数 x f x y e 求导得 x f x f x y e ，由 0y 得 f x f x ， 由图象可知，满足不等式 f x f x 的 x 的取值范围是 1 ,1 2 ， 因此，函数 x f x y e 的单调递减区间为 1 ,1 2 . 故选： B. 【点睛】 本题考查利用图象求函数的单调区间， 同时也考查了利用图象辨别函数与其导函数的图象， 考查推理能力， 属于中等题 . 7．已知 ,m n 表示两条不同的直线， ， 表示两个不同的平面， 且 ,m n ，则 “ ”是 “ //m n ” 的 ( )条件 . A．充分不必要 B．必要不充分 C．充要 D．既不充分也不必要 【答案】 B 【解析】 【分析】 根据充分必要条件的概念进行判断 . 【详解】 对于充分性：若 ，则 ,m n 可以平行，相交，异面，故充分性不成立； 若 //m n ，则 ,n n ，可得 ，必要性成立 . 故选： B 【点睛】 本题主要考查空间中线线， 线面， 面面的位置关系， 以及充要条件的判断， 考查学生综合运用知识的能力 . 解决充要条件判断问题，关键是要弄清楚谁是条件，谁是结论 . 8．已知 O 为坐标原点，角 的终边经过点 (3, )( 0)P m m 且 10sin 10 m ，则 sin 2 ( ) A． 4 5 B． 3 5 C． 3 5 D． 4 5 【答案】 C 【解析】 【分析】 根据三角函数的定义，即可求出 1m ，得出 (3, 1)P ，得出 sin 和 cos ，再利用二倍角的正弦公式， 即可求出结果 . 【详解】 根据题意， 2 10sin 109 m m m ，解得 1m ， 所以 (3, 1)OP ， 所以 10 3 10sin ,cos 10 10 ， 所以 3sin 2 2sin cos 5 . 故选： C. 【点睛】 本题考查三角函数定义的应用和二倍角的正弦公式，考查计算能力 . 9．若复数 z 满足 1 i z i （ i 是虚数单位） ，则 z 的虚部为（ ） A． 1 2 B． 1 2 C． 1 2 i D． 1 2 i 【答案】 A 【解析】 【分析】 由 1 i z i 得 1 z i i ,然后分子分母同时乘以分母的共轭复数可得复数 z ,从而可得 z 的虚部 . 【详解】 因为 (1 )i z i , 所以 2 2 (1 ) 1 1 1 1 (1 )(1 ) 1 1 2 21 i i i i i iz i i i i i , 所以复数 z 的虚部为 1 2 . 故选 A. 【点睛】 本题考查了复数的除法运算和复数的概念 ,属于基础题 .复数除法运算的方法是分子分母同时乘以分母的共 轭复数 ,转化为乘法运算 . 10．已知七人排成一排拍照，其中甲、乙、丙三人两两不相邻，甲、丁两人必须相邻，则满足要求的排队 方法数为（ ）. A． 432 B．576 C．696 D． 960 【答案】 B 【解析】 【分析】 先把没有要求的 3 人排好，再分如下两种情况讨论： 1.甲、丁两者一起，与乙、丙都不相邻， 2.甲、丁一 起与乙、丙二者之一相邻 . 【详解】 首先将除甲、乙、丙、丁外的其余 3 人排好，共有 3 3A 种不同排列方式，甲、丁排在一起共有 2 2A 种不同方 式； 若甲、丁一起与乙、丙都不相邻，插入余下三人产生的空档中，共有 3 4A 种不同方式； 若甲、丁一起与乙、丙二者之一相邻，插入余下三人产生的空档中，共有 1 2 2 4C A 种不同方式； 根据分类加法、分步乘法原理，得满足要求的排队方法数为 3 3A 2 2A 3 4( A 1 2 2 4 ) 576C A 种 . 故选： B. 【点睛】 本题考查排列组合的综合应用，在分类时，要注意不重不漏的原则，本题是一道中档题 . 11．已知平面向量 ,a b 满足 | | | |a b ，且 ( 2 )a b b ，则 ,a b 所夹的锐角为（ ） A． 6 B． 4 C． 3 D． 0 【答案】 B 【解析】 【分析】 根据题意可得 ( 2 ) 0a b b ，利用向量的数量积即可求解夹角 . 【详解】 因为 ( 2 ) ( 2 ) 0a b b a b b 即 22 | |a b b 而 2 2cos , 2| | | | | | a b a ba b a b b 所以 ,a b 夹角为 4 故选： B 【点睛】 本题考查了向量数量积求夹角，需掌握向量数量积的定义求法，属于基础题 . 12．已知某几何体的三视图如图所示， 其中正视图与侧视图是全等的直角三角形， 则该几何体的各个面中， 最大面的面积为（ ） A． 2 B．5 C． 13 D． 22 【答案】 D 【解析】 【分析】 根据三视图还原出几何体，找到最大面，再求面积 . 【详解】 由三视图可知，该几何体是一个三棱锥，如图所示，将其放在一个长方体中，并记为三棱锥 P ABC . 13PAC PABS S ， 22PACS ， 2ABCS ，故最大面的面积为 22 .选 D. 【点睛】 本题主要考查三视图的识别，复杂的三视图还原为几何体时，一般借助长方体来实现 . 二、填空题：本题共 4 小题，每小题 5 分，共 20 分。 13．某班有学生 52 人,现将所有学生随机编号 ,用系统抽样方法 ,抽取一个容量为 4 的样本 ,已知 5 号、 31 号、 44 号学生在样本中 ,则样本中还有一个学生的编号是 __________． 【答案】 18 【解析】 【分析】 根据系统抽样的定义和方法 ,所抽取的 4 个个体的编号成等差数列 ,故可根据其中三个个体的编号求出另一 个个体的编号 . 【详解】 解：根据系统抽样的定义和方法 ,所抽取的 4 个个体的编号成等差数列 , 已知其中三个个体的编号为 5,31,44, 故还有一个抽取的个体的编号为 18, 故答案为 :18 【点睛】 本题主要考查系统抽样的定义和方法 ,属于简单题 . 14．设 x R ，则 “ 3 8x ”是 “ 2x ”的__________条件 . 【答案】充分必要 【解析】 【分析】 根据充分条件和必要条件的定义可判断两者之间的条件关系 . 【详解】 当 3 8x 时，有 2x ，故 “ 3 8x ”是 “ 2x ”的充分条件 . 当 2x 时，有 3 8x ，故 “ 3 8x ”是 “ 2x ”的必要条件 . 故 “ 3 8x ”是 “ 2x ”的充分必要条件， 故答案为：充分必要 . 【点睛】 本题考查充分必要条件的判断， 可利用定义来判断， 也可以根据两个条件构成命题及逆命题的真假来判断， 还可以利用两个条件对应的集合的包含关系来判断，本题属于容易题 . 15．设集合 1 A a， ， ee 2 a B ， （其中 e 是自然对数的底数） ，且 A B ，则满足条件的实数 a 的个数为 ______． 【答案】 1 【解析】 【分析】 可看出 2 a a e ，这样根据 A B 即可得出 2a ，从而得出满足条件的实数 a 的个数为 1． 【详解】 解： A B ， 2a 或 2 a a e ， 在同一平面直角坐标系中画出函数 y x 与 2 x y e 的图象， 由图可知 y x 与 2 x y e 无交点， 2 a a e 无解，则满足条件的实数 a 的个数为 1． 故答案为： 1． 【点睛】 考查列举法的定义，交集的定义及运算，以及知道方程 2 x x e 无解，属于基础题． 16．有编号分别为 1，2， 3，4，5 的 5 个红球和 5 个黑球，从中随机取出 4 个，则取出球的编号互不相同 的概率为 _______________. 【答案】 8 21 【解析】 试题分析：从编号分别为 1，1，3，4，5 的 5 个红球和 5 个黑球，从中随机取出 4 个，有 4 10 210C 种不 同的结果，由于是随机取出的，所以每个结果出现的可能性是相等的；设事件 A 为“取出球的编号互不相 同 ”， 则事件 A 包含了 1 1 1 1 1 5 2 2 2 2 80C C C C C 个基本事件，所以 80 8 210 21 P A . 考点： 1.计数原理； 1．古典概型 . 三、解答题：共 70 分。解答应写出文字说明、证明过程或演算步骤。 17．已知椭圆 C： 2 2 2 2+ =1x y a b （a＞b＞0）过点（ 0, 2 ），且满足 a+b＝ 3 2 ． （ 1）求椭圆 C 的方程； （ 2）若斜率为 1 2 的直线与椭圆 C 交于两个不同点 A，B，点 M 坐标为（ 2,1），设直线 MA 与 MB 的斜率 分别为 k 1， k2，试问 k 1+k 2 是否为定值？并说明理由． 【答案】 （1） 2 2 + =1 8 2 x y （ 2）k 1+k 2 为定值 0，见解析 【解析】 【分析】 （ 1）利用已知条件直接求解 ,a b ，得到椭圆的方程； （ 2）设直线在 y 轴上的截距为 m ，推出直线方程，然后将直线与椭圆联立，设 1 1 2 2, ,A B xyx y， ， 利用韦达定理求出 1 2k k ，然后化简求解即可 . 【详解】 （ 1）由椭圆过点（ 0, 2 ），则 2b ，又 a+b ＝3 2 ，所以 2 2a ， 故椭圆的方程为 2 2 + =1 8 2 x y ； （ 2） 1 2 0k k ，证明如下： 设直线在 y 轴上的截距为 m ，所以直线的方程为： 1 2 y x m ， 由 2 2 1 2 + =1 8 2 y x m x y 得： 2 22 2 4 0x mx m ， 由 2 24 8 16 0m m 得 2 2m ， 设 1 1 2 2, ,A B xyx y， ，则 2 1 2 1 22 2 4，x x m x x m ， 所以 1 2 2 11 2 1 2 1 2 1 2 1 2 1 21 1 2 2 2 2 = y x y xy yk k x x x x ， 又 1 1 2 2 1 1 2 2 ，y x m y x m ， 所以 1 2 2 1 1 2 1 21 2 1 2 2 4 1=y x y x x x m x x m 22 4 2 2 4 1 0m m m m ， 故 1 2 0k k . 【点睛】 本题主要考查了椭圆的标准方程的求解，直线与椭圆的位置关系的综合应用，考查了方程的思想，转化与 化归的思想，考查了学生的运算求解能力 . 18．如图 ,三棱柱 1 1 1ABC A B C 中 ,底面 ABC 是等边三角形 ,侧面 1 1BCC B 是矩形 , 1 ,AB A B N 是 1B C 的中 点 ,M 是棱 1AA 上的点 ,且 1AA CM . （ 1）证明： / /MN 平面 ABC ； （ 2）若 1AB A B ,求二面角 A CM N 的余弦值 . 【答案】 （1）见解析（ 2） 2 5 5 【解析】 【分析】 （ 1）连结 BM ，推导出 BC⊥ BB 1，AA 1⊥BC，从而 AA 1⊥MC ，进而 AA 1⊥平面 BCM ，AA 1⊥MB ，推 导出四边形 AMNP 是平行四边形，从而 MN ∥AP ，由此能证明 MN ∥平面 ABC ． （ 2）推导出 △ABA 1是等腰直角三角形，设 AB 2a ，则 AA 1＝2a，BM ＝AM ＝a，推导出 MC ⊥BM ， MC ⊥AA 1，BM ⊥AA 1，以 M 为坐标原点， MA 1，MB ，MC 为 x， y，z 轴，建立空间直角坐标系，利用 向量法能求出二面角 A﹣CM ﹣N 的余弦值． 【详解】 （ 1）如图 1，在三棱柱 1 1 1ABC A B C 中，连结 BM ，因为 1 1BCC B 是矩形， 所以 1BC BB ，因为 1 1/ /AA BB ，所以 1AA BC ， 又因为 1AA MC ， BC MC C ，所以 1AA 平面 BCM ， 所以 1AA MB ，又因为 1AB A B ，所以 M 是 1AA 中点， 取 BC 中点 P ，连结 NP ， AP ，因为 N 是 1B C 的中点，则 1/ /NP BB 且 1 1 2 NP BB ， 所以 / /NP MA 且 NP MA ，所以四边形 AMNP 是平行四边形，所以 / /MN AP， 又因为 MN 平面 ABC ， AP 平面 ABC ，所以 / /MN 平面 ABC . （图 1） （图 2） （ 2）因为 1AB A B ，所以 1ABA 是等腰直角三角形，设 2AB a ， 则 1 2AA a ， BM AM a .在 Rt ACM 中， 2AC a ，所以 MC a . 在 BCM 中， 2 2 2 22CM BM a BC ，所以 MC BM ， 由（ 1）知，则 1MC AA ， 1BM AA ，如图 2，以 M 为坐标原点， 1MA ， MB ， MC 的方向分别为 x 轴， y 轴， z 轴的正方向建立空间直角坐标系， 则 0,0,0M ， 0,0,C a ， 1 2 , ,0B a a . 所以 , , 2 2 a aN a ，则 0,0,MC a ， , , 2 2 a aMN a ， 设平面 CMN 的法向量为 1 , ,n x y z ， 则 1 1 0, 0, n MC n MN 即 0, 0. 2 2 az a aax y z 取 1x 得 2y .故平面 CMN 的一个法向量为 1 1, 2,0n ， 因为平面 ACM 的一个法向量为 2 0,1,0n ， 则 1 2 1 2 1 2 2 5cos , 5 n nn n n n . 因为二面角 A CM N 为钝角， 所以二面角 A CM N 的余弦值为 2 5 5 . 【点睛】 本题考查线面平行的证明，考查了利用空间向量法求解二面角的方法，考查空间中线线、线面、面面间的 位置关系等基础知识，考查运算求解能力，是中档题． 19．已知函数 ( ) ln( ) ,( 0)f x ax a a ． （ 1）若函数 ( ) ( )xh x e f x 在 (0, ) 上单调递增，求实数 a 的值； （ 2）定义： 若直线 :l y kx b 与曲线 1 1 2 2: ( , ) 0 ( , ) 0:C f x y C f x y、 都相切， 我们称直线 l 为曲线 1C 、 2C 的公切线，证明：曲线 ( ) ln( ) ,( 0)f x ax a a 与 ( ) ,( 0)xg x ae a 总存在公切线． 【答案】 （1） 1a ；（2）见解析 . 【解析】 【分析】 （ 1）求出导数，问题转化为 ( ) 0h x 在 (0, ) 上恒成立，利用导数求出 1( ) ln( )x ax a x 的最小值 即可求解； （ 2）分别设切点横坐标为 1 2,x x ，利用导数的几何意义写出切线方程，问题转化为证明两直线重合，只需 满足 2 2 2 1 1 2 1 ln( ) 1 x x x ae x ax a ae ax e 有解即可，利用函数的导数及零点存在性定理即可证明存在 . 【详解】 （ 1） ( ) [ln( ) ], 0xh x e ax a x ， 1( ) ln ) ]([xh x e ax a x 函数 ( )h x 在 (0, ) 上单调递增等价于 ( ) 0h x 在 (0, ) 上恒成立． 令 1( ) ln( )x ax a x ，得 2 2 1 1 1( ) xx x x x ， 所以 ( )x 在 (0,1) 单调递减，在 (1, ) 单调递增，则 min( ) (1)x ． 因为 0xe ，则 ( ) 0h x 在 (0, ) 上恒成立等价于 ( ) 0x 在 (0, ) 上恒成立； 又 1( ) 0, a 1( ) (1) 0 a ， 所以 1 1 a ，即 1a ． （ 2）设 ( ) ln( ) ,( 0)f x ax a a 的切点横坐标为 1x x ，则 1 1 ( ) 1f x x 切线方程为 1 1 1 1ln( ) ( )y ax a x x x ⋯⋯ ① 设 ( ) ,( 0)xg x ae a 的切点横坐标为 2x x ，则 2 2( ) xg x ae ， 切线方程为 2 2 2( )x xy ae ae x x ⋯⋯ ② 若存在 1 2,x x ，使①②成为同一条直线，则曲线 ( )f x 与 ( )g x 存在公切线，由①②得 2 2 2 1 1 2 1 ln( ) 1 x x x ae x ax a ae ax e 消去 1x 得 2 2 2 21 x xx a ae ax e 即 2 2 22 2 2 1 11 2 1 1 1 ( )x x xe x ee a x x 令 2 1( ) 1 x x et x e x ，则 2 2 1( ) 0 ( 1) x xx e et x x 所以，函数 ( )y t x 在区间 (0, ) 上单调递增， 0(1) (2) 0 (1,2)t t x ，使得 0( ) 0t x 0( , )x x 时总有 0( ) ( ) 0t x t x 又 x 时， ( )t x 1 ( 1) 1 1 xe x a x 在 (0, ) 上总有解 综上，函数 ( ) ln( ) ,( 0)f x ax a a 与 ( ) ,( 0)xg x ae a 总存在公切线． 【点睛】 本题主要考查了利用导数研究函数的恒成立问题，导数的几何意义，利用导数证明方程有解，属于难题 . 20．己知点 E ， F 分别是椭圆 2 2 2 2: 1 0x yC a b a b 的上顶点和左焦点，若 EF 与圆 2 2 4 3 x y 相 切于点 T ，且点 T 是线段 EF 靠近点 E 的三等分点 . 1 求椭圆 C 的标准方程； 2 直线 :l y kx m 与椭圆 C 只有一个公共点 P ，且点 P 在第二象限，过坐标原点 O 且与 l 垂直的直线 l 与圆 2 2 8x y 相交于 A， B 两点，求 PAB△ 面积的取值范围 . 【答案】 1 2 2 1 6 2 x y ; 2 0, 4 3 4 . 【解析】 【分析】 1 连接 OT ，由三角形相似得， 2 4 3 OT ET TF ，进而得出 2 6a ， 2 2 2 2 2b OE OT ET ， 写出椭圆 C 的标准方程； 2 由 2 2 1 6 2 y kx m x y 得， 2 2 23 1 6 3 6 0k x kmx m ，因为直线 :l y kx m 与椭圆 C 相切于点 P ， 0，解得 2 3 3 1 kmx k ， 23 1 my k ，因为点 P 在第二象限， 所以 0k ， 0m ，所以 26 2m k ， 设直线 l 与 l 垂直交于点 Q ，则 PQ 是点 P 到直线 l 的距离，设直线 l 的方程为 1y x k ，则 6 2PQ ，求出 PAB△ 面积的取值范围 . 【详解】 解： 1 连接 OT ，由 EOT OFT∽ 可得 2 1 2 4 3 3 3 OT ET TF a a ， 2 6a ， 2 2 2 2 2b OE OT ET ， 椭圆 C 的标准方程 2 2 1 6 2 x y ； 2 由 2 2 1 6 2 y kx m x y 得， 2 2 23 1 6 3 6 0k x kmx m ， 因为直线 :l y kx m 与椭圆 C 相切于点 P ， 所以 2 2 2 2 2 6 4 3 1 3 6 12 6 2 0km k m k m ，即 2 26 2m k ， 解得 2 3 3 1 kmx k ， 23 1 my k ， 即点 P 的坐标为 2 2 3 , 3 1 3 1 km m k k ， 因为点 P 在第二象限，所以 0k ， 0m ， 所以 26 2m k ， 所以点 P 的坐标为 2 2 3 2 2, 3 1 3 1 k k k ， 设直线 l 与 l 垂直交于点 Q ，则 PQ 是点 P 到直线 l 的距离， 设直线 l 的方程为 1y x k ， 则 2 2 2 1 3 2 2 3 1 3 1 1 1 k k k kPQ k 4 2 2 2 2 2 2 2 2 2 13 4 1 4 2 33 4 k k k k k 2 2 6 2 3 1 ， 当且仅当 2 2 13k k ，即 2 3 3 k 时， PQ 有最大值 6 2 ， 所以 1 4 2 4 3 4 2PABS PQ ，即 PAB△ 面积的取值范围为 0, 4 3 4 . 【点睛】 本题考查直线和椭圆位置关系的应用，利用基本不等式，属于难题 . 21．为迎接 2022 年冬奥会，北京市组织中学生开展冰雪运动的培训活动，并在培训结束后对学生进行了 考核．记 X 表示学生的考核成绩，并规定 85X 为考核优秀．为了了解本次培训活动的效果，在参加培 训的学生中随机抽取了 30 名学生的考核成绩，并作成如下茎叶图： （Ⅰ）从参加培训的学生中随机选取 1 人，请根据图中数据，估计这名学生考核优秀的概率； （Ⅱ）从图中考核成绩满足 80,89X 的学生中任取 2 人，求至少有一人考核优秀的概率； （Ⅲ）记 ( )P a X b 表示学生的考核成绩在区间 ,a b 的概率，根据以往培训数据，规定当 85 1 0.5 10 xP 时培训有效．请根据图中数据，判断此次中学生冰雪培训活动是否有效，并说明理 由． 【答案】 （Ⅰ） 7 30 （Ⅱ） 3 5 （Ⅲ）见解析 【解析】 【分析】 （Ⅰ）根据茎叶图求出满足条件的概率即可； （Ⅱ）结合图表得到 6 人中有 2 个人考核为优，从而求出满足条件的概率即可； （Ⅲ）求出满足 85 1 10 X 的成绩有 16 个，求出满足条件的概率即可． 【详解】 解：（Ⅰ）设这名学生考核优秀为事件 A， 由茎叶图中的数据可以知道， 30 名同学中，有 7 名同学考核优秀， 所以所求概率 P A 约为 7 30 （Ⅱ）设从图中考核成绩满足 80,89X 的学生中任取 2 人， 至少有一人考核成绩优秀为事件 B ， 因为表中成绩在 80,89 的 6 人中有 2 个人考核为优， 所以基本事件空间 包含 15 个基本事件，事件 B 包含 9 个基本事件， 所以 9 3( ) 15 5 P B （Ⅲ）根据表格中的数据，满足 85 1 10 x 的成绩有 16 个， 所以 85 16 81 0.5 10 30 15 xP 所以可以认为此次冰雪培训活动有效． 【点睛】 本题考查了茎叶图问题，考查概率求值以及转化思想，是一道常规题． 22．在直角坐标系 xOy 中， 椭圆 2 2 2 2: 1( 0)x yC a b a b 的左、 右焦点分别为 1 2,F F ，点 M 在椭圆 C 上 且 2MF x 轴，直线 1MF 交 y 轴于 H 点， 2 4 OH ，椭圆 C 的离心率为 2 2 . （ 1）求椭圆 C 的方程； （ 2）过 1F 的直线 l 交椭圆 C 于 ,A B 两点，且满足 2OA OB BA OB ，求 ABO 的面积 . 【答案】 （1） 2 2 1 2 x y ；（2） 2 3 5 . 【解析】 【分析】 （ 1）根据离心率以及 2 2MF OH ，即可列方程求得 , ,a b c ，则问题得解； （ 2）设直线方程为 1x my ，联立椭圆方程，结合韦达定理，根据题意中转化出的 0OA OB ，即可 求得参数 m ，则三角形面积得解 . 【详解】 （ 1）设 2( ,0)F c ，由题意可得 2 2 2 2 2 1, M x y by a b a . 因为 OH 是 1 2F F M 的中位线，且 2 4 OH ， 所以 2 2| | 2 MF ，即 2 2 2 b a ， 因为 2 2 22 , 2 ce a b c a 进而得 2 21, 2b a ， 所以椭圆方程为 2 2 1 2 x y （ 2）由已知得 2 2OA OB OA OB 两边平方 整理可得 0OA OB . 当直线 l 斜率为 0时，显然不成立 . 直线 l 斜率不为 0时， 设直线 l 的方程为 1 1 2 21. ( , ). ( , )x my A x y B x y ， 联立 2 2 1 1 2 x my x y 消去 x ，得 2 2( 2) 2 1 0m y my ， 所以 1 2 1 22 2 2 1, 2 2 my y y y m m ， 由 0OA OB 得 1 2 1 2 0x x y y 将 1 1 2 21, 1x my x my 代入 整理得 1 2 1 2( 1)( 1) 0my my y y ， 展开得 2 1 2 1 2 1 2( ) 1 0m y y m y y y y ， 整理得 2 2 m ， 所以 1 1 2 1 2 3 2 5ABOS OF y y .即为所求 . 【点睛】 本题考查由离心率求椭圆的方程，以及椭圆三角形面积的求解，属综合中档题 . 23．本小题满分 14 分） 已知曲线 C 的极坐标方程为 4sin ，以极点为原点， 极轴为 x 轴的非负半轴建立平面直角坐标系， 直线 l 的参数方程为 1 , 2 3 1 2 x t y t （ t 为参数），求直线 l 被曲线 C 截得的线段的长度 【答案】 15) 2 1(22 22 【解析】解：解：将曲线 C 的极坐标方程化为直角坐标方程为 2 2 4 0x y y ， 即 2 2( 2) 4x y ，它表示以 (0, 2) 为圆心， 2 为半径圆， ⋯⋯⋯⋯⋯⋯⋯⋯⋯4 分 直线方程 l 的普通方程为 3 1y x ， ⋯⋯⋯8 分 圆 C 的圆心到直线 l 的距离 2 1d ，⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯ 10分 故直线 l 被曲线 C 截得的线段长度为 15) 2 1(22 22 ．⋯⋯⋯⋯⋯ 14分