山东省滕州市第一中学2019-2020学年高一5月摸底考试数学试题 11页

高一摸底考试数学试题 一、单选题 ‎1．分层随机抽样又称类型抽样，即将相似的个体归入一类（层），然后每类抽取若干个个体构成样本，所以分层随机抽样为保证每个个体等可能抽样，必须进行（ ）‎ A．每层等可能抽样 B．每层可以不等可能抽样 C．所有层按同一抽样比等可能抽样 D．所有层抽取的个体数量相同 ‎2．是虚数单位，复数满足，则 A．或 B．或 C． D．‎ ‎3．设，向量，，，且，，则 ＝（ ）‎ A． B． C． D．10‎ ‎4．如图，是水平放置的的直观图，，，则的面积是（ ）‎ A． B． C． D．‎ ‎5．某学校位同学组成的志愿者组织分别由李老师和张老师负责，每次献爱心活动均需该组织位同学参加.假设李老师和张老师分别将各自活动通知的信息独立，随机地发给位同学，且所发信息都能收到.则甲同学收到李老师或张老师所发活动通知的信息的概率为（ ）‎ A． B． C． D．‎ ‎6．在中，角，，所对的边分别为，，，，则的形状一定是（ ）‎ A．直角三角形 B．锐角三角形 C．等腰三角形 D．等腰直角三角形 ‎7．在‎△ABC中，向量AB与AC满足ABAB‎+‎ACAC‎·BC=0‎，且BABA‎·BCBC=‎‎2‎‎2‎，则‎△ABC为‎(‎   ‎‎)‎ A. 等边三角形 B. 直角三角形 C. 等腰非等边三角形 D. 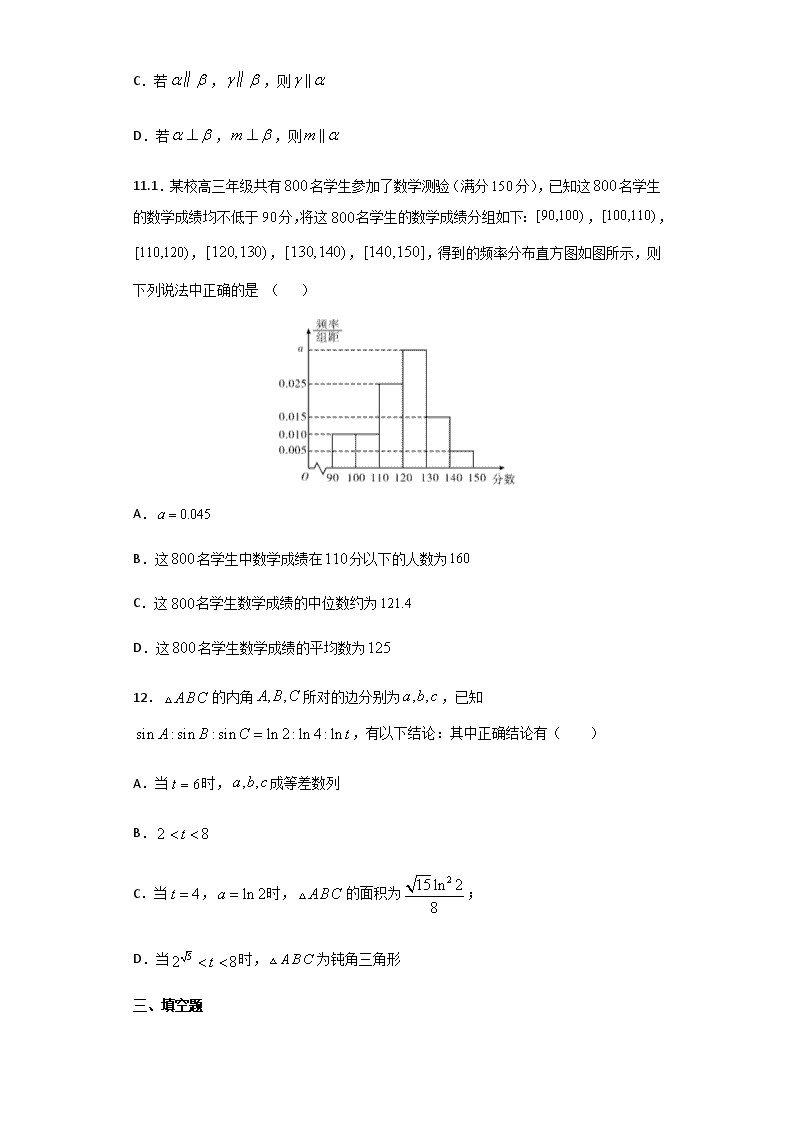等腰直角三角形 ‎8．如图，在棱长为的正方体中，点、分别是棱，的中点，是侧面内一点，若平面，则线段长度的取值范围是（ ）‎ A． ‎ B． C． D．‎ 二、多选题 ‎9．已知,满足,则实数k的值可能为( )‎ A． B． C．58 D．‎ ‎10．已知是不重合的直线，是不重合的平面，则下列命题为假命题的是（ ）‎ A．若，，则 B．若，，，，则 C．若，，则 D．若，，则 ‎11.1．某校高三年级共有名学生参加了数学测验（满分分），已知这名学生的数学成绩均不低于分，将这名学生的数学成绩分组如下：，，，，，，得到的频率分布直方图如图所示，则下列说法中正确的是 （ ）‎ A．‎ B．这名学生中数学成绩在分以下的人数为 C．这名学生数学成绩的中位数约为 D．这名学生数学成绩的平均数为 ‎12．的内角所对的边分别为，已知，有以下结论：其中正确结论有（ ）‎ A．当时，成等差数列 B．‎ C．当，时，的面积为；‎ D．当时，为钝角三角形 三、填空题 ‎13．设,则方程的解为_________.‎ ‎14.设的内角，，的对边分别为，，，若，且，则的面积为______.‎ ‎15．如图，一栋建筑物AB高（30-10）m，在该建筑物的正东方向有一个通信塔CD．在它们之间的地面M点（B、M、D三点共线）测得对楼顶A、塔顶C的仰角分别是15°和60°，在楼顶A处测得对塔顶C的仰角为30°，则通信塔CD的高为______m．‎ ‎16．已知平面向量，，，，且，若为平面单位向量，则的最小值为__________.‎ 四、解答题 ‎17．设是虚数,是实数,且.‎ ‎（1）求的值及的实部的取值范围;‎ ‎（2）设,求证为纯虚数.‎ ‎18.已知，的夹角为45°.‎ ‎（1）求的值;‎ ‎（2）若向量的夹角是锐角，求实数的取值范围.‎ ‎19.如图，四棱锥中，平面，，，，，分别为，的中点.‎ ‎（1）求证：平面平面；‎ ‎（2）若，求点到平面的距离.‎ ‎20.‎ 某校高三年级50名学生参加数学竞赛，根据他们的成绩绘制了如图所示的频率分布直方图，已知分数在的矩形面积为，‎ 求：分数在的学生人数；‎ 这50名学生成绩的中位数精确到；‎ 若分数高于60分就能进入复赛，从不能进入复赛的学生中随机抽取两名，求两人来自不同组的概率．‎ ‎21.已知在ΔABC中，角A,B,C的对边分别为a,b,c,且 ‎ ‎（1）求b的值；‎ ‎（2）若cosB+‎3‎sinB=2‎,求a+c的取值范围.‎ ‎22.如图所示，正四棱锥中，为底面正方形的中心，侧棱与底面所成的角的正切值为．‎ ‎（1）求侧面与底面所成的二面角的大小；‎ ‎（2）若是的中点，求异面直线与所成角的正切值；‎ ‎（3）问在棱上是否存在一点，使⊥侧面，若存在，试确定点的位置；若不存在，说明理由．‎ ‎ 高一摸底考试数学答案 ‎1．C 2．C 3．B 4．C 5．C 6．A 7.D 8.C ‎9.AB 10.ABD 11．BC 12．BD 13. ‎ 14． 15．60 16．‎ ‎17.解：（1）由是虚数,设 则,‎ 且,即,‎ 此时,,.即的实部的取值范围为.‎ ‎（2）设,‎ 又, 故是纯虚数.‎ ‎18.（1）∵‎ ‎∴‎ ‎（2）∵与的夹角是锐角 ‎∴，且与不能同向共线 ‎∴，，‎ ‎∴或 19. ‎（2）到平面的距离.‎ ‎20.（1）3人； （2）76.7； （3）.‎ ‎21.（1）由cosBb‎+cosCc=‎‎2‎3‎sinA‎3sinC，应用余弦定理，可得a‎2‎‎+c‎2‎-‎b‎2‎‎2abc‎+a‎2‎‎+b‎2‎-‎c‎2‎‎2abc=‎‎2‎3‎a‎3c ‎ 化简得‎2b=‎‎3‎则b=‎‎3‎‎2‎ ‎ ‎（2）‎∵‎ cosB+‎3‎sinB=2‎ ‎∴‎1‎‎2‎cosB+‎3‎‎2‎sinB=1‎即sin(π‎6‎+B)=1‎ ‎ ‎∵B∈(0,π)‎‎ ‎∴B+π‎6‎=‎π‎2‎ 所以B=‎π‎3‎ ‎ 法一.‎∵‎ ‎2R=bsinB=1‎,则a+c=sinA+sinC =sinA+sin(‎2π‎3‎-A)‎=‎3‎‎2‎sinA+‎3‎‎2‎cosA =‎3‎sin(A+π‎6‎)‎ ‎ 又‎∵0b=‎‎3‎‎2‎ 综上a+c∈(‎3‎‎2‎,‎3‎]‎ ‎22.（1）取中点，设面，连，‎ 则为二面角的平面角，‎ 为侧棱与底面所成的角，，‎ 设，，， ∴．‎ ‎（2）连，为异面直线与所成的角．‎ 因为，，所以平面.‎ 平面，所以.‎ ‎∵,∴。‎ ‎（3）延长交于，取中点，连、．‎ 因为，，，故平面，因平面，‎ 故平面平面， 又，故为等边三角形，‎ 所以，由平面，故 因为，所以平面. 取的中点，∵，∴， ∴四边形为平行四边形，所以 ‎ ‎∴平面．即为四等分点