高考数学复习课时提能演练(七十九) 选修4-5_1 8页

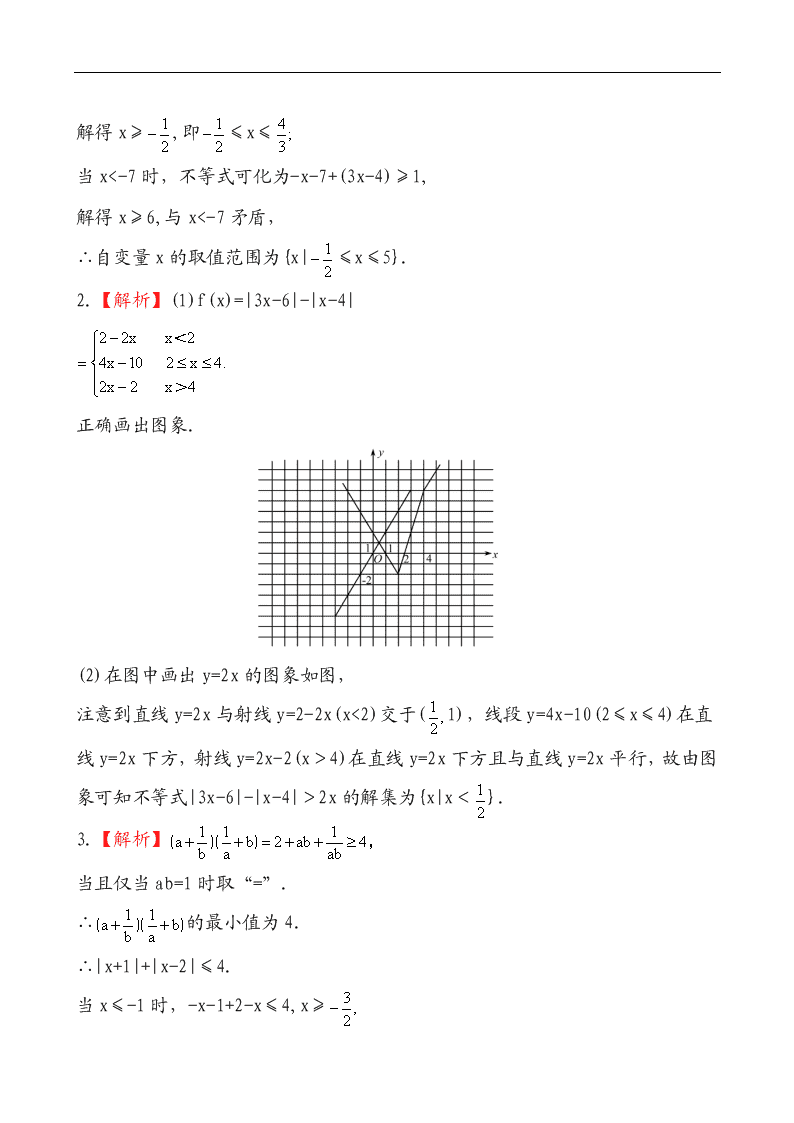
‎ ‎ 课时提能演练(七十九)‎ ‎1.(1)已知|2x-3|≤1的解集为［m,n］，求m+n的值；‎ ‎(2)若函数f(x)=2|x+7|-|3x-4|的最小值为2，求自变量x的取值范围.‎ ‎2.已知函数f(x)=|3x-6|-|x-4|.‎ ‎(1)作出函数y=f(x)的图象;‎ ‎(2)解不等式|3x-6|-|x-4|＞2x.‎ ‎3.已知关于x的不等式|x+1|+|x-2|≤对任意正实数a、b恒成立，求实数x的取值范围.‎ ‎4.(2011·福建高考)设不等式|2x-1|<1的解集为M.‎ ‎(1)求集合M；‎ ‎(2)若a,b∈M，试比较ab+1与a+b的大小.‎ ‎5.(2011·襄阳模拟)已知函数f(x)=|x+2|-|x-1|‎ ‎(1)解不等式f(x)>1;‎ ‎(2)g(x)=(a>0)‎ 若对s∈(0，+∞),t∈(-∞,+∞)，恒有g(s)≥f(t)，试求实数a的取值范围.‎ ‎6.(2012·哈尔滨模拟)已知函数f(x)=|x-a|.‎ ‎(1)若不等式f(x)≤m的解集为{x|-1≤x≤5},求实数a,m的值.‎ ‎(2)当a=2时，解关于x的不等式f(x)+t≥f(x+2t)(t≥0).‎ ‎7.(2011·新课标全国卷)设函数f(x)=|x-a|+3x,其中a>0.‎ ‎(1)当a=1时，求不等式f(x)≥3x+2的解集；‎ ‎(2)若不等式f(x)≤0的解集为{x|x≤-1}，求a的值.‎ ‎8.已知函数f(x)=|x-4|+|x+5|.‎ ‎(1)试求使等式f(x)＝|2x+1|成立的x的取值范围；‎ ‎(2)若关于x的不等式f(x)＜a的解集不是空集，求实数a的取值范围.‎ ‎9.已知函数f(x)=|2x+1|,g(x)=|x-4|.‎ ‎(1)求不等式f(x)>2的解集；‎ ‎(2)不等式f(x)-g(x)≥m+1的解集为R，求实数m的取值范围.‎ ‎10.已知f(x)=x|x-a|-2.‎ ‎(1)当a=1时，解不等式f(x)<|x-2|;‎ ‎(2)当x∈(0,1］时，f(x)<-1恒成立，求实数a的取值范围.‎ 答案解析 ‎1.【解析】(1)由不等式|2x-3|≤1得-1≤2x-3≤1‎ 得1≤x≤2，∴m=1,n=2,m+n=3.‎ ‎(2)依题意，2|x+7|-|3x-4|≥2,∴|x+7|-|3x-4|≥1,‎ 当x>时，不等式可化为x+7-(3x-4)≥1,‎ 解得x≤5,即0,‎ 故ab+1>a+b.‎ ‎5.【解析】(1)①当x<-2时，原不等式可化为-x-2+x-1>1，此时不成立；‎ ‎②当-2≤x≤1时，原不等式可化为x+2+x-1>1，即01时，原不等式可化为x+2-x+1>1恒成立,即x>1，‎ ‎∴原不等式的解集是(0，+∞).‎ ‎(2)因为g(s)≥f(t)恒成立，即g(s)的最小值不小于f(t)的最大值，‎ g(s)=‎ 由几何意义可知f(t)的最大值为3.‎ ‎∴2-3≥3,∴a≥3.‎ ‎6.【解析】(1)由|x-a|≤m得a-m≤x≤a+m,‎ 所以解之得为所求.‎ ‎(2)当a=2时，f(x)=|x-2|,‎ 所以f(x)+t≥f(x+2t)|x-2+2t|-|x-2|≤t ①‎ 当t=0时，不等式①恒成立，即x∈R;‎ 当t>0时，不等式①或或 解之得x<2-2t或2-2t≤x≤2-或x∈,‎ 即x≤2-;‎ 综上，当t=0时，原不等式的解集为R，‎ 当t>0时，原不等式的解集为{x|x≤2-}.‎ ‎7.【解题指南】第(1)问，将a=1代入函数f(x)的解析式，利用解绝对值不等式的公式求解；第(2)问f(x)≤0|x-a|+3x≤0,然后分x≥a和x0，所以不等式组的解集为{x|x≤}，‎ 由题设可得=-1,故a=2.‎ ‎8.【解析】(1)方法一：因为f(x)=|x-4|+|x+5|≥|(x-4)+(x+5)|=|2x+1|,‎ 当且仅当(x-4)(x+5)≥0,‎ 即x≤-5或x≥4时取等号，‎ 所以若f(x)=|2x+1|成立，‎ 则x的取值范围是(-∞,-5]∪[4,+∞).‎ 方法二：f(x)=|x-4|+|x+5|‎ 又|2x+1|=‎ 所以若f(x)=|2x+1|,‎ 则x的取值范围是(-∞,-5]∪[4,+∞).‎ ‎(2)方法一：因为f(x)=|x-4|+|x+5|≥|(x-4)-(x+5)|=9,‎ 所以若关于x的不等式f(x)＜a的解集非空，‎ 则a＞f(x)min=9,即a的取值范围是(9，+∞).‎ 方法二：由(1)方法二易知，f(x)min=9,‎ ‎∴a＞9,即a的取值范围是(9,+∞).‎ ‎9.【解析】(1)不等式f(x)>2等价于|2x+1|>2,‎ ‎∴2x+1>2或2x+1<-2，解得x>或x<.‎ ‎∴不等式f(x)>2的解集为{x|x>或x<}.‎ ‎(2)记y=f(x)-g(x)，则 由图可知，当x=-0.5时，y取最小值，且最小值为-4.5，‎ ‎∵不等式f(x)-g(x)≥m+1的解集为R，‎ ‎∴m+1≤-4.5,即m≤-5.5,‎ ‎∴实数m的取值范围为(-∞,-5.5］.‎ ‎10.【解析】(1)a=1时，f(x)<|x-2|,‎ 即x|x-1|-2<|x-2|.(﹡)‎ ‎①当x≥2时，由(﹡)x(x-1)-2