2014年高考试题——数学理（江西卷）原卷版 5页

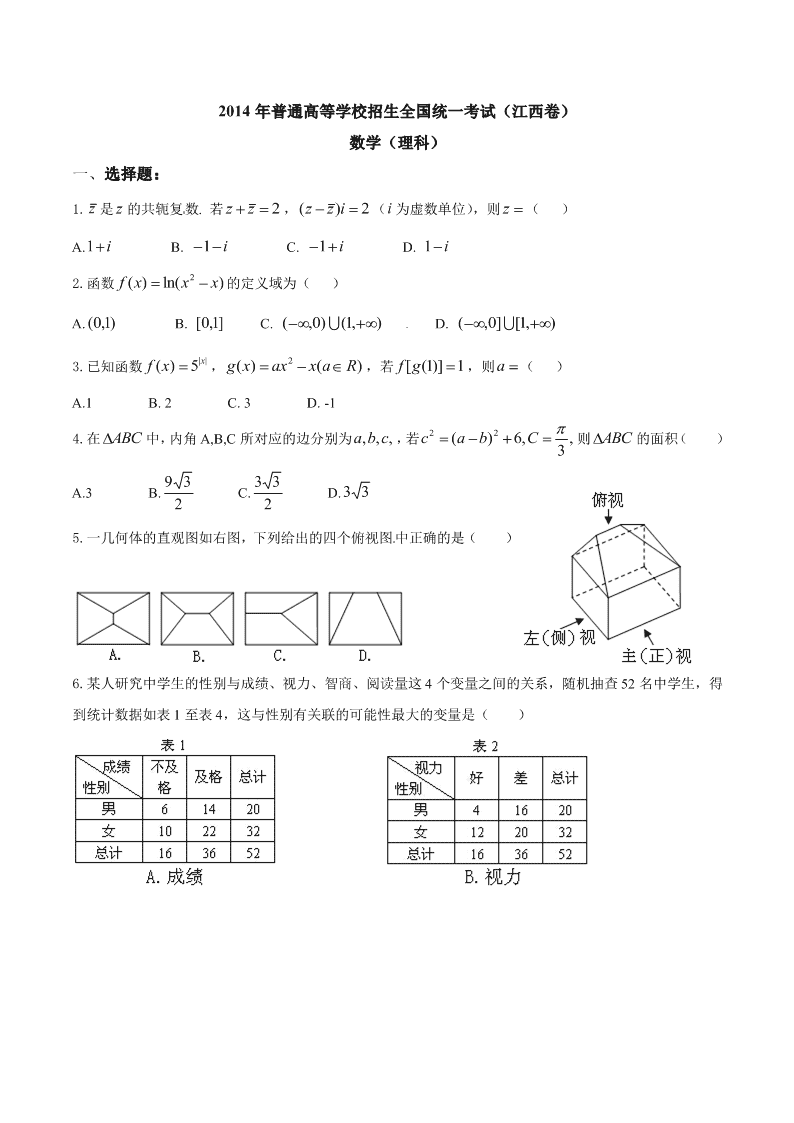
2014 年普通高等学校招生全国统一考试（江西卷） 数学（理科） 一、选择题： 1. z 是 z 的共轭复数. 若 2 zz ， 2)(  izz （i 为虚数单位），则 z （ ） A. i1 B. i1 C. i1 D. i1 2.函数 )ln()( 2 xxxf  的定义域为（ ） A. )1,0( B. ]1,0[ C. ),1()0,(   D. ),1[]0,(   3.已知函数 ||5)( xxf  ， )()( 2 Raxaxxg  ，若 1)]1([ gf ，则 a （ ） A.1 B. 2 C. 3 D. -1 4.在 ABC 中，内角 A,B,C 所对应的边分别为 ,,, cba ，若 ,3,6)( 22  Cbac 则 的面积（ ） A.3 B. 2 39 C. 2 33 D. 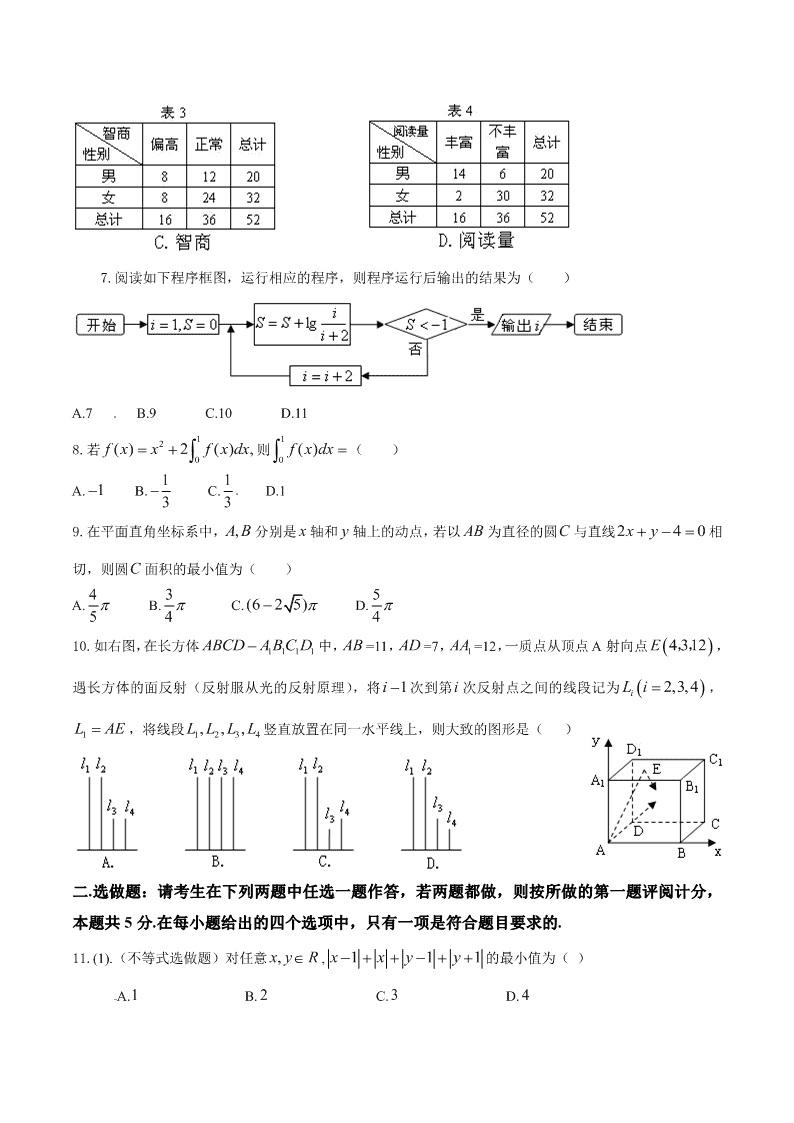33 5.一几何体的直观图如右图，下列给出的四个俯视图中正确的是（ ） 6.某人研究中学生的性别与成绩、视力、智商、阅读量这 4 个变量之间的关系，随机抽查 52 名中学生，得 到统计数据如表 1 至表 4，这与性别有关联的可能性最大的变量是（ ） 7.阅读如下程序框图，运行相应的程序，则程序运行后输出的结果为（ ） A.7 B.9 C.10 D.11 8.若 12 0 ( ) 2 ( ) ,f x x f x dx 则 1 0 ()f x dx  （ ） A. 1 B. 1 3 C. 1 3 D.1 9.在平面直角坐标系中， ,AB分别是 x 轴和 y 轴上的动点，若以 AB 为直径的圆C 与直线2 4 0xy   相 切，则圆C 面积的最小值为（ ） A. 4 5 B. 3 4 C.(6 2 5) D. 5 4  10.如右图，在长方体 1 1 1 1ABCD A B C D 中，AB =11，AD =7， 1AA =12，一质点从顶点 A 射向点  4 312E ，， ， 遇长方体的面反射（反射服从光的反射原理），将 1i  次到第i 次反射点之间的线段记为  2,3,4iLi ， 1L AE ，将线段 1 2 3 4, , ,L L L L 竖直放置在同一水平线上，则大致的图形是（ ） 二.选做题：请考生在下列两题中任选一题作答，若两题都做，则按所做的第一题评阅计分， 本题共 5 分.在每小题给出的四个选项中，只有一项是符合题目要求的. 11.(1).（不等式选做题）对任意 ,x y R , 1 1 1x x y y      的最小值为（ ） A.1 B. 2 C.3 D. 4 11.(2).（坐标系与参数方程选做题）若以直角坐标系的原点为极点， x 轴的非负半轴为极轴建立极坐标系， 则线段  1 0 1y x x    的极坐标为（ ） A. 1 ,0cos sin 2    B. 1 ,0cos sin 4    C. cos sin ,0 2        D. cos sin ,0 4        三、填空题 12.10 件产品中有 7 件正品，3 件次品，从中任取 4 件，则恰好取到 1 件次品的概率是________. 13.若曲线 xye 上点 P 处的切线平行于直线 2 1 0xy   ，则点 的坐标是________. 14.已知单位向量 1e 与 2e 的夹角为  ，且 1cos 3  ，向量 1232a e e与 123b e e的夹角为  ，则 cos = 15.过点 (1,1)M 作斜率为 1 2 的直线与椭圆C ： 22 221( 0)xy abab    相交于 ,AB，若 M 是线段 AB 的 中点，则椭圆 的离心率为 三、解答题 16.已知函数 ( ) sin( ) cos( 2 )f x x a x    ，其中 , ( , )22aR    （1）当 2, 4a 时，求 ()fx在区间[0, ] 上的最大值与最小值； （2）若 ( ) 0, ( ) 12ff ，求 ,a  的值. 17.（本小题满分 12 分） 已知首项都是 1 的两个数列 （ ），满足 . （1）令 ，求数列 的通项公式； （2）若 13n nb  ，求数列 的前 n 项和 18.（本小题满分 12 分） 已知函数 . （1）当 时，求 的极值；[来源:学*科*网 Z*X*X*K] （2）若 在区间 1(0, )3 上单调递增，求 b 的取值范围. 19.(本小题满分12分) 如图，四棱锥 ABCDP 中， ABCD 为矩形，平面 PAD 平面 . （1）求证： ;PDAB  （2）若 ,2,2,90  PCPBBPC  问 AB 为何值时，四棱锥 的体积最大？并求此时平面 PBC 与平面 DPC 夹角的余弦值. 20.（本小题满分 13 分） 如图，已知双曲线 )0(12 2 2  aya xCn 的右焦点 F ,点 BA, 分别在C 的两条渐近线上， xAF  轴， BFOBAB , ∥OA(O 为坐标原点）. （1）求双曲线C 的方程； （2）过 上一点 )0)(( 00,0 yyxP 的 直线 1: 02 0  yya xxl 与直线 AF 相交于点 M ，与直线 2 3x 相交于 点 N ，证明点 P 在C 上移动时， NF MF 恒为定值，并求此定值. 21.（满分 14 分）随机将  1,2, ,2 , 2n n N n   这 2n 个连续正整数分成 A,B 两组，每组 n 个数，A 组最 小数为 1a ，最大数为 2a ；B 组最小数为 1b ，最大数为 1b ，记 2 1 1 2,a a b b    （1）当 3n  时，求 的分布列和数学期望； （2）令 C 表示事件 与 的取值恰好相等，求事件 C 发生的概率  pc； 对（2）中的事件 C, c 表示 C 的对立事件，判断 和  pc 的大小关系，并说明理由。 [来源:学科网 ZXXK]