- 1.64 MB
- 2021-04-27 发布
湖南省岳阳县第一中学2019-2020学年高二上学期期中考试数学试卷
时量:120分钟 总分:150分
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)
1.为了了解某地区参加数学竞赛的名学生的成绩,计划采用系统抽样的方法从中抽取一个容量为的样本,则每个学生被抽到的概率为 ( )
A. B. C. D.
2.在中,“是直角三角形”是“”的 ( )
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
3.某车间为了规定工时定额,需要确定加工零件所花
加工零件数(个)
10
20
30
40
50
加工时间(分钟)
64
69
75
82
90
费的时间,为此进行了5次试验,收集数据如右.经
检验,这组样本数据具有线性相关关系,那么对于
加工零件的个数与加工时间这两个变量,下列
判断正确的是 ( )
A. 成正相关,其回归直线经过点(30,75) B. 成正相关,其回归直线经过点(30,76)
C. 成负相关,其回归直线经过点(30,76) D. 成负相关,其回归直线经过点(30,75)
4.采用系统抽样方法从人中抽取人做问卷调查,为此将他们随机编号 ,抽到的人中,编号落入区间的人做问卷,落入区间的做问卷,其余的人做问卷,则抽到的人中,做问卷的人数为 ( )
A. B. C. D.
5. 下列命题错误的是 ( )
A.对于命题 :,使得,则为,均有
B.“”是“”的充分不必要条件
C.若是假命题,则均为假命题
D.命题“若则”是正确的
6.已知中心在原点的双曲线的右焦点为,离心率等于,则的方程为 ( )
A. B. C. D.
7. 已知平面的一个法向量是,点在内,则到 的距离是 ( )
A、 B、8 C、3 D、10
8. 如图所示,在平行六面体中, 为
与的交点.若,则下列向量中与
相等的向量是 ( )
A. B. C. D.
9. 已知点,抛物线的焦点为,射线与抛物线相交于点,与其准线相交于点,则等于 ( )
A. B. C. D.
10. 已知椭圆的右焦点为,过点的直线交于 两点,若的中点坐标为,则的方程为 ( )
A. B. C. D.
11. 一张储蓄卡的密码共有位数字,每位数字都可以从中任选一个.某人在银行自助提款机上取钱时,忘记了密码最后一位数字,如果他记得密码的最后一位是偶数,则他不超过次就按对的概率是 ( )
A. B. C. D.
12. 过抛物线上一定点,作两条直线分别交抛物线于.当与的斜率存在且倾斜角互补时,的值为 ( ) A. B. C. D.无法确定
二.填空题( 本大题共4小题,每小题5分,共20分. 将答案填入答卷指定位置.)
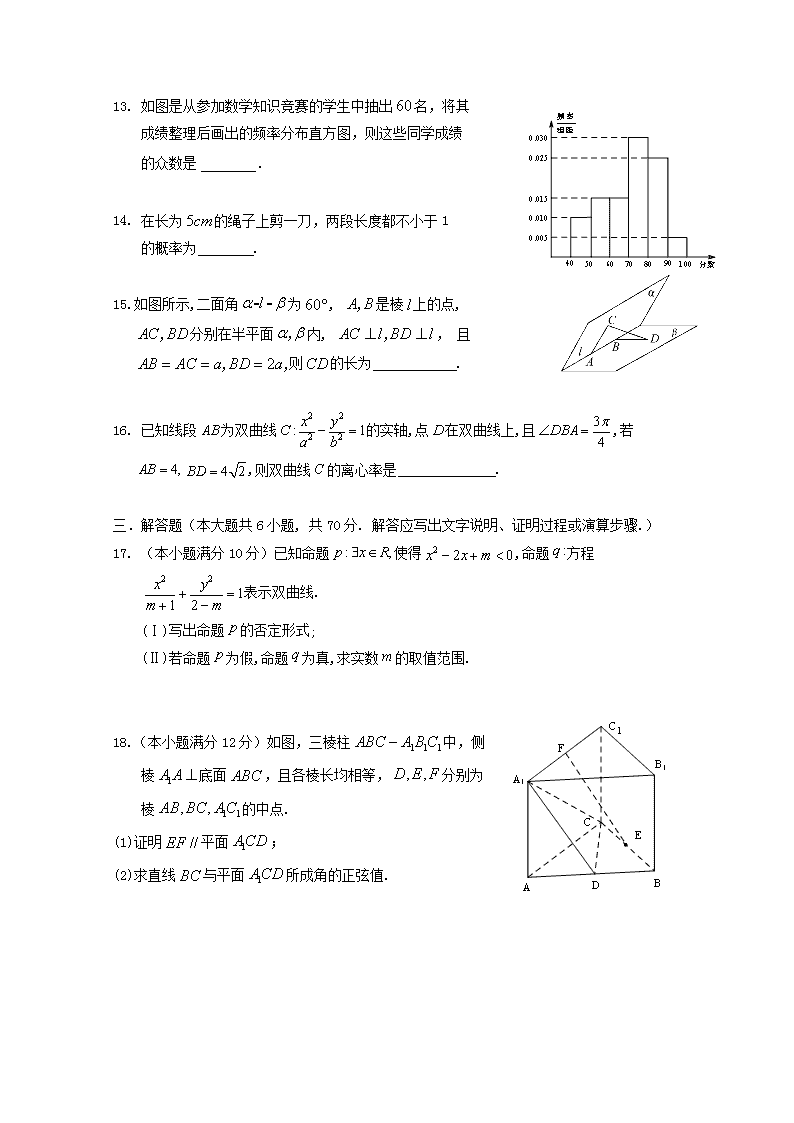
13. 如图是从参加数学知识竞赛的学生中抽出名,将其
成绩整理后画出的频率分布直方图,则这些同学成绩
的众数是.
14. 在长为的绳子上剪一刀,两段长度都不小于1
的概率为 .
15.如图所示,二面角为, 是棱上的点,
分别在半平面内, , 且
则的长为 .
16. 已知线段为双曲线的实轴,点在双曲线上,且,若,则双曲线的离心率是 .
三.解答题(本大题共6小题, 共70分. 解答应写出文字说明、证明过程或演算步骤.)
17. (本小题满分10分)已知命题使得,命题方程表示双曲线.
(Ⅰ)写出命题的否定形式;
(Ⅱ)若命题为假,命题为真,求实数的取值范围.
18.(本小题满分12分)如图,三棱柱中,侧
棱底面,且各棱长均相等,分别为
棱的中点.
(1)证明平面;
(2)求直线与平面所成角的正弦值.
19.(本小题满分12分)某产品的三个质量指标分别为,用综合指标
评价该产品的等级.若,则该产品为一等品.现从一批该产品中,随机抽取件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
(1)利用上表提供的样本数据估计该批产品的一等品率;
(2)在该样本的一等品中,随机抽取件产品,
①用产品编号列出所有可能的结果;
②设事件为“在取出的件产品中,每件产品的综合指标都等于”,求事件发生的概率.
20.(本小题满分12分)已知椭圆经过点,离心率为,
左、右焦点分别为.
求椭圆的方程;
若直线与椭圆交于两点,与以为直径的圆交于两点,且满足,求直线的方程.
21.(本小题满分12分)如图所示,四棱锥的底面为等腰梯形,
,对角线与交于点,
底面.
(Ⅰ)求证:;
(Ⅱ)若四棱锥的体积,
求二面角的平面角的正弦值.
22.(本小题满分12分)已知抛物线的焦点为,为抛物线上异于原点的任意一点,过点的直线交抛物线于另一点,交轴的正半轴于点,且有.当点的横坐标为时,为正三角形.
(1)求抛物线的方程;
(2)若直线,且和抛物线有且只有一个公共点,
(i)证明:直线过定点,并求出定点坐标;
(ii)的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
2019年下学期岳阳县一中高二期中考试
数学试卷
时量:120分钟 总分:150分 命题人:
一.选择题(本大题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求)
1. 为了了解某地区参加数学竞赛的名学生的成绩,计划采用系统抽样的方法从中抽取一个容量为的样本,则每个学生被抽到的概率为 ( A )
A. B. C. D.
2.在中, “是直角三角形”是“”的 ( B )
A.充分不必要条件 B必要不充分条件 C充要条件 D既不充分也不必要条件
加工零件数 (个)
10
20
30
40
50
加工时间 (分钟)
64
69
75
82
90
3.某车间为了规定工时定额,需要确定加工零件所花费的时间,为此进行了5次试验,收集数据如右.经检验,这组样本数据具有线性相关关系,那么对于加工零件的个数与加工时间这两个变量,下列判断正确的是 ( B )
A. 成正相关,其回归直线经过点(30,75) B. 成正相关,其回归直线经过点(30,76)
C. 成负相关,其回归直线经过点(30,76) D. 成负相关,其回归直线经过点(30,75)
4. 采用系统抽样方法从人中抽取人做问卷调查,为此将他们随机编号为,抽到的人中,编号落入区间的 人做问卷,落入区间的做问卷,其余的人做问卷,则抽到的人中,做问卷的人数为 ( C )
A. B. C. D.
5. 下列命题错误的是 ( D )
A.对于命题 :,使得,则为,均有
B.“”是“”的充分不必要条件
C.若是假命题,则均为假命题
D.命题“若则”是正确的
6.已知中心在原点的双曲线的右焦点为,离心率等于,则的方程( B )
A. B. C. D.
7. 已知平面的一个法向量是,点在内,则到的距离是 ( A )
A、 C、3 B、8 A、10
8. 如图所示,在平行六面体中, 为
与的交点.若,则下列向
量中与相等的向量是 ( A )
A. B. C. D.
9. 已知点,抛物线的焦点为,射线与抛物线相交于点,与其准线相交于点,则等于 ( C )
A. B. C. D.
10. 已知椭圆的右焦点为,过点的直线交于两点,若的中点坐标为,则的方程为 ( D )
A. B. C. D.
11. 一张储蓄卡的密码共有位数字,每位数字都可以从中任选一个.某人在银行自助提款机上取钱时,忘记了密码最后一位数字,如果他记得密码的最后一位是偶数,则他不超过次就按对的概率是 ( C )
A. B. C. D.
12. 过抛物线上一定点,作两条直线分别交抛物
线于.当与的斜率存在且倾斜角互补时,则的值为 ( B )
A. B. C. D.无法确定
二.填空题( 本大题共4小题,每小题5分,共20分. 将答案填入答卷指定位置.)
13. 如图是从参加低碳生活知识竞赛的学生中抽出名,将其成绩整理后画出的频率分布直方图,则这些同学成绩的众数是.
14.在长为的绳子上剪一刀,两段长度都不小于1的概率为 0.6 .
15.如图所示,二面角为, 是棱上的点, 分别在半平面内, , 且则的长为 .
16. 已知线段为双曲线的实轴,点在双曲线上,且,若,则双曲线的离心率是 .
三.解答题(本大题共6小题, 共70分. 解答应写出文字说明、证明过程或演算步骤.)
17. (本小题满分10分)已知命题使得,命题方程表示双曲线.
(Ⅰ)写出命题的否定形式;
(Ⅱ)若命题为假,命题为真,求实数的取值范围.
【解】(Ⅰ)命题的否定形式:
,都有.………………………………………………………5分
(Ⅱ)由为假,即为真,所以,即;
又命题为真,则有,即或;
所以假、真时,,即求.………………………………………………………10分
18.(本小题满分12分)如图,三棱柱中,侧棱底面,且各棱长均相等,分别为棱的中点.
(1)证明平面;
(2)求直线与平面所成角的正弦值.
解析:(1)连接,易知且,所以是平行四边形,所以,又在平面外,所以平面; …………………6分
(2) …………………12分
19.(本小题满分12分)某产品的三个质量指标分别为,用综合指标评价该产品的等级.若,则该产品为一等品.现从一批该产品中,随机抽取件产品作为样本,其质量指标列表如下:
产品编号
质量指标
产品编号
质量指标
利用上表提供的样本数据估计该批产品的一等品率;
在该样本的一等品中,随机抽取件产品,
①用产品编号列出所有可能的结果;
②设事件为“在取出的件产品中,每件产品的综合指标都等于”,求事件发生的概率.
解析:(1)
…………………………5分
(2)①该样本中一等品中,随机抽取件产品的所以可能结果为
…………………………8分
②这批样品中综合指标为有,则事件发生的可能结果为共种, ……………12分
20.(本小题满分12分)已知椭圆经过点,离心率为,左、右焦点分别为.
求椭圆的方程;
若直线与椭圆交于两点,与以为直径的圆交于两点,且满足,求直线的方程.
解答:(1)根据题意,,………………………………… ……………………1分
又离心率,所以…………………………………………………3分
所以椭圆的方程为 ……………………………………………………5分
(2)设,联立直线与椭圆的方程可得,
………………………………………6分
因此, ………………………………7分
根据垂径定理,可得,………………………8分
由已知,可得…………………………………10分
解得,因此直线的方程为………………………………12分
21.(本小题满分12分)如图所示,四棱锥的底面为等腰梯形,
,对角线与交于点,
底面.
(Ⅰ)求证:;
(Ⅱ)若四棱锥的体积,求二面角的平面角的正弦值.
【解】(Ⅰ)证明 在等腰梯形中,知,
又,所以,故,
即,又底面,得,
且,所以面,即.………………………………………5分
B
C
O
S
A
H
D
x
y
z
(Ⅱ)由,
于是,得.
法一 由两两垂直,故以为原点,
分别以为轴建系如图;
则,
,
设平面的法向量为,则由
得,令,得,即
同理可得平面的一个法向量为,设二面角的平面角为,
则,
又,故.……………………………………………12分
B
C
O
S
A
H
D
x
y
z
法二 过点作于点,连接,则
由知面,
所以(三垂线定理)
所以为二面角的平面角.
由等面积知,
故,,
由余弦定理有,
即,即求.
22.(本小题满分12分)已知抛物线的焦点为,为抛物线上异于原点的任意一点,过点的直线交抛物线于另一点,交轴的正半轴于点,且有.当点的横坐标为时,为正三角形.
(1)求抛物线的方程;
(2)若直线,且和抛物线有且只有一个公共点,
(i)证明:直线过定点,并求出定点坐标;
(ii)的面积是否存在最小值?若存在,请求出最小值,若不存在,请说明理由.
解析::(1)由题意知当点的横坐标为时,不妨设设,则点的纵坐标为 ……………2分因此, (舍去) 所以抛物线的方程为 …………………4分
(2)①证明:由(1)知.
设
因为,则,
由得,故.
故直线的斜率 …………5分
因为直线和直线平行,
设直线的方程为,
代入抛物线方程得,
由题意,得 ………………6分
设,则,.
当时,,
可得直线的方程为, ………………7分
由,
整理可得,
直线恒过点F(1,0).
当时,直线的方程为,过点.
所以直线过定点 ………………8分
②由①知,直线过焦点,
所以.
设直线的方程为,
因为点)在直线上,
故. ………………9分
设.
直线的方程为,由,得
代入抛物线方程得,
所以,
可求得,. ………………10分
所以点到直线的距离为
则的面积
当且仅当,即时,等号成立.
所以的面积的最小值为. ……………12分