- 240.50 KB
- 2021-04-27 发布
高一下学期期末考试数学试题
一、选择题(每小题5分,共10小题)
1、直线的倾斜角为 ( )
A.30º B.60º C.120º D. 150º
2.已知等差数列满足,,则等于( )
A.90 B.95 C.170 D.340
3.设,,则下列不等式成立的是( )。
A. B. C. D.
4.直线与圆相切,则的值为( )
A.或 B. C. D.
5.若圆心坐标为(2,-1)的圆在直线上截得的弦长为,则这个
圆的方程是( )
A. B.
C. D.
6.已知点(3,1)和(- 4,6)在直线的两侧,则的取值范围是( )
A. <-7或>24 B. =7或=24 C. -7<<24 D. -24<<7
7. ,b,c表示直线,M表示平面,给出下列四个命题:①若∥M,b∥M,则∥b;②若bM,∥b,则∥M;③若⊥c,b⊥c,则∥b;④若⊥M,b⊥M,则∥b.其中正确命题的个数有( )
A.0个 B.1个 C.2个 D.3个
8. ABC中, ,则三角形的最小内角是( )
A. B. C. D.以上答案都不对
9.在中,若,则此三角形为( )
A.等腰三角形 B.直角三角形 C.等腰直角三角形 D.等腰或直角三角形
10.方程有两个不等实根,则k的取值范围是( )
A. B. C. D.
二、填空题(每小题5分,共6小题)
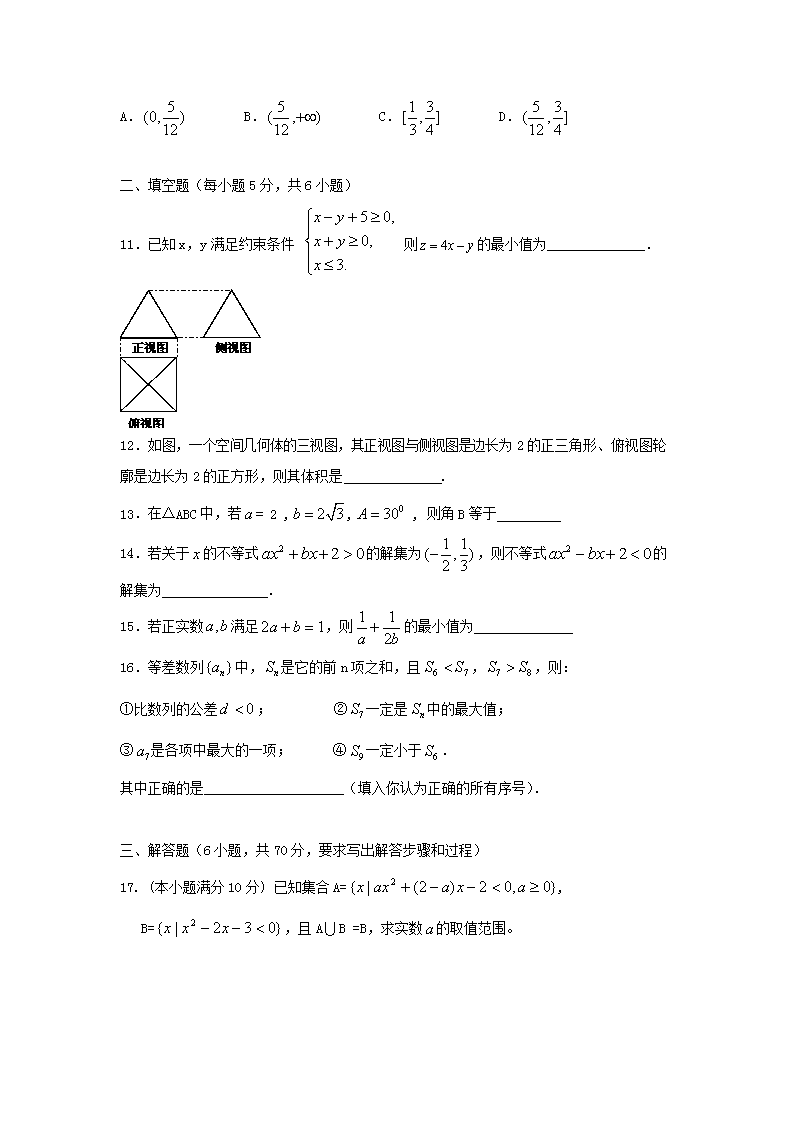
11.已知x,y满足约束条件 则的最小值为______________.
12.如图,一个空间几何体的三视图,其正视图与侧视图是边长为2的正三角形、俯视图轮廓是边长为2的正方形,则其体积是 .
13.在△ABC中,若= 2 ,, , 则角B等于
14.若关于的不等式的解集为,则不等式的解集为 .
15.若正实数满足,则的最小值为
16.等差数列中,是它的前n项之和,且,,则:
①比数列的公差; ②一定是中的最大值;
③是各项中最大的一项; ④一定小于.
其中正确的是____________________(填入你认为正确的所有序号).
三、解答题(6小题,共70分,要求写出解答步骤和过程)
17. (本小题满分10分) 已知集合A=,
B=,且AB =B,求实数的取值范围。
18. (本小题满分10分)直线和轴,轴分别交于点,在线段为边在第一象限内作等边△,如果在第一象限内有一点使得△和△的面积相等。
(1)求的值。 (2)求点C坐标。
20.(本小题满分12分)在中,的面积为,且.
(1)若且,求的值;
(2)若,求的最大值.
21.(本小题满分12分)如图,甲船以每小时海里的速度向正北方向航行,乙船按固定方向匀速直线航行,当甲船位于处时,乙船位于甲船的北偏西的方向处,此时两船相距20海里。当甲船航行20分钟到达处时,乙船航行到甲船的北偏西方向的处,此时两船相距海里,问乙船每小时航行多少海里?
22.(本小题满分14分)设数列的前项和为,若对于任意的正整数都有.
(1)设,求证:数列是等比数列。
(2)求数列的前项和.
(3)若实数使得恒成立,求的取值范围。
三、解答题
17.解:
(1)a=0时,不满足
(2)a>0 时, ,因为AB =B,所以,所以,
综上,
18.解:(1)由已知可得直线,设的方程为
则,过
得
(2),所以线段AB的中垂线为,与PC联立得,
所以。
19、证明:(1)连结,设
连结, 是正方体 是平行四边形
且
又分别是的中点,且
是平行四边形
面,面
面
(2)面
又,
同理可证, 又 面
20.解:(1)若且,由得:,∴ ,
∴ ,∴ .
(2)∵ ,∴
∵ , ∴ ,∴ ,(当且仅当时取等号)
∴ ,∴ .
21.解:如图所示,连结A1B2,由已知A2B2=,
因此,乙船的速度的大小为×60=(海里/小时).
答 乙船每小时航行海里.
22.解:(1)对于任意的正整数都成立,
两式相减,得
∴, 即,
由已知得 即
∴首项,即对一切正整数都成立。
∴数列是等比数列。
。。