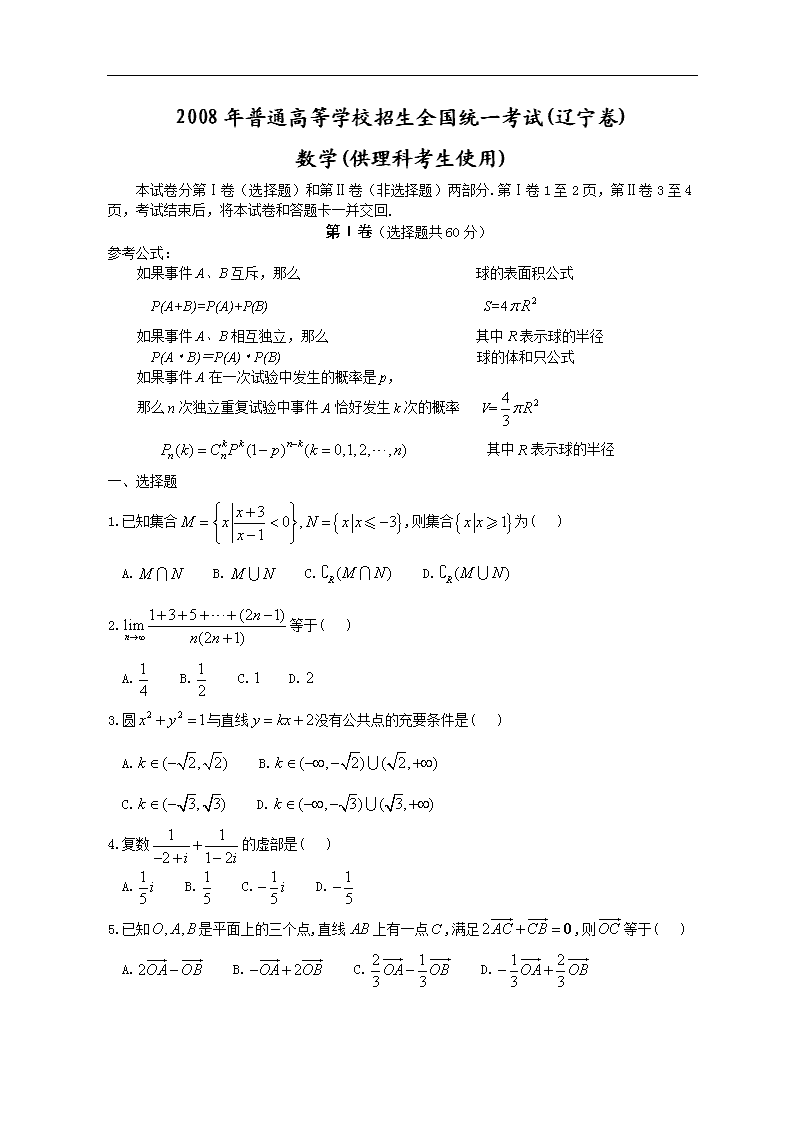人教新课标A版数学高三高考卷 08届 普通高等学校招生全国统一考试数学（辽宁卷·理科）（附答案，完全word版） 9页

2008 年普通高等学校招生全国统一考试(辽宁卷) 数学(供理科考生使用) 本试卷分第Ⅰ卷（选择题）和第Ⅱ卷（非选择题）两部分.第Ⅰ卷 1 至 2 页，第Ⅱ卷 3 至 4 页，考试结束后，将本试卷和答题卡一并交回. 第Ⅰ卷（选择题共 60 分） 参考公式： 如果事件 A、B 互斥，那么 球的表面积公式 P(A+B)=P(A)+P(B) S=4 2R 如果事件 A、B 相互独立，那么 其中 R 表示球的半径 P(A·B)＝P(A)·P(B) 球的体和只公式 如果事件 A 在一次试验中发生的概率是 p， 那么 n 次独立重复试验中事件 A 恰好发生 k 次的概率 V= 24 3 R ( ) (1 ) ( 0,1,2, , )k k n k n nP k C P p k n    其中 R 表示球的半径 一、选择题 1.已知集合  3 0 , 31 xM x N x xx         „ ,则集合 1x x … 为( ) A. M N B. M N C. ( )R M Nð D. ( )R M Nð 2. 1 3 5 (2 1)lim (2 1)n n n n        等于( ) A. 1 4 B. 1 2 C.1 D. 2 3.圆 2 2 1x y  与直线 2y kx  没有公共点的充要条件是( ) A. ( 2, 2)k   B. ( , 2) ( 2, )k     C. ( 3, 3)k   D. ( , 3) ( 3, )k     4.复数 1 1 2 1 2i i    的虚部是( ) A. 1 5 i B. 1 5 C. 1 5 i D. 1 5  5.已知 , ,O A B 是平面上的三个点,直线 AB 上有一点C ,满足 2AC CB  0   ,则OC  等于( ) A. 2OA OB  B. 2OA OB   C. 2 1 3 3OA OB  D. 1 2 3 3OA OB   6.设 P 为曲线 2: 2 3C y x x   上的点,且曲线C 在点 P 处切线倾斜角的取值范围是[0, ]4  ,则 点 P 横坐标的取值范围是( ) A. 1[ 1, ]2   B.[ 1,0] C.[0,1] D. 1[ ,1]2 7.4 张卡片上分别写有数字 1,2,3,4,从这 4 张卡片中随机抽取 2 张,则取出的 2 张卡片上的数字 之和为奇数的概率为( ) A. 1 3 B. 1 2 C. 2 3 D. 3 4 8.将函数 2 1xy   的图象按向量 a 平移得到函数 12xy  的图象,则 a 等于( ) A. ( 1, 1)  B. (1, 1) C. (1,1) D.( 1,1) 9.生产过程有 4 道工序,每道工序需要安排一人照看,现从甲乙丙等 6 名工人中安排 4 人分别照看 一道工序,第一道工序只能从甲乙两工人中安排 1 人,第四道工序只能从甲丙两工人中安排 1 人, 则不同的安排方案有( ) A.24 种 B.36 种 C.48 种 D.72 种 10.已知点 P 是抛物线 2 2y x 上的一个动点,则点 P 到点 (0,2) 的距离与 P 到该抛物线准线的距 离之和的最小值为( ) A. 17 2 B.3 C. 5 D. 9 2 11.在正方体 1 1 1 1ABCD A B C D 中, ,E F 分别为棱 1 1,AA CC 的中点,则在空间中与三条直线 1 1, ,A D EF CD 都相交的直线( ) A.不存在 B.有且只有两条 C.有且只有三条 D.有无数条 12.设 ( )f x 是连续的偶函数,且当 0x  时 ( )f x 是单调函数,则满足 3( ) ( )4 xf x f x   的所有 x 之 和为( ) A. 3 B.3 C. 8 D.8 第Ⅰ卷（选择题共 60 分） 二、填空题 13.函数 1, 0 , 0x x xy e x     … 的反函数是____________________. 14.在体积为 4 3 的球的表面上有 , ,A B C 三点, 1, 2, ,AB BC A C  两点的球面距离为 3 3  ,则球心到平面 ABC 的距离为______________. 15.已知 2 3 1(1 )( ) nx x x x    的展开式中没有常数项, *,2 8n N n „ „ ,则 n  ______. 16.已知 ( ) sin( ) ( 0), ( ) ( )3 6 3f x x f f       ,且 ( )f x 在区间 ( , )6 3   有最小值,无最大值, 则  __________. 三、解答题 17.在 ABC△ 中,内角 , ,A B C 对边的边长分别是 , ,a b c .已知 2, 3c C   . ⑴若 ABC△ 的面积等于 3 ,求 ,a b ; ⑵若sin sin( ) 2sin 2C B A A   ,求 ABC△ 的面积. 18.某批发市场对某种商品的周销售量(单位:吨)进行统计,最近 100 周的统计结果如下表所示: 周销售量 2 3 4 频数 20 50 30 ⑴根据上面统计结果,求周销售量分别为 2 吨,3 吨和 4 吨的频率; ⑵已知每吨该商品的销售利润为 2 千元, 表示该种商品两周销售利润的和(单位:千元),若以上 述频率作为概率,且各周的销售量相互独立,求 的分布列和数学期望. 19. 如 图 , 在 棱 长 为 1 的 正 方 体 ABCD A B C D    中 , (0 1)AP BQ b b    , 截 面 PQEF A D∥ ,截面 PQGH AD∥ . ⑴证明:平面 PQEF 和平面 PQGH 互相垂直; ⑵证明:截面 PQEF 和截面 PQGH 面积之和是 定值,并求出这个值; ⑶若 D E 与平面 PQEF 所成的角为 45 ,求 D E 与平面 PQGH 所成角的正弦值. 20.在直角坐标系 xOy 中,点 P 到两点 (0, 3),(0, 3) 的距离之和为4,设点 P 的轨迹为C ,直线 1y kx  与C 交于 ,A B 两点. ⑴写出 C 的方程; ⑵若OA OB  ,求 k 的值; ⑶若点 A 在第一象限,证明:当 0k  时,恒有 OA OB  . 21.在数列   ,n na b 中, 1 12, 4a b  ,且 1, ,n n na b a  成等差数列, 1 1, ,n n nb a b  成等比数列. A B CD A B CD P Q EF GH ⑴求 2 3 4, ,a a a 及 2 3 4, ,b b b ,由此猜测   ,n na b 的通项公式,并证明你的结论; ⑵证明: 1 1 2 2 1 1 1 5 12n na b a b a b       . 22.设函数 ln( ) ln ln( 1)1 xf x x xx     . ⑴求 ( )f x 的单调区间和极值; ⑵是否存在实数 a ,使得关于 x 的不等式 ( )f x a… 的解集为 (0, ) ?若存在,求 a 的取值范围;若 不存在,试说明理由. 2008 年普通高等学校招生全国统一考试（辽宁卷） 数学（供理科考生使用）试题参考答案和评分参考 说明： 一、 解答指出了每题要考查的主要知识和能力，并给出了一种或几种解决供参考，如果考生 的解法与本解答不同，可根据试题的主要考查内容比照评分标准制订相应的评分细则. 二、对解答题，当考生的解答在某一步出现错误时，如果后继部分的解答未改变该题的内容和难 度，可视影响的程度决定后继部分的给分，但不得超过该部分正确解答应得分数的一半；如果后 继部分的解答有较严重的错误，就不再给分. 三、答右端所注分数，表示考生正确做到这一步应得的累加分数. 四、只给整数分数，选择题和填空题不给中间分. 一、选择题：本题考查基本知识和基本运算，每小题 5 分，共 60 分. （1）D （2）B （3）C （4）B （5）A （6）A （7）C （8）A （9）B （10）A （11）D （12）C (18)本小题主要考查频率、概率、数学期望等基础知识，考查运用概率知识解决实际问题的 能力.满分 12 分。 解：（Ⅰ）周销售量为 2 吨，3 吨和 4 吨的频率分别为 0.2,0.5 和 0.3. ……3 分 （Ⅱ） 的可能值为 8，10，12，14，16，且 P（ =8）=0.22=0.04, P（ =10）=2×0.2×0.5=0.2, P（ =12）=0.52+2×0.2×0.3=0.37, P（ =14）=2×0.5×0.3=0.3, P（ =16）=0.32=0.09.  的分布列为  8 10 12 14 16 P 0.04 0.2 0.37 0.3 0.09 ……9 分 F =8×0.04+10×0.2+12×0.37+14×0.3+16×0.09=12.4 千元） ……12 分 （19）本小题主要考查空间中的线面关系，面面关系，解三角形等基础知识，考查空间想象 能力与逻辑能力，满分 12 分。 解法一： （I）证明：在正方体中，AD′  A′D,AD′⊥AB,又由已知可得 PF∥A′D，PH∥AD′,PQ∥AB, 所以 PH⊥PF,PH⊥PQ, 所以 PH⊥平面 PQEF. 所以平面 PQEF 和平面 PQGH 互相垂直， ……4 分 （Ⅱ）证明：由（Ⅰ）知 2 , 2 'PF AP PH PA  ，又截面 PQEF 和截面 PQCH 都是矩形，且 PQ=1，所以截面 PQEF 和截面 PQCH 面积之和是 ( 2 2 ') 2AP PA PQ   ，是定值. 8 分 （III）解：连结 BC′交 EQ 于点 M. 因为 PH∥AD′,PQ∥AB, 所以平面 ABC′D′和平面 PQGH 互相平行，因此 D′E 与平面 PQGH 所成角与 D′E 与平面 ABC′D′所成角相等. 与（I）同理可证 EQ⊥平面 PQGH，可知 EM⊥平面 ABC′D′，因此 EM 与 D′E 的比值就 是所求的正弦值. 设 AD′交 PF 于点 N，连结 EN，由 FD=l-b 知 2 2 2' (1 ) 2, ' (1 ).2 2D E b ND b      因为 AD′⊥平面 PQEF，又已知 D′E 与平面 PQEF 成 45 角， 所以 D′E= 2 'ND 即 22 22 (1 ) (1 ) 22 2 b b          ， 解得 1 2b  ,可知 E 为 BC 中点. 所以 EM= 2 4 ，又 D′E= 2 3(1 ) 2 2b   ， 故 D′E 与平面 PQCH 所成角的正弦值为 2 ' 6 EM D E  . 解法二： 以 D 为原点，射线 DA、DC，DD′分别为 x,y,z 轴的正半轴建立如图的空间直角坐标系 D-xyz 由 已知得 DF-l-b，故 A（1，0，0），A′（1，0，1），D（0，0，0），D′（0，0，1）， P（1，0，b）,Q(1,1,b),E(1,-b,1,0), F(1-b,0,0),G(b,1,1),H(b,0,1). （I）证明：在所建立的坐标系中，可得 (0,1,0), ( ,0, ), ( 1,0,1 ). PQ PF b b PH b b           ' ( 1,0,1), ( 1,0, 1).AD AD      因为 ' '0, ' 0,AD PQ AD PF AD        所以 是平面 PQEF 的法向量. 因为 是平面 PQGH 的法向量. 因为 ' ' 0£ ¬ ' 'AD A D A D AD     所以 ， 所以平面 PQEF 和平面 PQGH 互相垂直 ……4 分 （II）证明：因为 (0, 1,0)EF  ，所以 , ,EF PQ EF PQ PF PQ        又 ，所以 PQEF 为矩形， 同理 PQGH 为矩形. 在所建立的坐标系中可求得| | 2(1 ) | | 2 ,PH B PF b    所以| | | | 2, | | 1PH PF PQ    又 ， 所以截面 PQEF 和截面 PQCH 面积之和为 2 ，是定值. 8 分 （III）解：由已知得 ' 'D E AD  与 成45 角,又 ' (1 , , 1), ' ( 1,0,1),D E b l AD      可得 2 ' ' 2 2 2| ' || ' | 2 (1 ) 2 D E AD b D E AD b         ， 即 2 2 11, .2(1 ) 2 b b b      解得 所以 1' ( ,1, 1), ' ( 1,0, 1)£ ¬2D E A D     又 所以D′E 与平面 PQGH 所成角的正弦值 为 1 1 22|cos ' , ' | .3 622 D E A D          ……12 分 （20）本小题主要考查平面向量，椭圆的定义、标准方程及直线与椭圆位置关系等基础知识，考 查综合运用解析几何知识解决问题的能力.满分 12 分. 解： （Ⅰ）设 P（x,y）,由椭圆定义可知，点 P 的轨迹 C 是以 (0, 3),(0, 3) 为焦长，长半轴 为 2 的椭圆.它的短半轴 2 22 ( 3) 1,b    故曲线 C 的方程为 22 4; 1.yx  ……3 分 （Ⅱ）设 1 1 2 2( , ), ( , )A x y B x y ，其坐标满足 2 2 1,4 1. yx y kx       消去 y 并整理得 2 2( 4) 2k x kx  3.0， 故 1 2 1 22 2 2 3, .4 4 kx x x xk k      ……5 分 若 ,OA OB  即 1 2 1 2 0.x x y y  面 2 2 1 2 1 2 2 2 2 3 3 2 1 0,4 4 4 k kx x y y k k k          化简得 24 1 0,k   所以 1 .2k   ……8 分 （Ⅲ） 2 2 2 2 2 2 1 1 2 2;( )OA OB x y x y     ＝ 2 2 2 2 1 2 2 2( ) 4(1 1 )x x x x     ＝ 1 2 1 23( )( )x x x x   ＝ 1 2 2 6 ( ) .4 k x x k   因为 A 在第一象限，故 x1＞0.由 1 2 2 3 4x x k   知 2 0,x  从而 1 2 0.x x  又 0,k  故 2 2 0,OA OB   即在题设条件下，恒有 .OA OB    ……12 分 （21）本小题主要考查等差数列，等比数例，数学归纳法，不等式等基础知识，考查综合运用数 学知识进行归纳、总结、推理、论证等能力.满分 12 分. 解： （Ⅰ）由条件得 2 1 1 12 , .n n n a n nb a a a b b     由此可得 2 2 2 3 4 46, 9, 12, 16, 20, 25.a b a b a b      ……2 分 猜测 2( 1), ( 1) .n na n n b n    ……4 分 用数学归纳法证明： ①当 n=1 时，由上可得结论成立. ②假设当 n=k 时，结论成立，即 2( 1), ( 1) ,k ka k k b k    那么当 n=k+1 时， 2 2 22 1 12 2( 1) ( 1) ( 1)( 2), ( 2)b k k k k k aa b a k k k k k b kb               所以当 n=k+1 时，结论也成立. 由①②，可知 2( 1), ( 1)n na n n b n   对一切正整数都成立. ……7 分 （Ⅱ） 1 2 1 1 5 .6 12a b   n≥2 时，由（Ⅰ）知 ( 1)(2 1) 2( 1) .n na b n n n n     ……9 分 故 1 1 2 2 1 1 1 1 1 1 1 1( )6 2 2 3 3 4 ( 1)n na b a b a b n n               ＝ 1 1 1 1 1 1 1 1( )6 2 2 3 3 4 1n n         ＝ 1 1 1 1 1 1 5( ) .6 2 2 1 6 4 12n      综上，原不等式成立. ……12 分