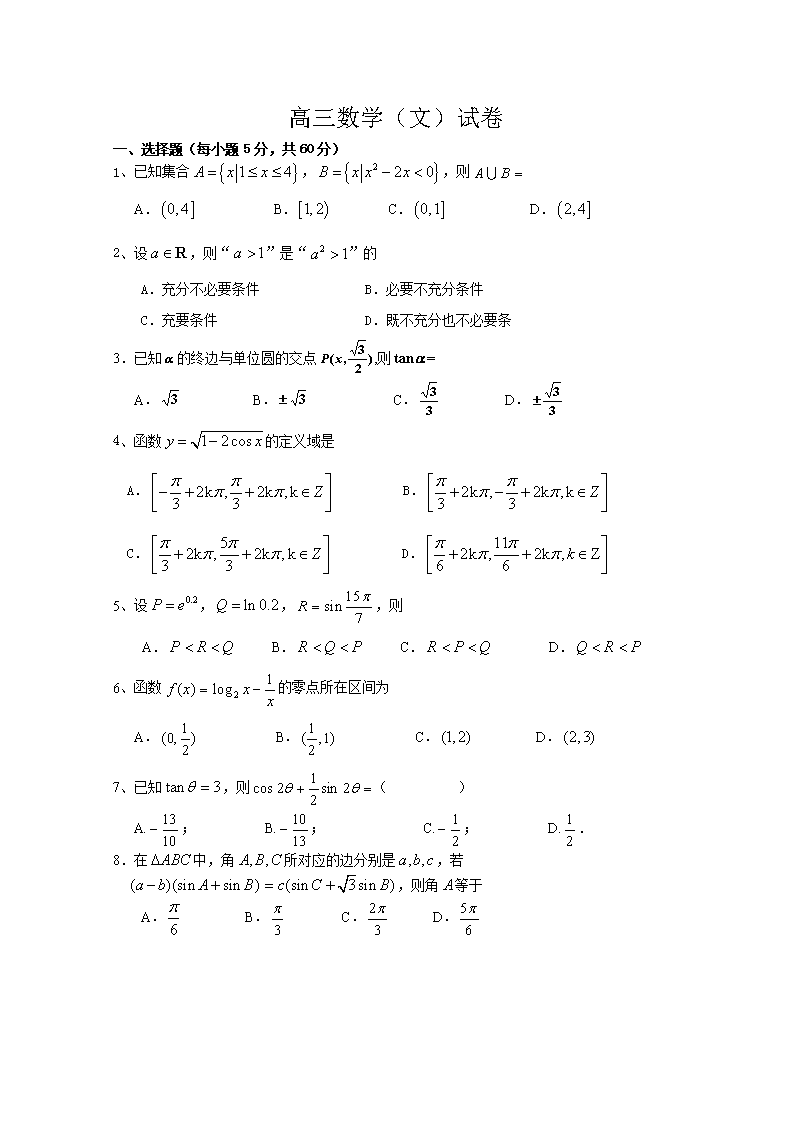宁夏银川市宁夏大学附中2020届高三上学期月考数学（文）试卷 4页

高三数学（文）试卷 一、选择题（每小题5分，共60分）‎ ‎1、已知集合，，则 ‎ A． B． C． D．‎ ‎2、设，则“”是“”的 ‎ A．充分不必要条件 B．必要不充分条件 ‎ C．充要条件 D．既不充分也不必要条 ‎3．已知的终边与单位圆的交点,则=‎ A． B． C． D．‎ ‎4、函数的定义域是 ‎ A． B．‎ ‎ C． D．‎ ‎5、设，，，则 A． B． C． D．‎ ‎6、函数的零点所在区间为 ‎ A． B． C． D．‎ ‎7、已知，则（ ）‎ ‎ A.； B.； C.； D.．‎ ‎8．在中，角所对应的边分别是，若，则角等于 A． B． C． D．‎ ‎9、已知函数的部分如图所示，将函数的图像向右平移个单位，再将各点的横坐标伸长为原来的2倍纵坐标不变，得到函数的图像，则函数的解析式为 A. B. ‎ C. D. 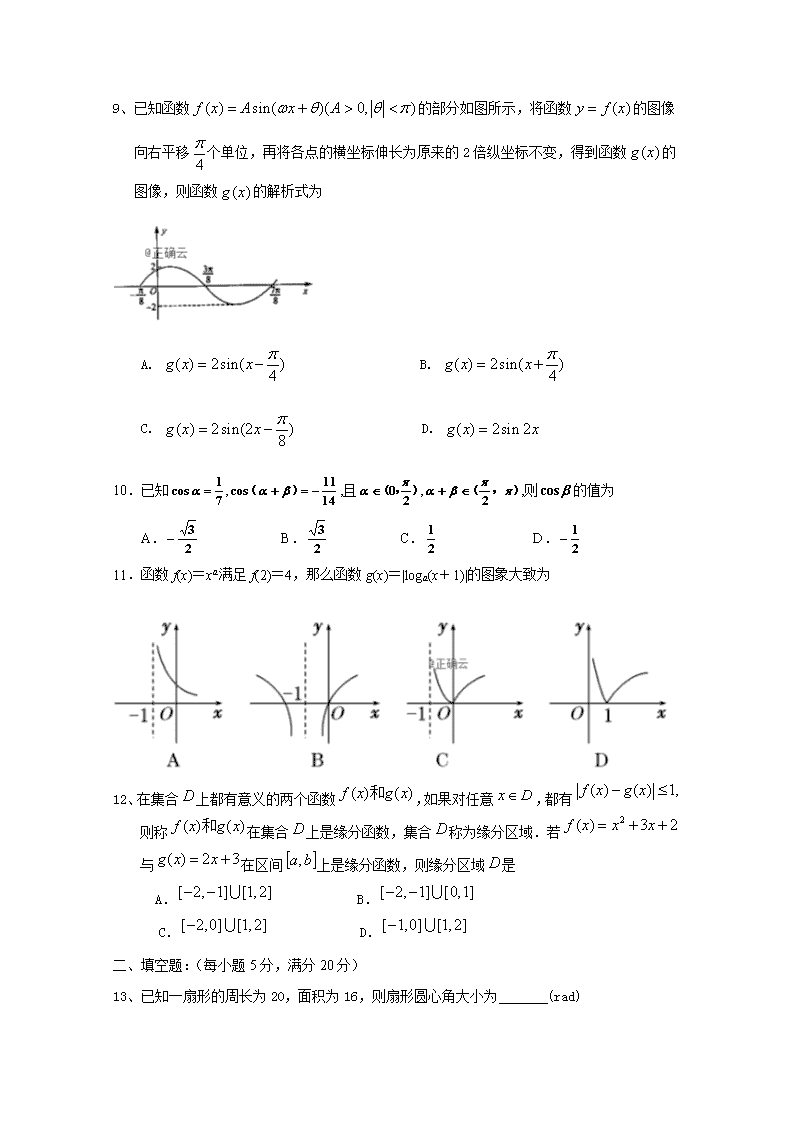‎ ‎10．已知,,且,,则的值为 A． B． C． D．‎ ‎11．函数f(x)＝xa满足f(2)＝4，那么函数g(x)＝|loga(x＋1)|的图象大致为 ‎12、在集合上都有意义的两个函数，如果对任意，都有则称在集合上是缘分函数，集合称为缘分区域．若与在区间上是缘分函数，则缘分区域是 ‎ A． B．  ‎ ‎ C． D． ‎ 二、填空题：（每小题5分，满分20分）‎ ‎13、已知一扇形的周长为20，面积为16，则扇形圆心角大小为 (rad) ‎ ‎14、已知：在上是奇函数且满足，当时，，则________．‎ ‎15．已知是(-∞,+∞)上的增函数，那么实数a的取值范围是______． ‎ ‎16、关于函数有下列命题：‎ ‎①函数的周期为；②直线是的一条对称轴；③点是的图像的一个对称中心；④将的图像向左平移个单位，可得到的图像。其中真命题的序号是 。（把你认为真命题的序号都写上）‎ 三、 解答题（解答应写出文字说明，证明过程或演算步骤。）‎ ‎17、（12分）已知函数的相邻两条对称轴之间的距离为．‎ ‎ （1）求的值；‎ ‎ （2）当时，求函数的值域.‎ ‎18、（12分）已知中的内角对边分别为，，。‎ ‎（1）若，求；‎ ‎（2）若，求的面积。‎ ‎19、（12分）已知（，）。‎ ‎（1）若函数的图象过且只有一个零点，求的表达式；‎ ‎（2）在（1）的条件下，当时，是单调函数，求的取值范围。‎ ‎20、（12分）已知函数 ‎（1）求函数的最小值及单调增区间；‎ ‎（2）若不等式在上恒成立，求实数的取值范围。‎ ‎21.（本小题满分12分）‎ 已知函数 ‎（1）若函数过点，求曲线在点处的切线方程；‎ ‎（2）求函数在区间上的最大值；‎ ‎22．(本小题满分10分)选修4－4：坐标系与参数方程 在平面直角坐标系中，已知曲线（为参数），以平面直角坐标系 的原点为极点，轴的正半轴为极轴，取相同的单位长度建立极坐标系，已知直线.‎ ‎（1）将曲线上的所有点的横坐标、纵坐标分别伸长为原来的，2倍后得到曲线，试写出直线的直角坐标方程和曲线的参数方程；‎ ‎（2）求曲线C上的点到直线的最大距离.‎