2018届二轮复习第8节函数图象与零点课件（全国通用） 23页

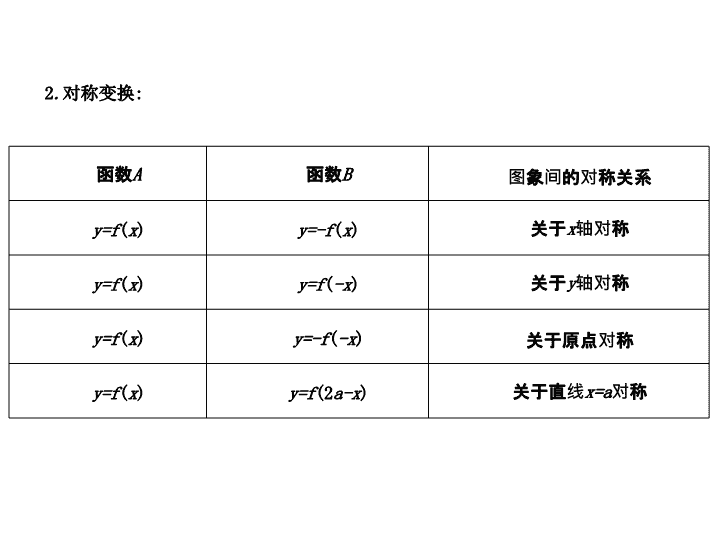
第三章　函 数 第 8 节 函数图象与零点 1 . 平移变换 : 原函数 图象变换 ( a> 0) 变换后的函数 y=f ( x ) 向左平移 a 个单位 y=f ( x+a ) y=f ( x ) 向右平移 a 个单位 y=f ( x-a ) y=f ( x ) 向上平移 a 个单位 y=f ( x ) +a y=f ( x ) 向下平移 a 个单位 y=f ( x ) -a 2 . 对称变换 : 函数 A 函数 B 图象间的对称关系 y=f ( x ) y=-f ( x ) 关于 x 轴对称 y=f ( x ) y=f ( -x ) 关于 y 轴对称 y=f ( x ) y=-f ( -x ) 关于原点对称 y=f ( x ) y=f (2 a-x ) 关于直线 x=a 对称 3 . 翻折变换 : 原函数 图象变换过程 变换后的函数 y=f ( x ) 作 y=f ( x ) 的图象 , 将图象位于 x 轴下方的部分以 x 轴为对称轴翻折到 x 轴上方 , 其余部分不变 . y= | f ( x )| y=f ( x ) 作 y=f ( x ) 在 y 轴上及 y 轴右边的图象部分 , 并作 y 轴右边的图象关于 y 轴对称的图象 . y=f (| x |) 4 . 具有对称性的抽象函数 : 函数 f ( x ) 对于定义域中的任意 x , 都有 (1) f ( a + x ) =f ( b-x ), 则 f ( x ) 关于直线 x = 对称 ; (2) f ( a + x )= -f ( b-x ), 则 f ( x ) 关于点 ( ,0) 对称 . 5 . 函数的零点 : 使得函数 f ( x ) = 0 时的 x 的值叫函数的零点 . 判断方法 : 若函数 f ( x ) = 0 在 [ a , b ] 上连续 , 当 f ( a )· f ( b )<0 时 , f ( x ) 在 [ a , b ] 上至少有一个零点 . 【 例 1】 (2013 青岛一模 ) 函数 y= 2 1 -x 的大致图象为 ( ) A.0 B.1 C.2 D.3 2 . 函数 f ( x ) = | x- 2| - ln x 在定义域内的零点个数为 ( ) A.0 B.1 C.2 D.3 【答案】C 【解析】 f ( x ) = | x- 2| - ln x= 0时,| x- 2| = ln x ,分别画出 y= | x- 2|和 y= ln x 的图象,可以看出它们有2个交点,所以 f ( x ) = | x- 2| - ln x 在定义域内的零点个数为2个,选C . 3 . (2014 全国新课标 (Ⅱ)) 已知偶函数 f ( x ) 的图象关于直线 x =2 对称 , 且 f (3) = 3, 则 f ( - 1)= . 【 答案 】3 【 解析 】 因为 f ( x ) 的图象关于直线 x= 2 对称 , 所以有 f (3) =f (1) = 3, 又因为 f ( x ) 为偶函数 , 所以 f ( - 1) = 3 . 5 . (2011 陕西高考文科 ) 方程 | x |=cos x 在 ( - ∞,+∞) 内 ( ) A. 没有根 B. 有且仅有一个根 C. 有且仅有两个根 D. 有无穷多个根 【答案】 C 【解析】 分别画出 y= | x |和 y= cos x 的图象,可以看出它们有2个交点,选C . 6 . 根据表格中的数据 , 可以判断方程 e x -x- 2 = 0 必有一个根在区间 ( ) A.( - 1,0) B.(0,1) C.(1,2) D.(2,3) 【 答案 】C 【 解析 】 当 x= 0 时 , e x - ( x +2) =e 0 - (0 + 2) = 1 - 2 = ( - 1)<0, 当 x= 1 时 , e x - ( x +2) =e 1 - (1+2) =e- 3<0, 当 x= 2 时 , e x - ( x +2) =e 2 - (2+2)=7 . 39 - 4>0, 所以 e x -x- 2 = 0 必有一个根在区间 (1,2) 上 , 选 C . x - 1 0 1 2 3 e x 0 . 37 1 2 . 78 7 . 39 20 . 09 x +2 1 2 3 4 5 7 . 函数 f ( x )=( x-a )( x-b )( 其中 a > b ) 的图象如下图所示 , 则函数 g ( x )= a x + b 的图象是 ( ) 【 答案 】A 【 解析 】 由函数 f ( x )=( x-a )( x-b )( 其中 a>b ) 的图象知道 , f ( x )=0 时 , x 1 = b < - 1, x 2 = a , 其中 0< a <1, 所以对应的 y=a x 图象应该是单调递减函数 , 而 b < - 1, 所以 , g ( x )= a x + b 应该是由 y = a x 向下平移 | b | 个单位得到 . 因为 b < - 1 . 选 A . 8 . (2013 全国新课标 (Ⅱ)) 若存在正数 x 使 2 x ( x-a )<1 成立 , 则 a 的取值范围是 ( ) A.(-∞,+∞) B.(-2,+∞) C.(0,+∞) D.(-1,+∞) 【答案】 D 【解析】 因为2 x >0,所以由2 x ( x-a )<1得 x-a < =2 -x ,在坐标系中,作出函数 f ( x )= x-a , g ( x )=2 -x 的图象,当 x >0时, g ( x )=2 -x <1,所以如果存在 x >0,使2 x ( x-a )<1,则有 -a <1,即 a > - 1,所以选D . 9 . (2013 福建高考文科 ) 函数 f ( x ) = ln( x 2 +1) 的图象大致是 ( ) 【 答案 】 A 【 解析 】 f ( x ) = ln( x 2 +1) 是偶函数 , 图象关于 y 轴对称 , 排除 C . 当 x =0 时 , f (0)=ln(0+1)=ln1 = 0, 排除 B 、 D, 所以选 A . 【 答案 】 D 【 解析 】 当 x =1 时 , f (1) = 1+1+sin1>2, 排除 A 、 C; 当 x →+∞ 时 , y →1+ x , 排除 B, 故选 D. 12 . 函数 f ( x ) = |2 x - 2| -b 有两个零点 , 则实数 b 的取值范围是 . 【答案】(0,2) 【解析】 由函数 f ( x ) = |2 x - 2| -b 有两个零点,可得|2 x - 2|= b 有两个不等的根,从而可得函数 y =|2 x - 2|函数 y = b 的图象有两个交点,结合函数的图象可得,0< b <2,故答案为:(0,2) . 13 . 如图 , 函数 f ( x ) 的图象为折线 ACB , 则不等式 f ( x )≥log 2 ( x +1) 的解集是 ( ) A.{ x | - 1