- 1.34 MB
- 2021-04-27 发布
青阳一中 2019-2020 学年度 9 月份月考试卷
高二数学
命题人:
第Ⅰ卷
一、选择题:本大题共 12 小题,每小题 5 分,在每小题给出的四个选项中,只有一项是符合
题目要求的。
1.已知全集 U={1,2,3, 4,5,6,7,8},集合 A={2,3,5,6},集合 B={1,3,4,6,7},则集合
A∩(∁UB)等于( )
A.{2,5} B.{3,6} C.{2,5,6} D.{2,3,5,6,8}
2. 有 10 名工人某天生产同一种零件,生产的件数分别为 15,17,14,10,15,17,17,16,
14,12,设其平均数为 a,中位数为b ,众数为 c ,则有( )
A. cba B. acb C. bac D. abc
3.在等差数列 }{ na 中, 3 4 2 2a a a ,则数列 }{ na 的前 9 项之和 9S 等( )
A.63 B.45 C. 36 D.18
4.函数 y=3sin 的图象可看成 y=3sin3x 的图象( )
A.向左平移 个单位长度得到 B.向右平移 个单位长度得到
C.向左平移 个单位长度得到 D.向右平移 个单位长度得到
5.如图,正方形 BCDE 和 ABFG 的边长分别为 2a , a ,连接 CE 和 CG ,在两个正方形区域
内任取一点,则该点位于阴影部分的概率是( )
A. 3
5 B. 3
8 C. 3
10 D. 3
20
6.右图是水平放置的某个三角形的直观图,D′是△A′B′C′中 B′C′边的中点且 A′D′
∥y′轴,A′B′,A′D′,A′C′三条线段对应原图形中的线段 AB,AD,AC,那么( )
A.最长的是 AB,最短的是 AC B.最长的是 AC,最短的是 AB
C.最长的是 AB,最短的是 AD D.最长的是 AD,最短的是 AC
7.设 f(x)=
x+1,x>0,
1-x,x=0,
-1,x<0,
则 f(f(0))等于( )
A.1 B.0 C.2 D.-1
8.某几何体的三视图如图所示,则其体积为( )
A. 4 B.8
C.12 D. 24
9. 如果实数 x , y 满足约束条件
1 0,
1 0,
1 0,
x y
y
x y
则 2x y 的最大值为( )
A. 3 B. 2 C. 1 D. 2
10.在 ABC△ 中, sin 3 2 sinB A , 2BC ,且 π
4C ,则 AB ( )
A. 26 B.5 C. 3 3 D. 2 6
11.已知 f x 是定义在 R 上的奇函数,当 0x 时, 22xf x x ,则不等式 2 1 3f x 的
解集为( )
A. 1, B. 2, C. 2 2 , D. 1 2 ,
12.若正数 x,y 满足 x2+3xy-1=0,则 x+y 的最小值是( )
A. 2
3 B.2 2
3 C. 3
3 D.2 3
3
第Ⅱ卷
二、填空题:本大题共 4 小题,每小题 5 分。
13.已知向量 a 与 b 的夹角为 60 , 2a , 3b ,则 3 2 a b __________.
14.已知 ��,5
4cos,2
3,
,则 )4tan( =
15.已知数列{an}满足:a1=m(m 为正整数),an+1=
an
2
当 an 为偶数时 ,
3an+1 当 an 为奇数时 .
若 a3=1,则 m 所有可能的取值为________.
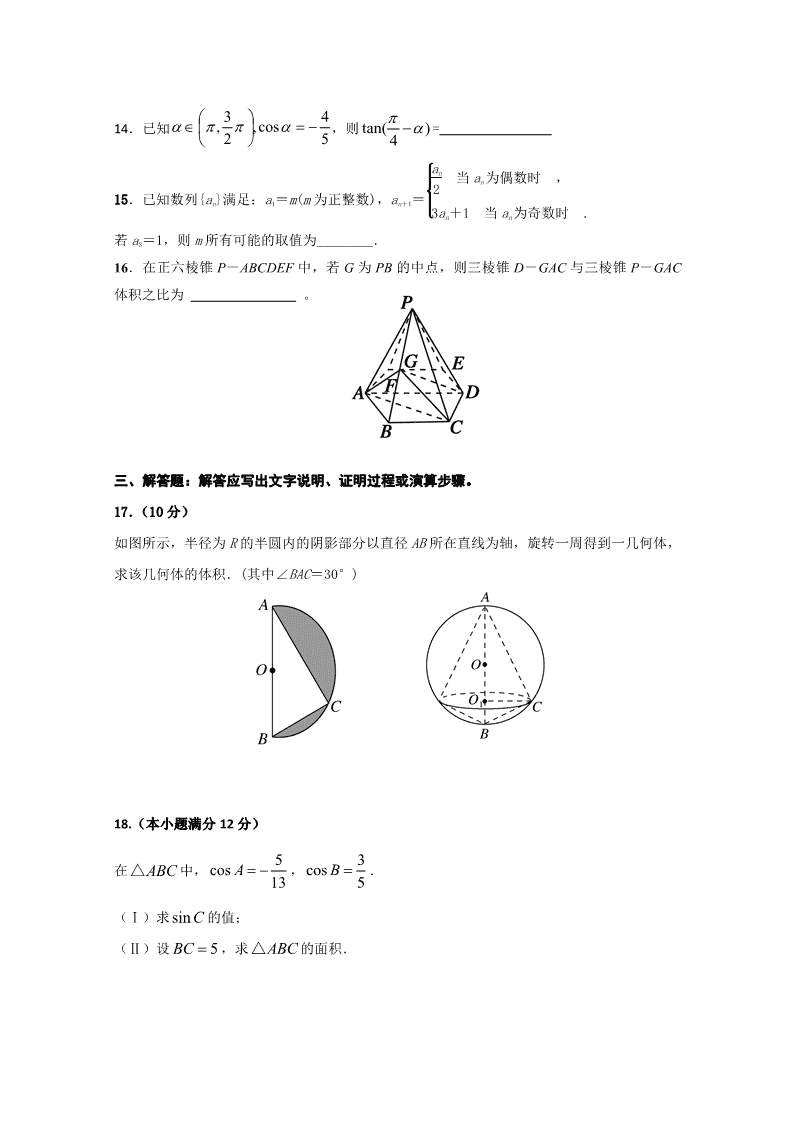
16.在正六棱锥 P-ABCDEF 中,若 G 为 PB 的中点,则三棱锥 D-GAC 与三棱锥 P-GAC
体积之比为 。
三、解答题:解答应写出文字说明、证明过程或演算步骤。
17.(10 分)
如图所示,半径为 R 的半圆内的阴影部分以直径 AB 所在直线为轴,旋转一周得到一几何体,
求该几何体的体积.(其中∠BAC=30°)
18.(本小题满分 12 分)
在 ABC△ 中, 5cos 13A , 3cos 5B .
(Ⅰ)求sinC 的值;
(Ⅱ)设 5BC ,求 ABC△ 的面积.
19.(12 分)
某地区 2011年至 2017 年农村居民家庭人均纯收入 y (单位:千元)的数据如下表:
(1)若 y 关于 t 的线性回归方程为 2 3y bt .,根据图中数据求出实数 b 并预测 2018 年该地
区农村居民家庭人均纯收入;
(2)在 2011年至 2017 年中随机选取两年,求这两年人均纯收入都高于3 6.千元的概率.
20. (12 分)
已知函数 f(x)=sin ωx-cos ωx(ω>0)的最小正周期为π.
(1)求函数 y=f(x)图象的对称轴方程;
(2)讨论函数 f(x)在
0,π
2 上的单调性
21、(12 分)
已知{an}是等差数列,{bn}是等比数列,且 b2=3,b3=9,a1=b1,a14=b4.
(1)求{an}的通项公式;
(2)设 cn=an+bn,求数列{cn}的前 n 项和.
22.(12 分)
已知函数 .
(1)解不等式 ;
(2)若 时, 恒成立,求 的取值范围.
数学答案
1 答案 A【解析】根据补集的定义可得∁UB={2,5,8},所以 A∩(∁UB)={2,5},故选 A.
2 答案 D
3 答案 D【解析】 , 。
4【答案】A.【解析】因为 y=3sin =3sin3(x+ ),所以 y=3sin3x 的图象向左
平移 个单位长度得 y=3sin 的图象.
5【答案】C【解析】设 ,由 ,得 ,即 ,
则 , ,
由几何概型的概率公式,得 .故选 C.
6 答案 C【解析】A′D′∥y′轴,根据斜二测画法规则,在原图形中应有 AD⊥BC,又 AD 为
BC 边上的中线,所以△ABC 为等腰三角形.AD 为 BC 边上的高,则有 AB,AC 相等且最长,AD
最短.
7 答案 C【解析】 f(0)=1-0=1,f(f(0))=f(1)=1+1=2.
8 【 答 案 】 A 【 解 析 】 由 三 视 图 可 知 : 该 几 何 体 为 四 棱 锥 , 由 体 积 公 式 易 得
.
故选 A.
9 答案 C
10【答案】A【解析】由正弦定理知 ,又 知, ,所以由余弦定理
知: ,所以 ,故选 A.
11【答案】A【解析】由于 是定义在 上的奇函数,∴ ,且在 上
为增函数,
∴ 是 上的增函数,∵ ,所以 ,∴ ,∴ .故
选 A.
12 答案 B 解析 对于 x2+3xy-1=0 可得 y=
1
3
1
-x,∴x+y=
2x
3 +
1
3x≥2
2
9=
2
3(当且仅当 x=
2
2时
等号成立).故选 B.
13 【 答 案 】 【 解 析 】 , , 与 的 夹 角 为 ,
,
又 , ,故答案为 .
14【答案】 【解析】因 ,所以 ,
15[答案] 4 解析:(1)若 a1=m 为偶数,a2=m
2 ,①当m
2 为偶数时,a3=m
4 ,故m
4 =1⇒m
=4;②当m
2 为奇数时,a3=3m
2 +1,由3m
2 +1=1 得 m=0(舍去).(2)若 a1=m 为奇数,则 a2
=3a1+1=3m+1 为偶数,故 a3=3m+1
2 必为偶数,所以3m+1
2 =1 可得 m=1
3(舍去).
16 [答案] 2:1[解析] 设棱锥的高为 h,VD-GAC=VG-DAC=
1
3S△ADC·
1
2h,VP-GAC=
1
2VP-ABC=VG-ABC
=
1
3S△ABC·
h
2.又 S△ADC
S△ABC=2:1,故 VD-GAC
VP-GAC=2:1.
17 解 如图所示,过 C 作 CO1⊥AB 于 O1.在半圆中可得∠BCA=90°,
∠BAC=30°,AB=2R,∴AC=R,CO1=
3
2R,
∴V 圆锥 AO1+V 圆锥 BO1=1
3π·CO
2
1·AO1+1
3π·CO
2
1·BO1=1
3π·CO
2
1·(AO1+BO1)
=1
3π×3
R×2R=π
2R3,又 V 球=4
3πR3,∴所求几何体的体积 V=4
3πR3-π
2R3=5
6πR3.
……………………(10 分)
18 (Ⅰ)由 ,得 ,由 ,得 .
所以 .……………………(6 分)
(Ⅱ)由正弦定理得 .
所以 的面积 .…………(12 分)
19【答案】(1) , 年该地区农村居民家庭人均纯收入为 千元;(2) .
【 解 析 】 ( 1 ) 由 题 , ,
,
代入得, ,当 时, (千元)……………………(6 分)
( 2 ) 记 :
,即 ,记事件 “这两年人均纯收入都高于 千
元”,
则 , 即 , 则
.……………………(12 分)
20 【解析】(1)∵f(x)=sin ωx-cos ωx=sin
π
4 ,且 T=π,∴ω=2,于是 f(x)=sin
π
4 .
令 2x-
π
4 =kπ+
π
2 (k∈Z),得 x=
kπ
2 +
3π
8 (k∈Z).
即函数 f(x)图象的对称轴方程为 x=
kπ
2 +
3π
8 (k∈Z). ……………………(6 分)
(2)令 2kπ-
π
2 ≤2x-
π
4 ≤2kπ+
π
2 (k∈Z),
得函数 f(x)的单调递增区间为
3π
8 (k∈Z).
∵x∈
π
2 ,∴令 k=0,
得函数 f(x)在
π
2 上的单调递增区间为
3π
8 ;
同理,其单调递减区间为
π
2 .……………………(12 分)
21 [解析] (1)等比数列{bn}的公比 q=
b3
b2=
9
3=3,所以 b1=
b2
q =1,b4=b3q=27.设等差数列
{an}的公差为 d.
因为 a1=b1=1,a14=b4=27,所以 1+13d=27,即 d=2.所以 an=2n-1(n=1,2,3,…).
……………………(6 分)
(2)由(1)知,an=2n-1,bn=3n-1,因此 cn=an+bn=2n-1+3n-1.从而数列{cn}的前 n 项和
Sn=1+3+…+(2n-1)+1+3+…+3n-1=
n(1+2n-1)
2 +
1-3n
1-3 =n2+
3n-1
2 .
……………………(12 分)
22 【详解】
(1)由 可得 即
当 时,不等式解集为 ;
当 时,不等式解集为 ;
当 时,不等式解集为 .
……………………(6 分)
(2) 即 对 恒成立,
令 ,等价于 对 恒成立,
又 ,当且仅当 即 时等号成立
的取值范围为 ……………………(12 分)