高考文科数学专题复习练习3二元一次不等式(组)表示的平面区域问题 8页

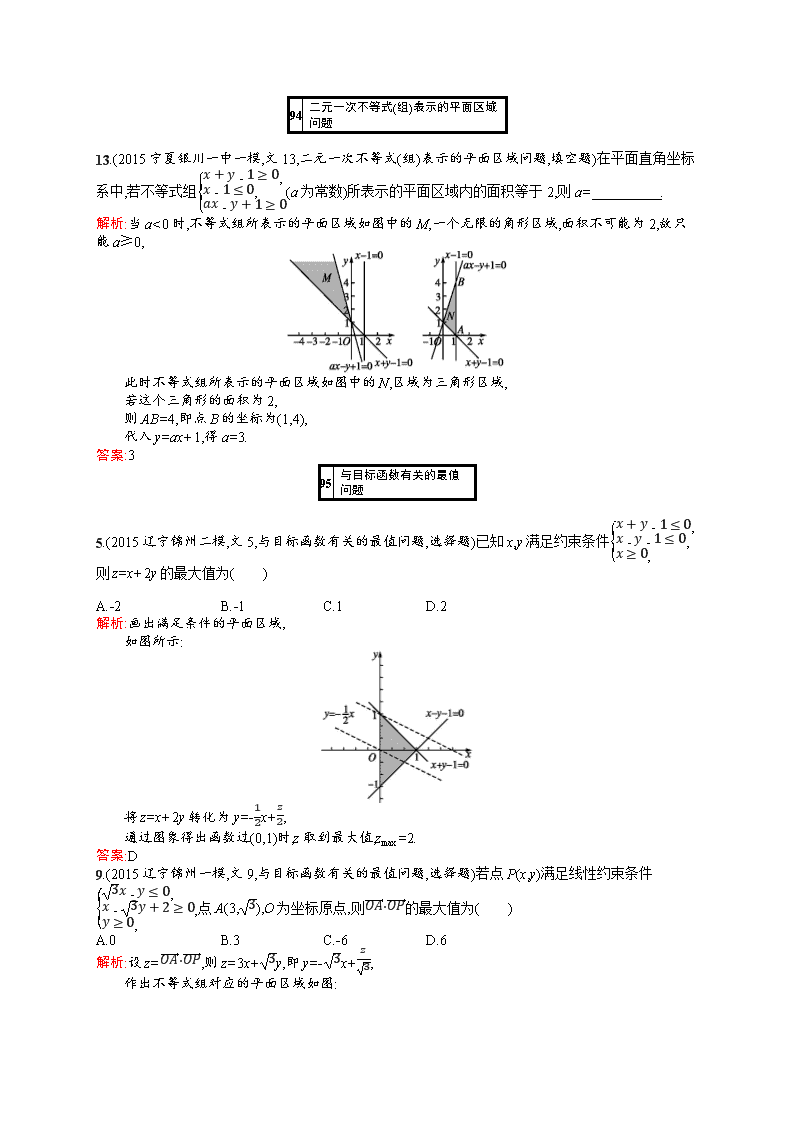
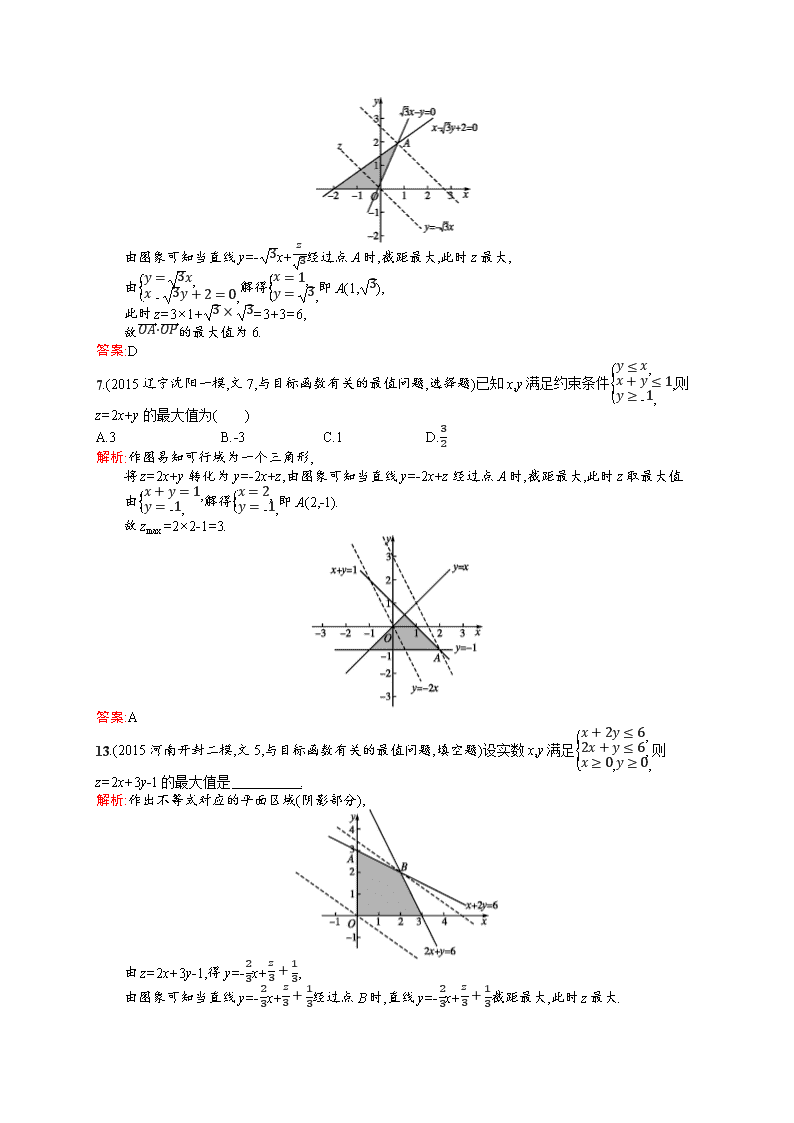
‎94‎ 二元一次不等式(组)表示的平面区域问题 ‎13.(2015宁夏银川一中一模,文13,二元一次不等式(组)表示的平面区域问题,填空题)在平面直角坐标系中,若不等式组x+y-1≥0,‎x-1≤0,‎ax-y+1≥0‎(a为常数)所表示的平面区域内的面积等于2,则a=　　　　　. ‎ 解析:当a<0时,不等式组所表示的平面区域如图中的M,一个无限的角形区域,面积不可能为2,故只能a≥0,‎ 此时不等式组所表示的平面区域如图中的N,区域为三角形区域,‎ 若这个三角形的面积为2,‎ 则AB=4,即点B的坐标为(1,4),‎ 代入y=ax+1,得a=3.‎ 答案:3‎ ‎95‎ 与目标函数有关的最值问题 ‎5.(2015辽宁锦州二模,文5,与目标函数有关的最值问题,选择题)已知x,y满足约束条件x+y-1≤0,‎x-y-1≤0,‎x≥0,‎则z=x+2y的最大值为(　　)‎ ‎　　　　　　　　　　　　　　　　‎ A.-2 B.-1 C.1 D.2‎ 解析:画出满足条件的平面区域,‎ 如图所示:‎ 将z=x+2y转化为y=-‎1‎‎2‎x+z‎2‎,‎ 通过图象得出函数过(0,1)时,z取到最大值,zmax=2.‎ 答案:D ‎9.(2015辽宁锦州一模,文9,与目标函数有关的最值问题,选择题)若点P(x,y)满足线性约束条件‎3‎x-y≤0,‎x-‎3‎y+2≥0,‎y≥0,‎点A(3,‎3‎),O为坐标原点,则OA‎·‎OP的最大值为(　　)‎ A.0 B.3 C.-6 D.6‎ 解析:设z=OA‎·‎OP,则z=3x+‎3‎y,即y=-‎3‎x+z‎3‎,‎ 作出不等式组对应的平面区域如图:‎ 由图象可知当直线y=-‎3‎x+z‎3‎经过点A时,截距最大,此时z最大,‎ 由y=‎3‎x,‎x-‎3‎y+2=0,‎解得x=1,‎y=‎3‎,‎即A(1,‎3‎),‎ 此时z=3×1+‎3‎‎×‎‎3‎=3+3=6,‎ 故OA‎·‎OP的最大值为6.‎ 答案:D ‎7.(2015辽宁沈阳一模,文7,与目标函数有关的最值问题,选择题)已知x,y满足约束条件y≤x,‎x+y≤1,‎y≥-1,‎则z=2x+y的最大值为(　　)‎ A.3 B.-3 C.1 D.‎‎3‎‎2‎ 解析:作图易知可行域为一个三角形,‎ 将z=2x+y转化为y=-2x+z,由图象可知当直线y=-2x+z经过点A时,截距最大,此时z取最大值.‎ 由x+y=1,‎y=-1,‎解得x=2,‎y=-1,‎即A(2,-1).‎ 故zmax=2×2-1=3.‎ 答案:A ‎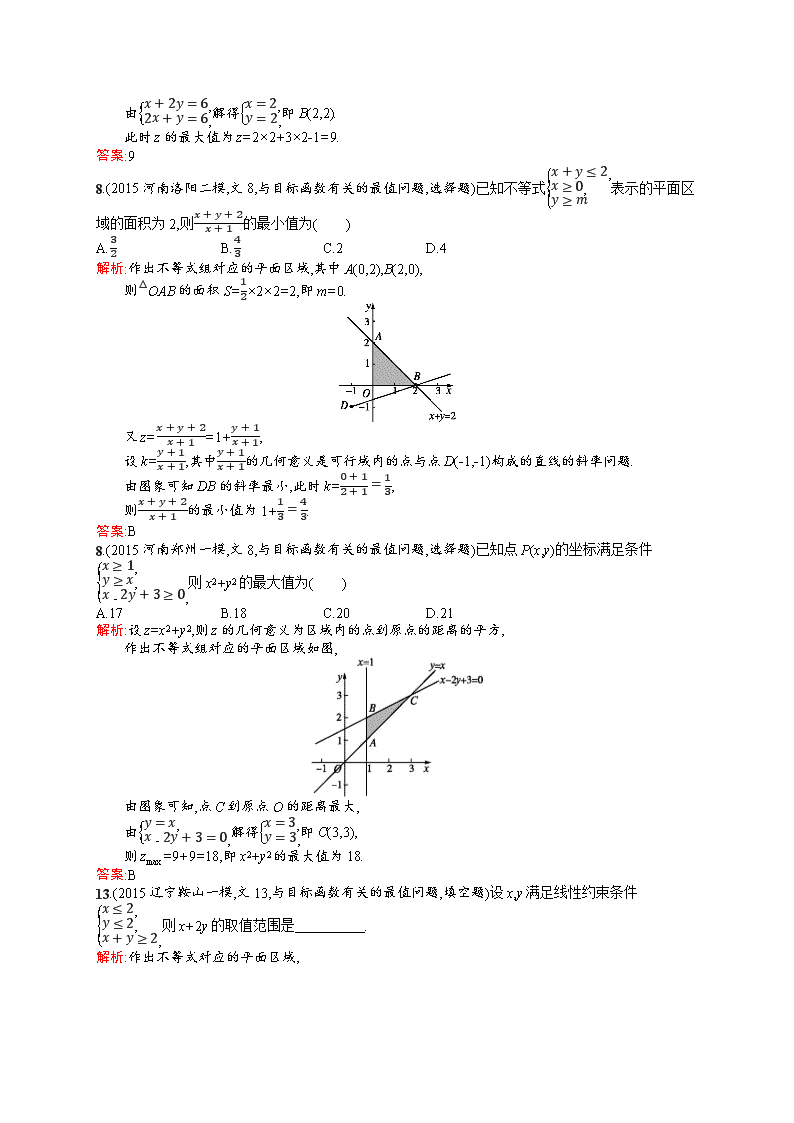13.(2015河南开封二模,文5,与目标函数有关的最值问题,填空题)设实数x,y满足x+2y≤6,‎‎2x+y≤6,‎x≥0,y≥0,‎则z=2x+3y-1的最大值是　　　　　. ‎ 解析:作出不等式对应的平面区域(阴影部分),‎ 由z=2x+3y-1,得y=-‎2‎‎3‎x+z‎3‎‎+‎‎1‎‎3‎,‎ 由图象可知当直线y=-‎2‎‎3‎x+z‎3‎‎+‎‎1‎‎3‎经过点B时,直线y=-‎2‎‎3‎x+z‎3‎‎+‎‎1‎‎3‎截距最大,此时z最大.‎ 由x+2y=6,‎‎2x+y=6,‎解得x=2,‎y=2,‎即B(2,2).‎ 此时z的最大值为z=2×2+3×2-1=9.‎ 答案:9‎ ‎8.(2015河南洛阳二模,文8,与目标函数有关的最值问题,选择题)已知不等式x+y≤2,‎x≥0,‎y≥m表示的平面区域的面积为2,则x+y+2‎x+1‎的最小值为(　　)‎ A.‎3‎‎2‎ B.‎4‎‎3‎ C.2 D.4‎ 解析:作出不等式组对应的平面区域,其中A(0,2),B(2,0),‎ 则△OAB的面积S=‎1‎‎2‎×2×2=2,即m=0.‎ 又z=x+y+2‎x+1‎=1+y+1‎x+1‎,‎ 设k=y+1‎x+1‎,其中y+1‎x+1‎的几何意义是可行域内的点与点D(-1,-1)构成的直线的斜率问题.‎ 由图象可知DB的斜率最小,此时k=‎0+1‎‎2+1‎‎=‎‎1‎‎3‎,‎ 则x+y+2‎x+1‎的最小值为1+‎1‎‎3‎‎=‎‎4‎‎3‎.‎ 答案:B ‎8.(2015河南郑州一模,文8,与目标函数有关的最值问题,选择题)已知点P(x,y)的坐标满足条件x≥1,‎y≥x,‎x-2y+3≥0,‎则x2+y2的最大值为(　　)‎ A.17 B.18 C.20 D.21‎ 解析:设z=x2+y2,则z的几何意义为区域内的点到原点的距离的平方,‎ 作出不等式组对应的平面区域如图,‎ 由图象可知,点C到原点O的距离最大,‎ 由y=x,‎x-2y+3=0,‎解得x=3,‎y=3,‎即C(3,3),‎ 则zmax=9+9=18,即x2+y2的最大值为18.‎ 答案:B ‎13.(2015辽宁鞍山一模,文13,与目标函数有关的最值问题,填空题)设x,y满足线性约束条件x≤2,‎y≤2,‎x+y≥2,‎则x+2y的取值范围是　　　　　. ‎ 解析:作出不等式对应的平面区域,‎ 由z=x+2y,得y=-‎1‎‎2‎x+z‎2‎,‎ 由图象可知当直线y=-‎1‎‎2‎x+z‎2‎经过点B(2,2)时,直线y=-‎1‎‎2‎x+z‎2‎的截距最大,此时z最大.‎ 此时z的最大值为z=2+2×2=6.‎ 当直线y=-‎1‎‎2‎x+z‎2‎经过点C(2,0)时,直线y=2的截距最小,此时z最小.‎ 此时z的最小值为z=2.‎ 故x+2y的取值范围是[2,6].‎ 答案:[2,6]‎ ‎9.(2015辽宁大连一模,文9,与目标函数有关的最值问题,选择题)在平面直角坐标系中,若P(x,y)满足x-4y+4≤0,‎‎2x+y-10≤0,‎‎5x-2y+2≥0,‎则x+2y的最大值是(　　)‎ A.2 B.8 C.14 D.16‎ 解析:作出不等式对应的平面区域,‎ 由z=x+2y,得y=-‎1‎‎2‎x+z‎2‎,‎ 由图象可知当直线y=-‎1‎‎2‎x+z‎2‎经过点A时,截距最大,此时z最大.‎ 由x-4y+4=0,‎‎2x+y-10=0,‎得x=4,‎y=2,‎ 即A(4,2),此时z的最大值为z=4+2×2=8.‎ 答案:B ‎7.(2015宁夏银川一中二模,文7,与目标函数有关的最值问题,选择题)已知点M(x,y)的坐标满足x-y+5≥0,‎x+y≥0,‎x≤3,‎N点的坐标为(1,-3),点O为坐标原点,则ON‎·‎OM的最小值是(　　)‎ A.12 B.5 C.-6 D.-21‎ 解析:设z=ON‎·‎OM=x-3y,‎ 由z=x-3y,得y=‎1‎‎3‎x-z‎3‎,‎ 作出不等式组对应的平面区域如图(阴影部分):‎ 由图象可知当直线y=‎1‎‎3‎x-z‎3‎经过点A时,直线y=‎1‎‎3‎x-z‎3‎的截距最大,‎ 此时z最小,由x=3,‎x-y+5=0,‎ 解得x=3,‎y=8,‎即A(3,8),‎ 此时代入目标函数z=x-3y,得z=3-3×8=-21.‎ 故ON‎·‎OM的最小值是-21.‎ 答案:D ‎7.(2015河南六市联考一模,文7,与目标函数有关的最值问题,选择题)已知正数x,y满足‎2x-y≤0,‎x-3y+5≥0,‎则z=4-x·‎1‎‎2‎y的最小值为(　　)‎ A.1 B.‎1‎‎4‎‎3‎‎2‎ C.‎1‎‎16‎ D.‎‎1‎‎32‎ 解析:z=4-x·‎1‎‎2‎y=2-2x·2-y=2-2x-y,‎ 设m=-2x-y,要使z最小,则只需求m的最小值即可.‎ 作出不等式组对应的平面区域如图:‎ 由m=-2x-y,得y=-2x-m,由图象可知当直线y=-2x-m经过点B时,直线y=-2x-m的截距最大,此时m最小.‎ 由‎2x-y=0,‎x-3y+5=0,‎ 解得x=1,‎y=2,‎即B(1,2),‎ 此时m=-2-2=-4,‎ 故z=4-x·‎1‎‎2‎y的最小值为2-4=‎1‎‎16‎.‎ 答案:C ‎9.(2015河南开封定位模拟,文9,与目标函数有关的最值问题,选择题)设变量x,y满足约束条件x-y≤1,‎x+y≥2,‎y≤2,‎则目标函数z=x2+y2的取值范围为(　　)‎ A.[2,8] B.[4,13] C.[2,13] D.‎‎5‎‎2‎‎,13‎ 解析:作出不等式对应的平面区域,‎ 则z=x2+y2的几何意义为平面区域内动点P(x,y)到原点的距离的平方,‎ 则当动点P位于A时,点A到原点O的距离最大,‎ 当直线x+y=2与圆x2+y2=z相切时,距离最小,‎ 即原点到直线x+y=2的距离d=‎2‎‎1+1‎‎=‎2‎‎2‎=‎‎2‎,即z的最小值为z=d2=2,‎ 由y=2,‎x-y=1,‎解得x=3,‎y=2,‎ 即A(3,2),‎ 此时z=x2+y2=32+22=9+4=13,‎ 即z的最大值为13.故z=x2+y2的取值范围为[2,13].‎ 答案:C ‎3.(2015河南商丘二模,文3,与目标函数有关的最值问题,选择题)已知变量x,y满足约束条件x+2y≥1,‎x-y≤1,‎y-1≤0,‎则z=x-2y的最大值为(　　)‎ A.-3 B.0 C.1 D.3‎ 解析:作出不等式组x+2y≥1,‎x-y≤1,‎y-1≤0‎表示的平面区域,‎ 得到如图的△ABC及其内部,其中A(-1,1),B(2,1),C(1,0).‎ 设z=x-2y,即y=‎1‎‎2‎x-‎1‎‎2‎z,当直线y=‎1‎‎2‎x-‎1‎‎2‎z经过点C时,目标函数z达到最大值,‎ 故z最大值=1.‎ 答案:C ‎13.(2015河南商丘一模,文13,与目标函数有关的最值问题,填空题)若x,y满足不等式组x-2y+4≤0,‎x-6y+28≥0,‎x≥2,‎则yx的最小值为　　　　　. ‎ 解析:由约束条件x-2y+4≤0,‎x-6y+28≥0,‎x≥2‎作可行域如图,‎ 联立x-6y+28=0,‎x-2y+4=0,‎解得A(8,6),yx的几何意义为可行域内的动点与原点连线的斜率,‎ 由图可知,当动点为A(8,6)时,kOA最小为‎6‎‎8‎‎=‎‎3‎‎4‎.‎ 答案:‎‎3‎‎4‎ ‎6.(2015河南中原名校联盟模拟,文6,与目标函数有关的最值问题,选择题)设x,y满足约束条件x-y+2≥0,‎x≤2,‎y≥1,‎则z=x+2y的最小值是(　　)‎ A.0 B.1 C.4 D.8‎ 解析:由约束条件x-y+2≥0,‎x≤2,‎y≥1‎作出可行域如图,‎ 由z=x+2y,得y=-‎1‎‎2‎x+z‎2‎,‎ 由图可知,当直线y=-‎1‎‎2‎x+z‎2‎过点A(-1,1)时,目标函数取得最小值为-1+2×1=1.‎ 答案:B ‎97‎ 利用基本不等式求最值 ‎14.(2015辽宁锦州二模,文14,利用基本不等式求最值,填空题)已知x>0,y>0,且x+y=‎3‎‎4‎,则‎4‎x‎+‎‎1‎y的最小值为　　　　　. ‎ 解析:∵x>0,y>0,且x+y=‎3‎‎4‎,‎ ‎∴‎4‎x‎+‎1‎y=‎‎4‎‎3‎(x+y)‎‎4‎x‎+‎‎1‎y ‎=‎4‎‎3‎‎5+‎4yx+‎xy‎≥‎‎4‎‎3‎‎5+2‎‎4yx‎·‎xy=12,‎ 当且仅当x=2y=‎1‎‎2‎时取等号.‎ 因此‎4‎x‎+‎‎1‎y的最小值为12.‎ 答案:12‎ ‎13.(2015辽宁沈阳四校联考,文13,利用基本不等式求最值,填空题)设x,y满足约束条件‎3x-y-6≤0,‎x-y+2≥0,‎x≥0,y≥0,‎若目标函数z=ax+by(a>0,b>0)的最大值为6,则‎1‎a‎+‎‎2‎b的最小值为　　　　　. ‎ 解析:作出不等式组对应的平面区域如图:‎ 由z=ax+by(a>0,b>0),得y=-abx+zb,‎ 则直线的斜率k=-ba<0,截距最大时,z也最大.‎ 由图象可知当直线y=-abx+zb经过点A时,‎ 直线y=-abx+zb的截距最大,此时z最大,‎ 由‎3x-y-6=0,‎x-y+2=0,‎解得x=4,‎y=6,‎ 即A(4,6),此时z=4a+6b=6,即‎2a‎3‎+b=1,‎ ‎∴‎‎1‎a‎+‎2‎b=‎1‎a‎+‎‎2‎b‎2a‎3‎‎+b=‎8‎‎3‎+ba+‎‎4a‎3‎ ‎≥‎8‎‎3‎+2ba‎·‎‎4a‎3‎‎=‎8‎‎3‎+‎4‎‎3‎‎3‎=‎‎8+4‎‎3‎‎3‎.‎ 当且仅当ba‎=‎‎4a‎3b,即a=‎3‎‎2‎b时取等号,即b=‎3-‎‎3‎‎2‎,a=‎3‎3‎-3‎‎4‎时取等号.‎ 答案:‎‎8+4‎‎3‎‎3‎ ‎6.(2015辽宁重点中学协作体模拟,文6,利用基本不等式求最值,选择题)若对任意正数x,不等式‎1‎x‎2‎‎+1‎‎≤‎ax恒成立,则实数a的最小值为(　　)‎ A.1 B.‎2‎ C.‎1‎‎2‎ D.‎‎2‎‎2‎ 解析:由题意可得a≥xx‎2‎‎+1‎恒成立.‎ 由于xx‎2‎‎+1‎‎=‎1‎x+‎‎1‎x≤‎‎1‎‎2‎(当且仅当x=1时,取等号),即xx‎2‎‎+1‎的最大值为‎1‎‎2‎,‎ 所以a≥‎1‎‎2‎,即a的最小值为‎1‎‎2‎.‎ 答案:C