- 234.00 KB
- 2021-04-27 发布
2018-2019学年山东省夏津一中高二第一次月考数学试题
一.选择题(共13小题,1-10为单选题,11-13为多选题,共52分)
1.给出下列命题中正确的是( )
A.棱柱被平面分成的两部分可以都是棱柱
B.底面是矩形的平行六面体是长方体
C.棱柱的底面一定是平行四边形
D.棱锥的底面一定是三角形
2.《九章算术》卷5《商功》记载一个问题“今有圆堡瑽,周四丈八尺,高一丈一尺.问积几何?答曰:二千一百一十二尺.术曰:周自相乘,以高乘之,十二而一”.这里所说的圆堡瑽就是圆柱体,它的体积为“周自相乘,以高乘之,十二而一”.就是说:圆堡瑽(圆柱体)的体积为(底面圆的周长的平方×高),则由此可推得圆周率π的取值为( )
A.3 B.3.1 C.3.14 D.3.2
3.如图,在正方体ABCD﹣A1B1C1D1中,M,N分别是BC1,CD1的中点,则下列说法错误的是( )
A.MN与CC1垂直 B.MN与AC垂直 C.MN与BD平行 D.MN与A1B1平行
4.已知一个圆柱的侧面展开图是边长为2π的正方形,则该圆柱的外接球表面积为( )
A. B.4π(π2+1) C. D.4π(π+1)
5.在直三棱柱ABC﹣A1BlC1中,平面α与棱AB,AC,A1C1,A1B1分别交于点E,F,G,H,且直线AA1∥平面α.有下列三个命题:①四边形EFGH是平行四边形;②平面α∥平面BCC1B1;③平面α⊥平面BCFE.其中正确的命题有( )
A.①② B.②③ C.①③ D.①②③
6.矩形ABCD中,AB=4,BC=3,沿AC将矩形ABCD折起,使面BAC⊥面DAC,则四面体A﹣BCD的外接球的体积为( )
A.π B.π C.π D.π
7.如图所示,Rt△A′B′C′为水平放置的△ABC的直观图,其中A′C′⊥B′C′,
B′O′=O′C′=1,则△ABC的面积为( )
A.2 B. C. D.
8.已知三棱锥S﹣ABC的四个顶点均在某个球面上,SC为该球的直径,△ABC是边长为4的等边三角形,三棱锥S﹣ABC的体积为,则此三棱锥的外接球的表面积为( )
A. B. C. D.
9.已知a,b,c表示不同的直线,α,β表示不同的平面,下列命题:
①若a∥b,b∥α,则a∥α;
②若a⊥b,b⊥α,c⊥α,则a⊥c;
③若a⊥b,b⊥α,则a∥α;
④若a∥b,b∥α,b⊂β,a∩β=c,则a∥c.
其中错误命题的序号是( )
A.①③ B.②④ C.③④ D.①②
10.如图1—2—87所示,四边形ABCD中,AD//BC,AD=AB,∠BCD=45°,∠BAD=90°,将△ABD沿BD折起,使平面ABD⊥平面BCD,构成四面体ABCD,则在四面体ABCD中,下列命题正确的是( )
A.平面ABD⊥平面ABC B.平面ADC⊥平面ABC
C.平面ADC⊥平面BDC D.平面ABC⊥平面BDC
11.在正方体ABCD﹣A1B1C1D1中,点P是线段BC1上任意一点,则下列结论中不正确的是( )
A.AD1⊥DP B.AP⊥B1C C.AC1⊥DP D.A1P⊥B1C
12.已知m,n是两条直线,α,β是两个平面.给出下列命题:A若m⊥α,m⊥n,则n∥α;B若m⊥β,n⊥β,则n∥m;C若m⊥α,m⊥β,则α∥β;D若α∥β,m⊂α,n⊂β,则n∥m;则正确的( )
13.对于不重合的两个平面α和β,给定下列条件:
A存在直线l,使得l⊥α,且l⊥β;
B存在平面γ,使得α⊥γ且β⊥γ;
Cα内有不共线的三点到β的距离相等;
D存在异面直线l,m,使得l∥α,l∥β,m∥α,m∥β
其中,可以判定α与β平行的条件有( )
二.填空题(共5小题,每小题4分,共20分)
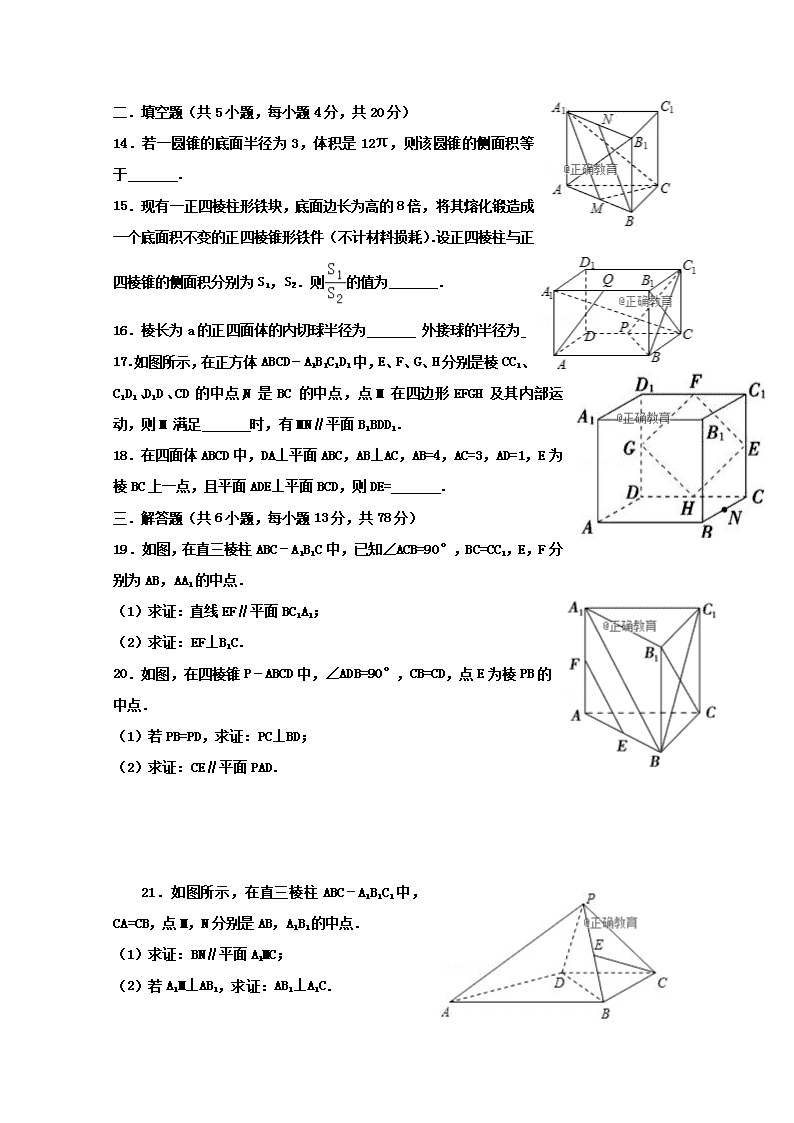
14.若一圆锥的底面半径为3,体积是12π,则该圆锥的侧面积等于 .
15.现有一正四棱柱形铁块,底面边长为高的8倍,将其熔化锻造成一个底面积不变的正四棱锥形铁件(不计材料损耗).设正四棱柱与正四棱锥的侧面积分别为S1,S2.则的值为 .
16.棱长为a的正四面体的内切球半径为 外接球的半径为
17.如图所示,在正方体ABCD﹣A1B1C1D1中,E、F、G、H分别是棱CC1、C1D1、D1D、CD的中点,N是BC的中点,点M在四边形EFGH及其内部运动,则M满足 时,有MN∥平面B1BDD1.
18.在四面体ABCD中,DA⊥平面ABC,AB⊥AC,AB=4,AC=3,AD=1,E为棱BC上一点,且平面ADE⊥平面BCD,则DE= .
三.解答题(共6小题,每小题13分,共78分)
19.如图,在直三棱柱ABC﹣A1B1C中,已知∠ACB=90°,BC=CC1,E,F分别为AB,AA1的中点.
(1)求证:直线EF∥平面BC1A1;
(2)求证:EF⊥B1C.
20.如图,在四棱锥P﹣ABCD中,∠ADB=90°,CB=CD,点E为棱PB的中点.
(1)若PB=PD,求证:PC⊥BD;
(2)求证:CE∥平面PAD.
21.如图所示,在直三棱柱ABC﹣A1B1C1中,CA=CB,点M,N分别是AB,A1B1的中点.
(1)求证:BN∥平面A1MC;
(2)若A1M⊥AB1,求证:AB1⊥A1C.
22.如图,四棱柱ABCD﹣A1B1C1D1为长方体,点P是CD中点,Q是A1B1的中点.
(I)求证:AQ∥平面PBC1;
(Ⅱ)若BC=CC1,求证:平面A1B1C⊥平面PBC1.
23.如图,在四棱锥P﹣ABCD中,底面ABCD为等腰梯形,AD∥BC,,E,F分别为线段AD,PB的中点.
(1)证明:PD∥平面CEF;
(2)若PE⊥平面ABCD,PE=AB=2,求四面体P﹣DEF的体积.
24.如图,正方体ABCD﹣A1B1C1D1的棱长为2,E,F分别是CB,CD的中点,点M在棱CC1上,CM=tCC1(0<t<1).
(Ⅰ)三棱锥C﹣EFM,C1﹣B1D1M的体积分别为V1,V2,当t为何值时,V1•V2最大?最大值为多少?
(Ⅱ)若A1C∥平面B1D1M,证明:平面EFM⊥平面B1D1M.
夏津一中高二上学期第一次月考数学试题答案
一.选择题(共13小题)
1AADBC.CADAB.
11.ACD 12.BC 13.AD
二.填空题(共5小题)
14.15π.15..16. 、 17.M在线段FH上18..
三.解答题(共6小题)
19.证明:(1)由题知,EF是△AA1B的中位线,
所以EF∥A1B……………(2分)
由于EF⊄平面BC1A1,A1B⊂平面BC1A1,
所以EF∥平面BC1A1.……………(6分)
(2)由题知,四边形BCC1B1是正方形,所以B1C⊥BC1.……(8分)
又∠A1C1B1=∠ACB=90°,所以A1C1⊥C1B1.
在直三棱柱ABC﹣A1B1C1中,CC1⊥平面A1C1B1,A1C1⊂平面A1C1B1,从而A1C1⊥CC1,
又CC1∩C1B1=C1,CC1,C1B1⊂平面BCC1B1,所以A1C1⊥平面BCC1B1,
又B1C⊂平面BCC1B1,所以A1C1⊥B1C..……………(10分)
因为A1C1∩BC1=C1,A1C1,BC1⊂平面BC1A1,所以B1C⊥平面BC1A1.……………(12分)
又A1B⊂平面BC1A1,所以B1C⊥A1B.
又由于EF∥A1B,所以EF⊥B1C.……………(13分)
20.证明:(1)取BD的中点O,连结CO,PO,
因为CD=CB,所以△CBD为等腰三角形,所以BD⊥CO.
因为PB=PD,所以△PBD为等腰三角形,所以BD⊥PO.
又PO∩CO=O,所以BD⊥平面PCO.
因为PC⊂平面PCO,所以PC⊥BD.
解:(2)由E为PB中点,连EO,则EO∥PD,
又EO⊄平面PAD,所以EO∥平面PAD.
由∠ADB=90°,以及BD⊥CO,所以CO∥AD,
又CO⊄平面PAD,所以CO∥平面PAD.
又CO∩EO=O,所以平面CEO∥平面PAD,
而CE⊂平面CEO,所以CE∥平面PAD.
21.证明:(1)因为ABC﹣A1B1C1是直三棱柱,所以AB∥A1B1,且AB=A1B1,
又点M,N分别是AB、A1B1的中点,所以MB=A1N,且MB∥A1N.
所以四边形A1NBM是平行四边形,从而A1M∥BN.
又BN⊄平面A1MC,A1M⊂平面A1MC,所以BN∥平面A1MC;
(2)因为ABC﹣A1B1C1是直三棱柱,所以AA1⊥底面ABC,而AA1⊂侧面ABB1A1,
所以侧面ABB1A1⊥底面ABC.
又CA=CB,且M是AB的中点,所以CM⊥AB.
则由侧面ABB1A1⊥底面ABC,侧面ABB1A1∩底面ABC=AB,
CM⊥AB,且CM⊂底面ABC,得CM⊥侧面ABB1A1.
又AB1⊂侧面ABB1A1,所以AB1⊥CM.
又AB1⊥A1M,A1M、MC平面A1MC,且A1M∩MC=M,
所以AB1⊥平面A1MC.
又A1C⊂平面A1MC,所以AB⊥A1C.
21.证明:(1)取AB中点为R,连接PR,B1R
∵点P是CD中点,Q是A1B1的中点,
∴四边形AQB1R,PRB1C1都为平行四边形,
∴AQ∥B1R,B1R∥PC1,∴AQ∥PC1.
∵AQ⊄平面PBC1,PC1⊂平面PBC1,
∴AQ∥平面PBC1.
(Ⅱ)∵四棱柱ABCD﹣A1B1C1D1为长方体,BC=CC1,
∴B1C⊥BC1.
∵A1B1⊥平面BB1C1C,∴A1B1⊥BC1.
∵A1B1∩B1C=B1,A1B1⊂平面A1B1C,B1C⊂平面A1B1C,
∴BC1⊥平面A1B1C,BC1⊂平面PBC1,
∴平面A1B1C⊥平面PBC1.
22.(1)证明:连接BE、BD,BD交CE于点O,
∵E为线段AD的中点,AD∥BC,,
∴BC∥ED,
∴四边形BCDE为平行四边形,
∴O为BD的中点,又F是BP的中点,
∴OF∥PD,
又OF⊂平面CEF,PD⊄平面CEF,
∴PD∥平面CEF;
(2)解:由(1)知,四边形BCDE为平行四边形,∴BE∥CD,
∵四边形ABCD为等腰梯形,AD∥BC,,
∴AB=AE=BE,
∴三角形ABE是等边三角形,
∴,
做BH⊥AD于H,则,
∵PE⊥平面ABCD,PE⊂平面PAD,
∴平面PAD⊥平面ABCD,
又平面PAD∩平面ABCD=AD,BH⊥AD,BH⊂平面ABCD,
∴BH⊥平面PAD,
∴点B到平面PAD的距离为,
又∵F为线段PB的中点,
∴点F到平面PAD的距离等于点B到平面PAD的距离的一半,即,又,
∴=.
23.解:(Ⅰ)由题可知,CM=2t,C1M=2﹣2t,
∴V1=S△ECF•CM==,
V2=S•C1M=(2﹣2t)=(1﹣t),
∴V1•V2=≤•()2=.
当且仅当t=1﹣t,即t=时等号成立.
所以当t=时,V1•V2最大,最大值为.
(Ⅱ)连接A1C1交B1D1于点O,则O为A1C1的中点,
∵A1C∥平面B1D1M,平面A1CC1∩平面B1D1M=OM,
∴A1C∥OM,∴M为CC1的中点,
连接BD,∵E,F为BC、CD的中点,
∴EF∥BD,又AC⊥BD,∴AC⊥EF.
∵AA1⊥平面ABCD,EF⊂平面ABCD,
∴AA1⊥EF,又AA1∩AC=A,
∴EF⊥平面A1AC,又A1C⊂平面A1AC,
∴EF⊥A1C.
同理可得:EM⊥A1C,又EF∩EM=E,
∴A1C⊥平面EFM.
又A1C∥平面B1D1M,
∴平面EFM⊥平面B1D1M.