- 469.50 KB
- 2021-04-27 发布
宜昌市葛洲坝中学2018-2019学年第一学期
高二年级期中考试试卷数学(理科)试题
考试时间:2018年11月
第Ⅰ卷
一、选择题(本题共12小题,每小题5分,共60分,在每小题给的四个选项中,只有一个是符合题目要求的)
1.设直线的倾斜角为,且,则满足( )
A. B. C. D.
2.用“辗转相除法”求得和的最大公约数是( )
A. B. C. D.
3.直线,当变动时,所有直线都通过定点( )
A. B. C. D.
4.圆关于原点对称的圆的方程为 ( )
A. B.
C. D.
5.有件产品编号从到,现在从中抽取件检验,用系统抽样确定所抽取的编号为( )
A.5,10,15,20,25 B.5,15,20,35,40 C.10,20,30,40,50 D.5,11,17,23,29
6.在一次歌手大奖赛上,七位评委为歌手打出的分数如下:
9.4 8.4 9.4 9.9 9.6 9.4 9.7
去掉一个最高分和一个最低分后,所剩数据的平均值和方差分别为 ( )
A. B. C. D.
7.圆在点处的切线方程为( )
A. B. C. D.
8.是指悬浮在空气中的空气动力学当量直径小于或 等于的颗粒物,也称为细颗粒物,一般情况下浓度(单位: )越大,大气环境质量越差.如图所示的是
宜昌市区甲、乙两个监测站某日内每日的浓度读数的茎叶图,则下列说法正确的是( )
A.这10日内甲、乙监测站读数的极差相等
B.这10日内甲、乙监测站读数的中位数中,乙的较大
C.这10日内乙监测站读数的众数与中位数相等
D.这10日内甲、乙监测站读数的平均数相等
9.点与圆上任一点连结的线段的中点的轨迹方程( )
A. B.
C. D.
10.两圆与的公共弦长等于( )
A. B. C. D.
11.若实数满足则的取值范围为( )
A. B. C. D.
12.已知点,,,直线将分割为面积相等的两部分,则的取值范围是( )
A.(0,) B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分)
13. =__________.
14.已知圆M与直线3x-4y=0及3x-4y+10=0都相切,圆心在直线y=-x-4上,则圆M的方程为____________.
15.阅读如下程序框图,运行相应的程序,则程序运行后输出的结果为 .
16.如图,已知直线与轴、轴分别交于,两点, 是以为圆心, 为半径的圆上一动点,连接,,则面积的最大值是
第Ⅱ卷
三、解答题(解答应写出文字说明,证明过程,或演算步骤)
17.(本题满分10分)
在锐角中,a,b,c分别为角A,B,C所对的边,且.
(Ⅰ) 确定角C的大小;
(Ⅱ) 若,且的周长为,求的面积.
18.(本题满分12分)
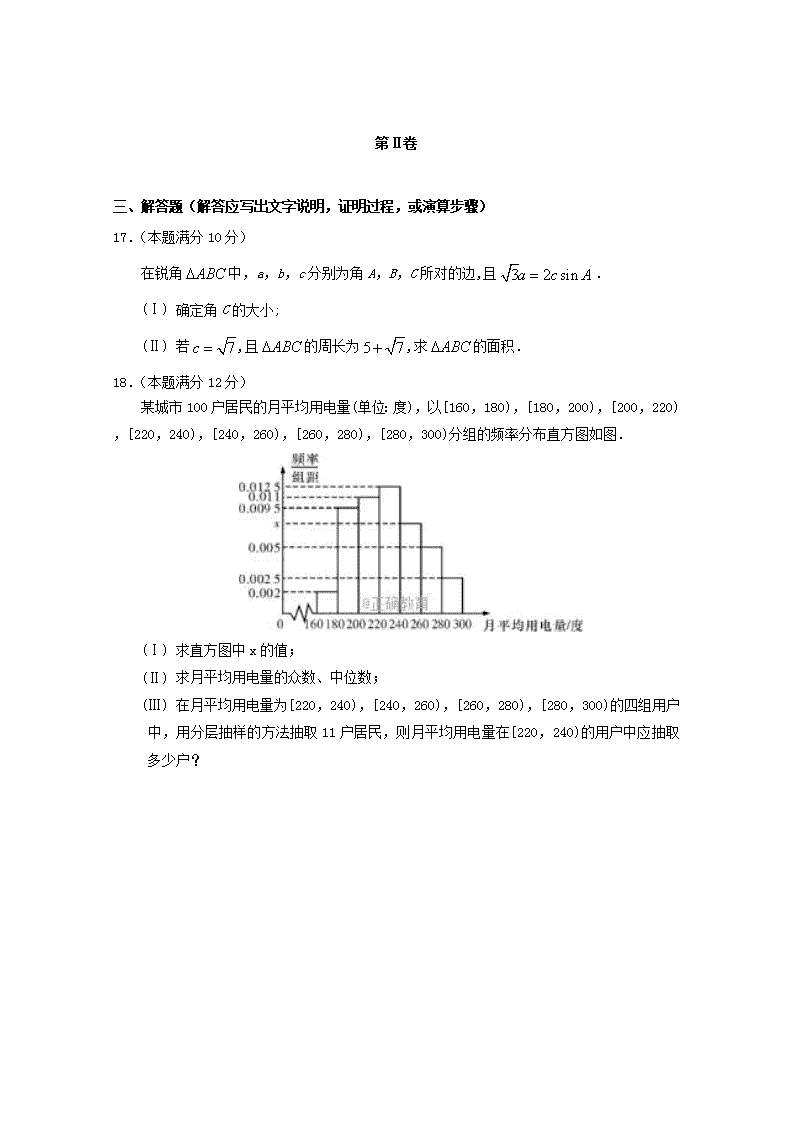
某城市100户居民的月平均用电量(单位:度),以[160,180),[180,200),[200,220),[220,240),[240,260),[260,280),[280,300)分组的频率分布直方图如图.
(Ⅰ) 求直方图中x的值;
(Ⅱ) 求月平均用电量的众数、中位数;
(Ⅲ) 在月平均用电量为[220,240),[240,260),[260,280),[280,300)的四组用户中,用分层抽样的方法抽取11户居民,则月平均用电量在[220,240)的用户中应抽取多少户?
19.(本题满分12分)
如图,AB是圆的直径,PA垂直圆所在的平面,C是圆上的点.
(Ⅰ)求证:平面PAC⊥平面PBC;
(Ⅱ)若AB=2,AC=1,PA=1,求二面角C-PB-A的余弦值.
20.(本题满分12分)
以下是某地搜集到的新房屋的销售价格和房屋的面积的数据:
(Ⅰ) 画出数据对应的散点图;
(Ⅱ) 求线性回归方程,并在散点图中加上回归直线;
(Ⅲ)据(Ⅱ)的结果估计当房屋面积为时的销售价格.
附:对于一组数据, ,…,其回归直线的斜率和截距的最小二乘估计分别为,
21.(本题满分12分)
如图,在平面直角坐标系中,已知圆及点
(Ⅰ)若直线平行于,与圆相交于两点, ,求直线的方程;
(Ⅱ)在圆上是否存在点,使得若存在, 求点的个数;若不存在,说明理由.
22.(本题满分12分)
已知各项均为正数的数列,满足 且.
(Ⅰ)求数列的通项公式;
(Ⅱ)设,若的前n项和为,求;
(Ⅲ)在(2)的条件下,求使成立的正整数n的最小值.
宜昌市葛洲坝中学2018-2019学年第一学期
高二年级期中考试试卷数学试题(理科) 答案
1—12. BDBAC CDCAD AB
13. 14. +=1 15. 9 16.
17.解:(1)因为,由正弦定理得,
因为,所以.
所以或. 因为是锐角三角形, 所以.
(2)因为,且的周长为,所以a+b=5 ①
由余弦定理得 ,即 ②
由②变形得,所以ab=6,得.
18. 解:(Ⅰ)由直方图的性质可得(0.002+0.009 5+0.011+0.012 5+x+0.005+0.002 5)×20=1,解方程可得x=0.007 5.
∴直方图中x的值为0.007 5;(2分)
(Ⅱ)月平均用电量的众数是=230,------(4分)
∵(0.002+0.009 5+0.011)×20=0.45<0.5,
∴月平均用电量的中位数在[220,240)内,
设中位数为a,由(0.002+0.009 5+0.011)×20+0.012 5×(a-220)=0.5可得a=224.
∴月平均用电量的中位数为224;--------(6分)
(Ⅲ)月平均用电量为[220,240)的用户有0.012 5×20×100=25,
月平均用电量为[240,260)的用户有0.007 5×20×100=15,
月平均用电量为[260,280)的用户有0.005×20×100=10,
月平均用电量为[280,300)的用户有0.002 5×20×100=5,
∴抽取比例为=,--------(11分)
∴月平均用电量在[220,240)的用户中应抽取25×=5(户).-------(12分)
19. 证明:(Ⅰ)由AB是圆的直径,得,
由平面ABC,平面ABC,得.
又,平面PAC,平面PAC,
所以平面PAC.
因为平面PBC,
所以平面PAC⊥平面PBC……………………………………………6分
(Ⅱ)解法一:过C作CM//AP,则CM⊥平面ABC.
如图(1),以点C为坐标原点,分别
以直线CB,CA,CM为x轴,y轴,z
轴建立空间直角坐标系.
第18题图(1)
在Rt△ABC中,因为AB=2,AC=1,
所以.
又因为PA=1,所以A(0,1, 0),B(,0,0),P(0,1,1).
故.
设平面BCP的法向量为,
则所以
不妨令,则.
因为
设平面ABP的法向量为,
则所以
不妨令,则.
于是.
由图(1)知二面角C-PB-A为锐角,
故二面角C-PB-A的余弦值为…………………………12分
(Ⅱ)解法二:如图(2),过C作CM⊥AB于M,
因为PA⊥平面ABC,平面ABC,
所以PA⊥CM.
又因为,且平面PAB,平面PAB,
所以CM⊥平面PAB.
过M作MN⊥PB于N,连接NC,
由三垂线定理得CN⊥PB,
所以∠CNM为二面角C-PB-A的平面角.
在Rt△ABC中,由AB=2,AC=1,
第18题图(2)
得,,.
在Rt△PAB中,由AB=2,PA=1,得.
因为Rt△BNM∽Rt△BAP,
所以,所以
所以在Rt△CNM中,,
所以,
所以故二面角C-PB-A的余弦值为…………………………12分
20.(1)数据对应的散点图如图所示:
(2),,
设所求回归直线方程为,
则,
故所求回归直线方程为
(3)据(2),当时,销售价格的估计值为:
(万元)
21. 解析:1.圆的标准方程为,
所以圆心,半径为.
因为,所以直线的斜率为,
设直线的方程为,
则圆心到直线的距离为
因为,
而,所以,
解得或,
故直线的方程为或.
2.假设圆上存在点,设,则,,
即,即,
因为
所以圆与圆相交, 所以点的个数为
22.解:(1)∵,
∵数列的各项均为正数,∴,
∴,即
所以数列是以2为公比的等比数列.
∵,∴数列的通项公式.
(2)由(1)及得,,
∵,
∴①
∴②
②-①得
(3)要使成立,只需成立,即,
∴使成立的正整数n的最小值为5.
附:双向细目表
高_二 _数学理_科期中考试命题双向细目表
题型
题号
考察知识点(非章节节点)
预估难度系数
能力要求
分值
备注
了解识记
理解
掌握
灵活运用
选择题
1
直线倾斜角月斜率
0.9
√
5
2
辗转相除法
0.9
√
5
3
直线的定点问题
0.9
√
5
4
圆的标准方程
0.9
√
5
5
抽样方法
0.9
√
5
6
样本的数字特征
0.8
√
5
7
圆的切线问题
0.7
√
5
8
茎叶图
0.8
√
5
9
求轨迹方程
0.7
√
5
10
两圆的位置关系
0.6
√
5
11
直线与圆的关系应用
0.6
√
5
12
直线的特征量的理解应用
0.4
√
5
填空题
13
k进制互化
0.8
√
5
14
相切类求圆的方程
0.7
√
5
15
程序框图
0.7
√
5
16
直线与圆的最值问题
0.6
√
5
解答题
17
解三角形
0.7
√
10
18
频率分布直方图、抽样方法
0. 8
√
12
19
线与面位置关系及计算
0.7
√
12
20
回归直线方程
0.8
√
12
21
直线与圆、圆与圆的位置关系
0.7
√
12
22
数列通项、求和及应用
0.6
√
12
整套试题的难度系数0.7