- 282.00 KB
- 2021-04-27 发布
2017-2018学年甘肃省平凉市静宁县第一中学高二上学期期中考试数学理试题
一、 选择题:(每题只有一个正确选项。共12个小题,每题5分,共60分。)
1.若命题“”为假,且“”为假,则( )
A.或为假 B.假 C.真 D.不能判断的真假
2.在△中,“”是“”的( )
A.充分不必要条件 B.必要不充分条件[.
C.充要条件 D.既不充分也不必要条件
3.双曲线8kx2-ky2=8的一个焦点是(0,3),则k的值是( )
A.-1 B.1 C. D.-
k=0,S=1
k<3
开始
结束
是
否
k=k+1
输出S
S=S×
(第4题图)
4.执行如图所示的程序框图,输出的S值为
( )
A.2
B.4
C.8
D.16
[]
5.动点到点及点的距离之差为,则点的轨迹是( )
A.双曲线 B.双曲线的一支 C.两条射线 D.一条射线
6.设F1,F2分别是椭圆C:+
=1(a>b>0)的左、右焦点,点P在椭圆C上,线段PF1的中点在y轴上,若∠PF1F2=30°,则椭圆的离心率为( )
A. B. C. D.[]
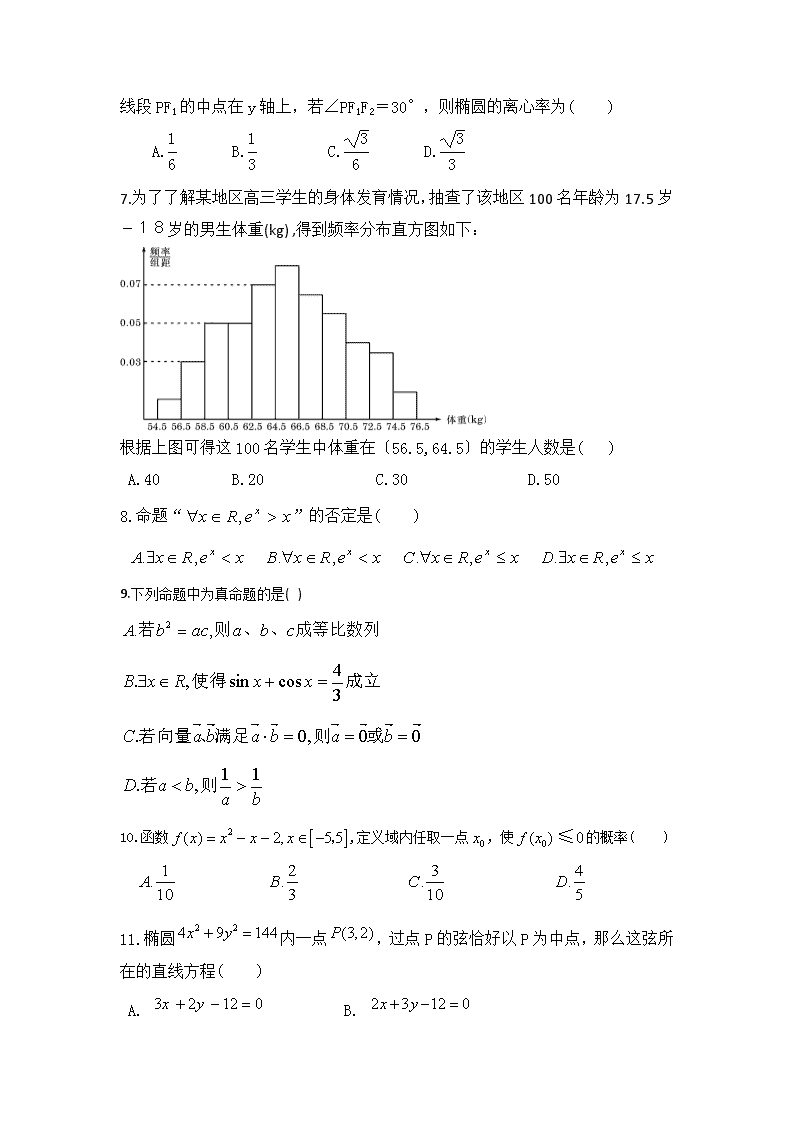
7.为了了解某地区高三学生的身体发育情况,抽查了该地区100名年龄为17.5岁-18岁的男生体重(kg) ,得到频率分布直方图如下:
根据上图可得这100名学生中体重在〔56.5,64.5〕的学生人数是( )
A.40 B.20 C.30 D.50
8.命题“”的否定是( )
9.下列命题中为真命题的是( )
10.函数,定义域内任取一点,使的概率( )
11.椭圆内一点,过点P的弦恰好以P为中点,那么这弦所在的直线方程( )
A. B.
C. D.
12.如图所示,F1,F2是双曲线-=1(a>0,b>0)的左、右焦点,过F1的直线l与双曲线的左、右两个分支分别交于B,A,若△ABF2为等边三角形,则该双曲线的离心率为( )
A. B. C.4 D.
二.填空题(共4个小题,每题5分,共20分。)
13.口袋内装有个大小相同的红球、白球和黑球,其中有个红球,从中摸出个球,若摸出白球的概率为,则摸出黑球的概率为____________.
14.若方程表示椭圆,则的取值范围是______________.
15. 已知是双曲线的左焦点,是双曲线右支上的动点,则的最小值为_ .
16.已知命题p:“∀x∈|1,2],x2+lnx-a≥0”与命题q:“∃x∈R,x2+2ax-8-6a=0”都是真命题,则实数a的取值范围是__________.
三、解答题:(本大题共6小题,共80分. 解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)若双曲线与椭圆有相同的焦点,与双曲线有相同渐近线,求双曲线方程.
18.学校从参加高一年级期中考试的学生中抽出50名学生,并统计了他们的数学成绩(成绩均为整数且满分为100分),数学成绩分组及各组频数如下:
[40,50),2;[50,60),3;[60,70),14;[70,80),15;[80,90),12;[90,100],4.
(1)在给出的样本频率分布表中,求A,B,C,D的值;
(2)估计成绩在80分以上(含80分)学生的比例;
(3)为了帮助成绩差的学生提高数学成绩,学校决定成立“二帮一”小组,即从成绩在[90,100]的学生中选两位同学,共同帮助成绩在[40,50)中的某一位同学.已知甲同学的成绩为42分,乙同学的成绩为95分,求甲、乙两同学恰好被安排在同一小组的概率.样本频率分布表如下:
分组
频数[]
频率
[40,50)
2
0.04
[50,60)
3
0.06[]
[60,70)
14
0.28
[70,80)
15
0.30
[80,90)
A
B
[90,100]
4
0.08
合计
C
D
19.(本小题满分12分)已知命题,;命题关于的方程有两个相异实数根.
(1)若为真命题,求实数的取值范围;
(2)若为真命题,求实数的取值范围.
20.(本小题满分12分)已知椭圆C:+=1(a>b>0)的一个顶点A(2,0),离心率为,直线y=k(x-1)与椭圆C交于不同的两点M,N.
(1)求椭圆C的方程;
(2)当△AMN的面积为时,求实数k的值.
21.已知集合A=,B={x|x+m2≥1}.若“x∈A”是“x∈B”的充分条件,求实数m的取值范围.
22.已知中心在原点的双曲线C的右焦点为,右顶点为.(Ⅰ)求双曲线C的方程 (Ⅱ)若直线与双曲线恒有两个不同的交点A和B且(其中为原点),求k的取值范围