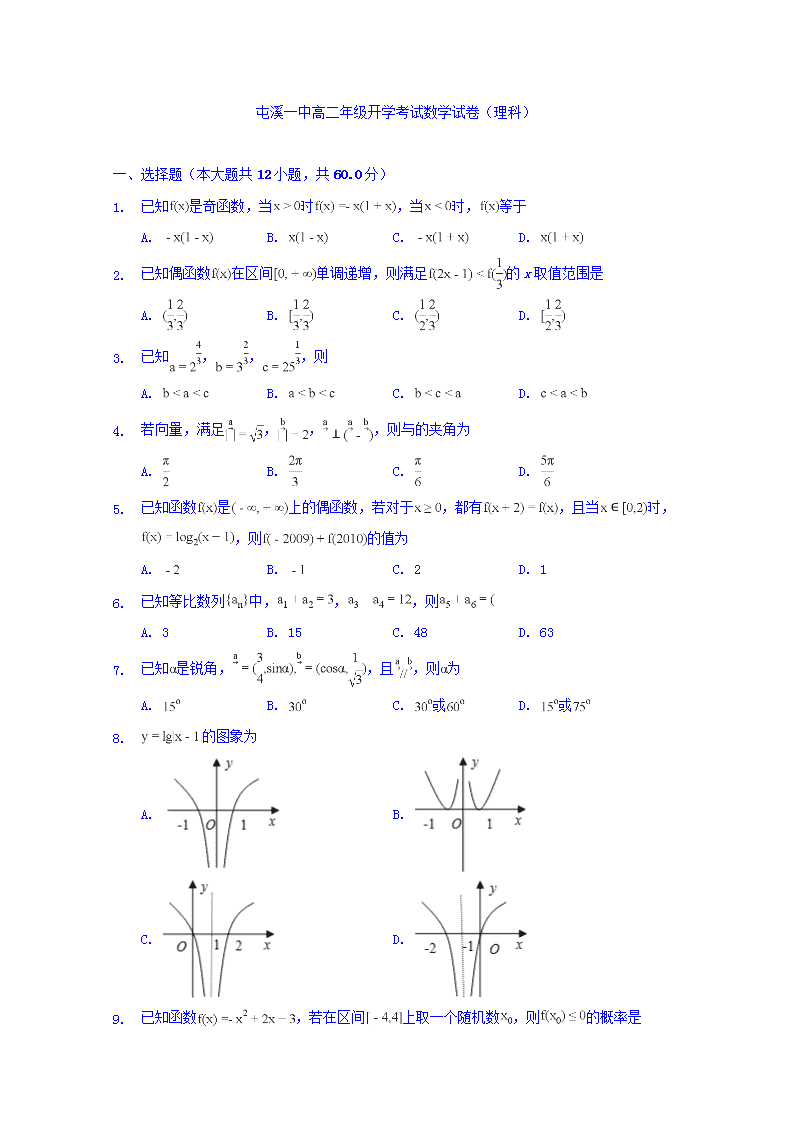- 772.50 KB
- 2021-04-27 发布
屯溪一中高二年级开学考试数学试卷(理科)
一、选择题(本大题共12小题,共60.0分)
1. 已知是奇函数,当时,当时,等于
A. B. C. D.
2. 已知偶函数在区间单调递增,则满足的x取值范围是
A. B. C. D.
3. 已知,,,则
A. B. C. D.
4. 若向量,满足,,,则与的夹角为
A. B. C. D.
5. 已知函数是上的偶函数,若对于,都有,且当时,,则的值为
A. B. C. 2 D. 1
6. 已知等比数列中,,,则
A. 3 B. 15 C. 48 D. 63
7. 已知是锐角,,且,则为
A. B. C. 或 D. 或
8. 的图象为
A. B.
C. D.
9. 已知函数,若在区间上取一个随机数,则的概率是
A. B. C. D.
1. 若,,且,则的最小值是
A. 2 B. C. D.
2. 设x,y满足约束条件则的取值范围是
A. B. C. D.
3. 已知函数满足:,且当时,,那么方程的解的个数为
A. 1个 B. 8个 C. 9个 D. 10个
二、填空题(本大题共4小题,共20.0分)
4. 已知集合,若集合A中只有一个元素,则实数a的取值为______ .
5. 已知向量,,则在方向上的投影等于______.
6. 设的内角A,B,C的对边分别为a,b,若,,,则 ______ .
7. 数列1,的前n项和为,则正整数n的值为______ .
三、解答题(本大题共6小题,共70分)
8. 已知等差数列的前n项和为,,.
求;
设数列的前n项和为,证明:.
1. 已知函数.
求的最小正周期;
求图象的对称轴方程和对称中心的坐标.
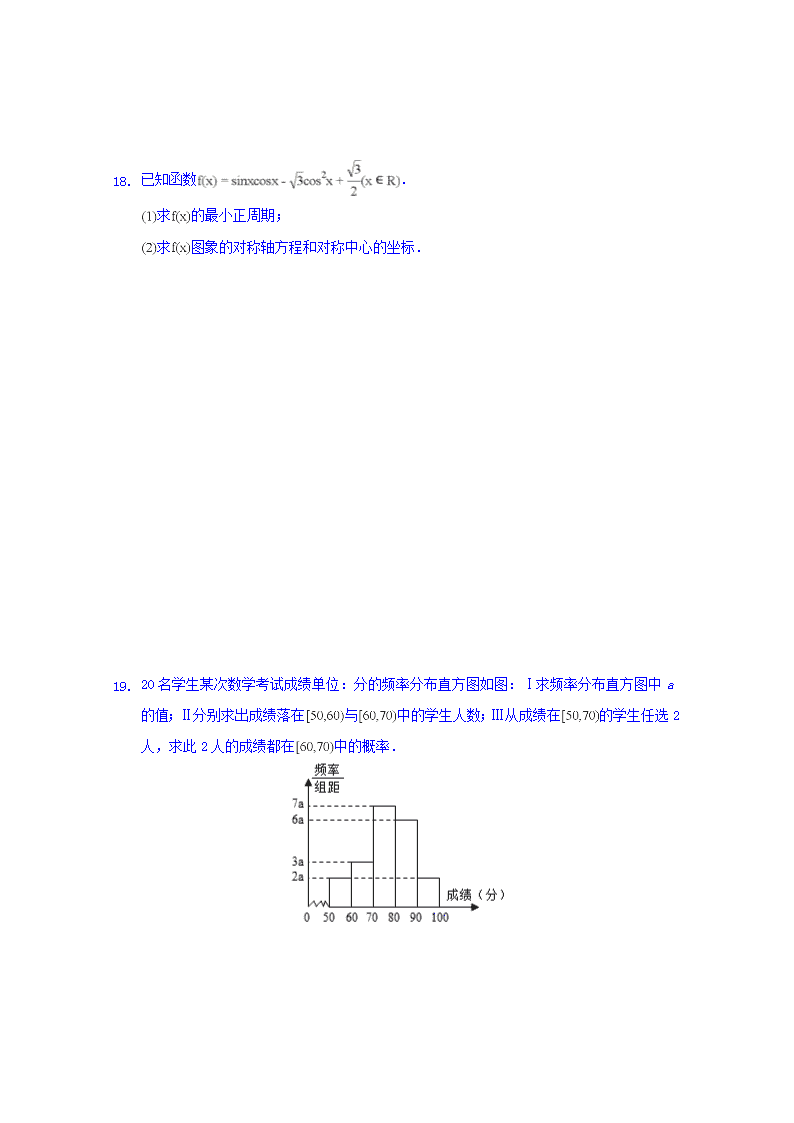
2. 20名学生某次数学考试成绩单位:分的频率分布直方图如图:Ⅰ求频率分布直方图中a的值;Ⅱ分别求出成绩落在与中的学生人数;Ⅲ从成绩在的学生任选2人,求此2人的成绩都在中的概率.
1. 已知a,b,c分别是内角A,B,C的对边,且满足.
求角A的大小;
若,,求的面积.
1. 已知函数,且时,总有成立.
求a的值;
判断并证明函数的单调性;
求在上的值域.
2. 设函数,其中.
若,求函数在区间上的取值范围;
若
,且对任意的,都有,求实数a的取值范围.
若对任意的,,都有,求t的取值范围.
一、选择题(本大题共12小题,共60.0分)
1. 已知是奇函数,当时,当时,等于
A. B. C. D.
解:当时,,
则.
又是R上的奇函数,所以当时.
故选项A正确.
2. 已知偶函数在区间单调递增,则满足的x取值范围是
A. B. C. D.
解:是偶函数,,
不等式等价为,
在区间单调递增,
,解得.
故选:A.
3. 已知,,,则
A. B. C. D.
解:,
,
,
综上可得:,
故选:A.
4. 若向量,满足,,,则与的夹角为
A. B. C. D.
解:设与的夹角为,,
,,,
,,,
故选:C.
1. 已知函数是上的偶函数,若对于,都有,且当时,,则的值为
A. B. C. 2 D. 1
解:数是上的偶函数,且对于,都有,
又当时,,
,
故选D.
2. 已知等比数列中,,,则
A. 3 B. 15 C. 48 D. 63
解:,,
,
,
.
故选C.
3. 已知是锐角,,且,则为
A. B. C. 或 D. 或
解:根据题意,,
若,则有,
即有,
又由是锐角,则有,
即或,
则或,
故选C.
1. 的图象为
A. B.
C. D.
可知函数的定义域为:或,函数的图象关于对称.
由函数的图象,可知,A、B、D不满足题意.
故选:C.
2. 已知函数,若在区间上取一个随机数,则的概率是
A. B. C. D.
令,可得或,则,或,时,.所求概率为.故选C.
1. 若,,且,则的最小值是
A. 2 B. C. D.
解:
当且仅当时,等号成立故选D
2. 设x,y满足约束条件则的取值范围是
A. B. C. D.
解:x,y满足约束条件的可行域如图:
目标函数,经过可行域的A,B时,目标函数取得最值,
由解得,
由解得,
目标函数的最大值为:2,最小值为:,
目标函数的取值范围:.
故选:B.
3. 已知函数满足:,且当时,,那么方程的解的个数为
A. 1个 B. 8个 C. 9个 D. 10个
解:函数满足:,
是周期为2的周期函数,
当时,,
作出和两个函数的图象,如下图:
结合图象,得:方程的解的个数为10个.
故选:D.
二、填空题(本大题共4小题,共20.0分)
1. 已知集合,若集合A中只有一个元素,则实数a的取值为______ .
解:因为集合有且只有一个元素,
当时,只有一个解,
当时,一元二次方程只有一个元素则方程有重根,即即.
所以实数或.
2. 已知向量,,则在方向上的投影等于______.
解:根据投影的定义可得:在方向上的投影为,.
故答案为:
3. 设的内角A,B,C的对边分别为a,b,若,,,则 ______ .
解:,
或 当时,,,,
由正弦定理可得, 则 当时,,与三角形的内角和为矛盾
故答案为:1
1. 数列1,的前n项和为,则正整数n的值为______ .
解:由题意可知,数列的通项
故答案为9
三、解答题(本大题共6小题,共72.0分)
2. 已知等差数列的前n项和为,,.
求;
设数列的前n项和为,证明:.
解:设等差数列的公差为d,
,
,,
,
;
证明:,
则
.
1. 已知函数.
求的最小正周期;
求图象的对称轴方程和对称中心的坐标.
解:函数
,
的最小正周期为;
函数,
令,,
解得,,
图象的对称轴方程为:,;
再令,,
解得,,
图象的对称中心的坐标为,.
2. 20名学生某次数学考试成绩单位:分的频率分布直方图如图:Ⅰ求频率分布直方图中a的值;Ⅱ分别求出成绩落在与中的学生人数;Ⅲ从成绩在的学生任选2人,求此2人的成绩都在中的概率.
解:Ⅰ根据直方图知组距,由,解得.Ⅱ成绩落在中的学生人数为,
成绩落在中的学生人数为.Ⅲ记成绩落在中的2人为A,B,成绩落在中的3人为C,D,E,则成绩在的学生任选2人的基本事件有AB,AC,AD,AE,BC,BD,BE,CD,CE,DE共10个,
其中2人的成绩都在中的基本事件有CD,CE,DE共3个,
故所求概率为.
1. 已知a,b,c分别是内角A,B,C的对边,且满足.
求角A的大小;
若,,求的面积.
解:,可得:,
由余弦定理可得:,
又,
由及正弦定理可得:,
,,由余弦定理可得:,
解得:,,
2. 已知函数,且时,总有成立.
求a的值;
判断并证明函数的单调性;
求在上的值域.
解:,,即,,.
函数为R上的减函数,
的定义域为 R,
任取,,且,
,.
即
函数为 R 上的减函数.
由知,函数在上的为减函数,
,
即,
即函数的值域为
1. 设函数,其中.
若,求函数在区间上的取值范围;
若,且对任意的,都有,求实数a的取值范围.
若对任意的,,都有,求t的取值范围.
解:因为,
所以在区间上单调减,在区间上单调增,且对任意的,都有,
若,则.
当时单调减,从而最大值,最小值.
所以的取值范围为;
当时单调增,从而最大值,最小值.
所以的取值范围为;
所以在区间上的取值范围为 分
“对任意的,都有”等价于“在区间上,”.
若,则,
所以在区间上单调减,在区间上单调增.
当,即
时,
由,得,
从而 .
当,即时,由,得,
从而.
综上,a的取值范围为区间 分
设函数在区间上的最大值为M,最小值为m,
所以“对任意的,,都有”等价于“”.
当时,,.
由,得.
从而 .
当时,,.
由,得
.
从而 .
当时,,.
由,得.
从而 .
当时,,.
由,得.
从而 .
综上,t的取值范围为区间