2020-2021青岛市高二数学上期中第一次模拟试题(及答案) 20页

2020-2021 青岛市高二数学上期中第一次模拟试题 ( 及答案 ) 一、选择题 1．执行右面的程序框图，若输入的 , ,a b k 分别为 1,2,3，则输出的 M ( ) A． 20 3 B． 7 2 C． 16 5 D． 15 8 2．一组数据如下表所示： x 1 2 3 4 y e 3e 4e 6e 已知变量 y 关于 x 的回归方程为 +0.5? bxy e ，若 5x ，则预测 y 的值可能为 ( ) A． 5e B． 11 2e C． 13 2e D． 7e 3．用电脑每次可以从区间 0,1 内自动生成一个实数，且每次生成每个实数都是等可能性 的，若用该电脑连续生成 3 个实数，则这 3 个实数都大于 1 3 的概率为（ ） A． 1 27 B． 2 3 C． 8 27 D． 4 9 4．在区间 上随机取两个数 ,x y，记 1p 为事件 “ 1 2 x y ”的概率， 2p 为事件 “ 1 2 x y ”的概率， 3p 为事件 “ 1 2 xy ”的概率，则 （ ） A． 1 2 3p p p B． 2 3 1p p p C． 3 1 2p p p D． 3 2 1p p p 5．某学校 10 位同学组成的志愿者组织分别由李老师和张老师负责，每次献爱心活动均需 该组织 4 位同学参加 . 假设李老师和张老师分别将各自活动通知的信息独立，随机地发给 4 位同学，且所发信息都能收到 . 则甲同学收到李老师或张老师所发活动通知的信息的概率为 （ ） A． 2 5 B． 12 25 C． 16 25 D． 4 5 6．我校高中生共有 2700 人, 其中高一年级 900 人, 高二年级 1200 人, 高三年级 600 人, 现采 取分层抽样法抽取容量为 135 的样本 , 那么高一、高二、高三各年级抽取的人数分别为 ( ) A．45,75,15 B．45,45,45 C．45,60,30 D．30,90,15 7．统计某校 n 名学生的某次数学同步练习成绩，根据成绩分数依次分成六组： 90,100 , 100,110 , 110,120 , 120,130 , 130,140 , 140,150 ，得到频率分布直方图 如图所示，若不低于 140 分的人数为 110. ① 0.031m ；② 800n ；③100 分以下的人数 为 60；④分数在区间 120,140 的人数占大半．则说法正确的是（ ） A．①② B．①③ C．②③ D．②④ 8．为计算 1 1 1 1 11 2 3 4 99 100S ⋯ ，设计了下面的程序框图，则在空白框中应填入 A． 1i i B． 2i i C． 3i i D． 4i i 9．已知 0, 0, 2,a b a b 则 1 4y a b 的最小值是 ( ) A． 7 2 B．4 C． 9 2 D．5 10．A 地的天气预报显示， A 地在今后的三天中，每一天有强浓雾的概率为 30%，现用随 机模拟的方法估计这三天中至少有两天有强浓雾的概率，先利用计算器产生 0 9 之间整数 值的随机数，并用 0，1，2，3， 4，5，6 表示没有强浓雾，用 7，8，9 表示有强浓雾，再 以每 3 个随机数作为一组，代表三天的天气情况，产生了如下 20 组随机数： 402 978 191 925 273 842 812 479 569 683 231 357 394 027 506 588 730 113 537 779 则这三天中至少有两天有强浓雾的概率近似为 ( ) A． 1 4 B． 2 5 C． 7 10 D． 1 5 11．6 件产品中有 4 件合格品， 2 件次品 .为找出 2 件次品，每次任取一个检验，检验后不放 回，则恰好在第四次检验后找出所有次品的概率为（ ） A． 3 5 B． 1 3 C． 4 15 D． 1 5 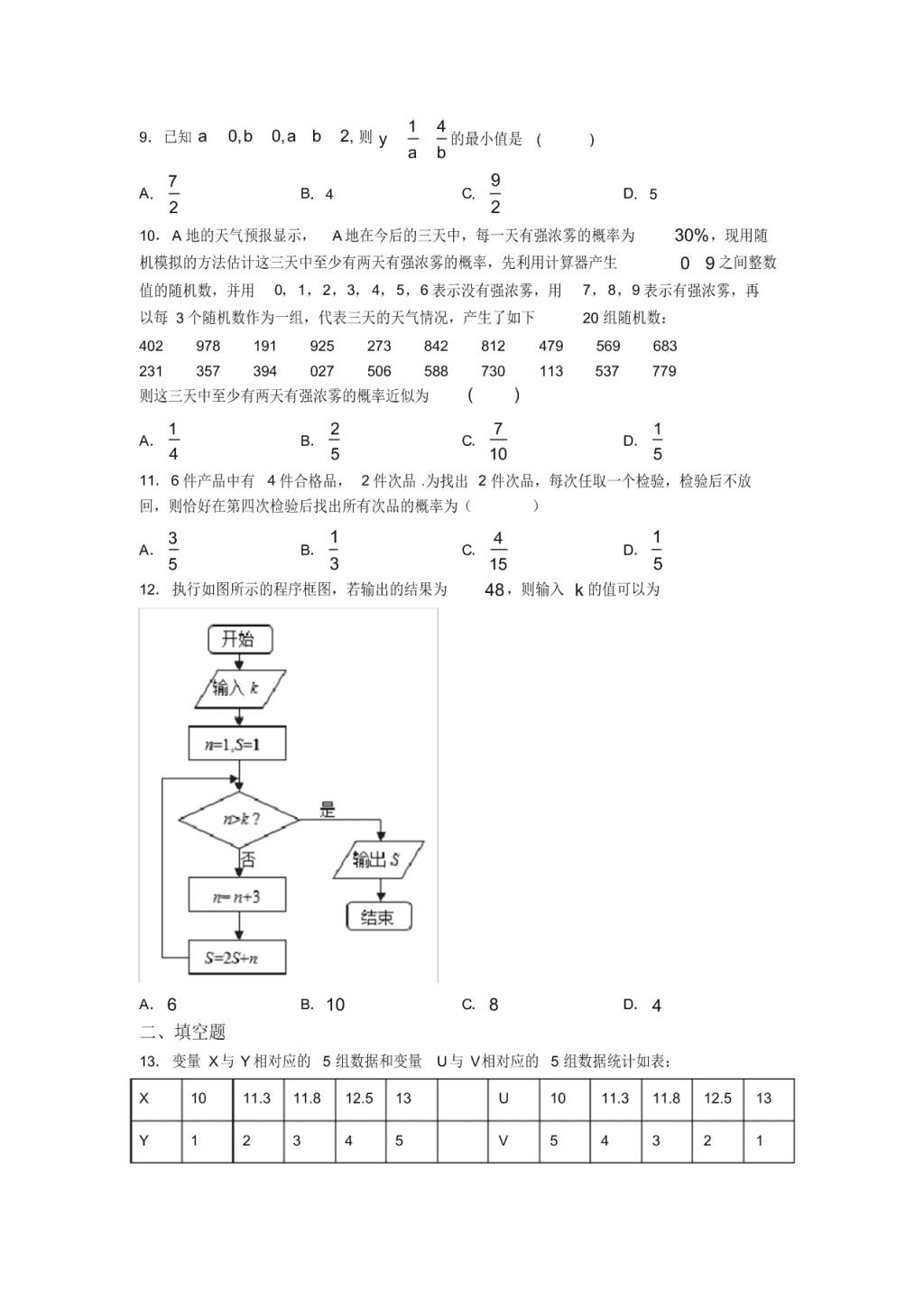12． 执行如图所示的程序框图，若输出的结果为 48，则输入 k 的值可以为 A． 6 B．10 C． 8 D． 4 二、填空题 13． 变量 X与 Y 相对应的 5 组数据和变量 U与 V相对应的 5 组数据统计如表： X 10 11.3 11.8 12.5 13 U 10 11.3 11.8 12.5 13 Y 1 2 3 4 5 V 5 4 3 2 1 用 b1 表示变量 Y与 X 之间的回归系数， b2 表示变量 V与 U之间的回归系数，则 b1 与 b2 的大 小关系是 ___． 14． 如图程序框图的算法思路源于我国古代数学名著《九章算术》中“更相减损术”．执 行该程序框图，若输入的 a，b 分别为 98、63，则输出的 a =_______． 15． 已知 0 1a ， 1 1b ，则关于 x 的方程 2 2 0x ax b 有实根的概率是 ______． 16． 用秦九韶算法计算多项式 f(x)=2x 4-x 3+3x2+7, 在求 x=2 时对应的值时 ,v 3 的值为 ___. 17． 课题组进行城市空气质量调查，按地域把 24 个城市分成甲、乙、丙三组，对应的城市 的个数分别为 4、12、8．若用分层抽样的方法抽取 6 个城市，则乙组中应抽取的城市数为 _________． 18． 以下说法正确的是 _____________ . ①类比推理属于演绎推理 . ②设有一个回归方程 ? 2 3y x ，当变量每增加 1 个单位， y 平均增加 3 个单位 . ③样本相关系数 r 满足以下性质： 1r ，并且 r 越接近 1，线性相关程度越强； r 越接 近 0，线性相关程度越弱 . ④对复数 1 2,z z 和自然数 n 有 1 2 1 2 n n nz z z z . 19． 计算机执行如图所示的程序后，输出的结果是 __________． 20． 正四面体的 4 个面上分别写着 1、2、3、4，将 3 个这样均匀的正四面体同时投掷于桌 面上，与桌面接触的 3 个面上的 3 个数的乘积能被 4 整除的概率是 _____________． 三、解答题 21． 某地实施乡村振兴战略，对农副产品进行深加工以提高产品附加值，已知某农产品成 本为每件 3 元，加工后的试营销期间，对该产品的价格与销售量统计得到如下数据： 单价 x（元） 6 6.2 6.4 6.6 6.8 7 销量 y（万件） 80 74 73 70 65 58 数据显示单价 x 与对应的销量 y 满足线性相关关系． （1）求销量 y（件）关于单价 x（元）的线性回归方程 ?? ?y bx a ； （2）根据销量 y 关于单价 x 的线性回归方程，要使加工后收益 P 最大，应将单价定为多少 元？（产品收益 =销售收入 -成本）． 参考公式： ?b = 1 2 1 ( ) ( ) n i ii n ii x x y y x x = 1 2 2 1 n i ii n ii x y nxy x nx ， ??a y bx 22． 某校高二八班学生每周用于数学学习的时间 x （单位： h）与数学成绩 y （单位：分） 之间有如下数据： x 24 15 23 19 16 11 20 16 17 13 y 92 79 97 89 64 47 83 68 71 59 某同学每周用于数学学习的时间为 18 小时，试预测该生数学成绩 .（保留小数点后两位） 参考数据 17.4x 74.9y 10 2 1 3182i i x 10 2 1 58375i i y 10 1 13578i i i x y ，参考 公式：回归直线的方程 $y bx a ，其中 1 1 2 22 1 1 , n n i i i i i i n n i i i i x x y y x y nx y b a y bx x x x nx . 23． 近年来，我国许多省市雾霾天气频发，为增强市民的环境保护意识，某市面向全市征 召 n 名义务宣传志愿者，成立环境保护宣传组织，现把该组织的成员按年龄分成 5组第 1组 [20,25) ，第 2 组 [25,30) ，第 3 组 [30,35) ，第 4 组 [35,40) ，第 5组 [40,45] ，得到的频 率分布直方图如图所示，已知第 2组有 35 人. （1）求该组织的人数； （2）若在第 3,4,5 组中用分层抽样的方法抽取 6名志愿者参加某社区的宣传活动，应从第 3,4,5组各抽取多少名志愿者？ （3）在（ 2）的条件下，该组织决定在这 6名志愿者中随机抽取 2 名志愿者介绍宣传经 验，求第 3组至少有 1名志愿者被抽中的概率 . 24． 现将甲、乙两个学生在高二的 6 次数学测试的成绩（百分制）制成如图所示的茎叶 图，进入高三后，由于改进了学习方法，甲、乙这两个学生的考试成绩预计同时有了大的 提升：若甲（乙）的高二任意一次考试成绩为 x ，则甲（乙）的高三对应的考试成绩预计 为 4x . （1）试预测：高三 6 次测试后，甲、乙两个学生的平均成绩分别为多少？谁的成绩更稳 定？ （2）若已知甲、乙两个学生的高二 6 次考试成绩分别由低到高进步的，定义 y 为高三的任 意一次考试后甲、乙两个学生的当次成绩之差的绝对值，求 y 的平均值 . 25． 为了调查教师对教育改革认识水平，现从某市年龄在 20,45 的教师队伍中随机选取 100 名教师，得到的频率分布直方图如图所示，若从年龄在 30,35 , 35,40 , 40,45 中用 分层抽样的方法选取 6 名教师代表． （1）求年龄在 35,40 中的教师代表人数； （2）在这 6 名教师代表中随机选取 2 名教师，求在 35,40 中至少有一名教师被选中的概 率． 26． 2019 年，河北等 8 省公布了高考改革综合方案将采取“ 3+1+2”模式，即语文、数 学、英语必考，然后考生先在物理、历史中选择 1 门，再在思想政治、地理、化学、生物 中选择 2 门 . 为了更好进行生涯规划，甲同学对高一一年来的七次考试成绩进行统计分析， 其中物理、历史成绩的茎叶图如图所示 . (1) 若甲同学随机选择 3 门功课，求他选到物理、地理两门功课的概率； (2) 试根据茎叶图分析甲同学应在物理和历史中选择哪一门学科？并说明理由； (3) 甲同学发现，其物理考试成绩 y ( 分) 与班级平均分 x ( 分) 具有线性相关关系，统计数据 如下表所示，试求当班级平均分为 50 分时，其物理考试成绩 . 参考数据 : 7 2 1 34840i i x ， 7 2 1 50767i i y ， 7 1 41964i i i x y ， 7 1 ( )( ) 314i i i x x y y . 参考公式： y bx a$ $ $ ， 1 1 22 2 1 1 ( )( ) ( ) n n i i i i i i n n i i i i x x y y x y n x y b x x x n x $ ， $a y b x$ (计算 $a b$，时精确到 0.01). 【参考答案】 *** 试卷处理标记，请不要删除 一、选择题 1．D 解析： D 【解析】 【分析】 【详解】 试题分析：根据题意由 1 3成立，则循环，即 1 3 31 , 2, , 2 2 2 2 M a b n ;又由 2 3 成立，则循环，即 2 8 3 82 , , , 3 3 3 2 3 M a b n ;又由 3 3 成立，则循环，即 3 3 15 8 15, , , 4 2 8 8 3 8 M a b n ;又由 4 3 不成立，则出循环，输出 15 8 M ． 考点：算法的循环结构 2．C 解析： C 【解析】 【分析】 令 lnz y$= ，求得 ,x z 之间的数据对照表，结合样本中心点的坐标满足回归直线方程，即 可求得 b ；再令 5x ，即可求得预测值 y . 【详解】 将式子两边取对数，得到 $ln 0.5y bx ，令 lnz y$= ，得到 0.5z bx ， 根据已知表格数据，得到 ,x z 的取值对照表如下： x 1 2 3 4 z 1 3 4 6 由上述表格可知： 1 2 3 4 2.5 4 x ， 1 3 4 6 3.5 4 z ， 利用回归直线过样本中心点，即可得 3.5 2.5 0.5b ， 求得 1.2b ，则 1.2 0.5z x ， 进而得到 $ 1.2 +0.5xy e ，将 5x 代入， 解得 13 6.5 2y e e . 故选： C. 【点睛】 本题考查利用样本中心点坐标满足回归直线方程求参数值，以及由回归方程进行预测值得 求解，属中档题 . 3．C 解析： C 【解析】 由题意可得： 每个实数都大于 1 3 的概率为 1 21 3 3 p ， 则 3 个实数都大于 1 3 的概率为 3 2 8 3 27 . 本题选择 C选项 . 4．B 解析： B 【解析】 【分析】 【详解】 因为 , [0,1]x y ，对事件 “ 1 2 x y ”，如图（ 1）阴影部分 ， 对事件 “ 1 2 x y ”，如图（ 2）阴影部分 ， 对为事件 “ 1 2 xy ”，如图（ 3）阴影部分 ， 由图知，阴影部分的面积从下到大依次是 ，正方形的面积为 ， 根据几何概型公式可得 2 3 1p p p ． （1） （2） （3） 考点：几何概型． 5．C 解析： C 【解析】 【分析】 甲同学收到李老师或张老师所发活动通知的信息的对立事件是甲同学既没收到李老师的信 息也没收到张老师的信息，李老师的信息与张老师的信息是相互独立的，由此可计算概 率． 【详解】 设甲同学收到李老师的信息为事件 A，收到张老师的信息为事件 B，A、B 相互独立， 4 2( ) ( ) 10 5 P A P B ， 则甲同学收到李老师或张老师所发活动通知的信息的概率为 3 3 161 ( ) 1 (1 ( ))(1 ( )) 1 5 5 25 P AB P A P B ． 故选 C． 【点睛】 本题考查相互独立事件的概率，考查对立事件的概率．在求两个事件中至少有一个发生的 概率时一般先求其对立事件的概率，即两个事件都不发生的概率．这样可减少计算，保证 正确． 6．C 解析： C 【解析】 因为共有学生 2700，抽取 135，所以抽样比为 135 2700 ，故各年级分别应抽取 135900 45 2700 ， 1351200 60 2700 ， 135600 30 2700 ，故选 C. 7．B 解析： B 【解析】 【分析】 根据频率分布直方图的性质和频率分布直方图中样本估计总体，准确运算，即可求解 . 【详解】 由题意，根据频率分布直方图的性质得 10( 0.020 0.016 0.016 0.011 0.006) 1m ， 解得 0.031m . 故①正确； 因为不低于 140 分的频率为 0.011 10 0.11，所以 110 1000 0.11 n ，故②错误； 由 100 分以下的频率为 0.006 10=0.06 ，所以 100 分以下的人数为 1000 0.06=60 ， 故③正确； 分数在区间 [120,140)的人数占 0.031 10 0.016 10 0.47，占小半 . 故④错误 . 所以说法正确的是①③. 故选 B. 【点睛】 本题主要考查了频率分布直方图的应用，其中解答熟记频率分布直方图的性质，以及在频 率分布直方图中，各小长方形的面积表示相应各组的频率，所有小长方形的面积的和等于 1，着重考查了分析问题和解答问题的能力，属于基础题 . 8．B 解析： B 【解析】 分析：根据程序框图可知先对奇数项累加，偶数项累加，最后再相减 . 因此累加量为隔项 . 详解：由 1 1 1 1 11 2 3 4 99 100 S 得程序框图先对奇数项累加，偶数项累加，最 后再相减 . 因此在空白框中应填入 2i i ，选 B. 点睛：算法与流程图的考查，侧重于对流程图循环结构的考查 . 先明晰算法及流程图的相关 概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终 止条件，更要通过循环规律，明确流程图研究的数学问题，是求和还是求项 . 9．C 解析： C 【解析】 【分析】 由题意结合均值不等式的结论即可求得 1 4y a b 的最小值，注意等号成立的条件 . 【详解】 由题意可得： 1 4y a b 1 1 4 1 45 2 2 b aa b a b a b 1 45 2 2 b a a b 9 2 ， 当且仅当 2 4, 3 3 a b 时等号成立 . 即 1 4y a b 的最小值是 9 2 . 故选： C. 【点睛】 在应用基本不等式求最值时，要把握不等式成立的三个条件，就是 “一正 —— 各项均为正； 二定 —— 积或和为定值；三相等 —— 等号能否取得 ”，若忽略了某个条件，就会出现错误． 10．D 解析： D 【解析】 【分析】 由题意知模拟这三天中至少有两天有强浓雾的结果，经随机模拟产生了如下 20 组随机数， 在 20 组随机数中表示三天中恰有两天有强浓雾的有可以通过列举得到共 4 组随机数，根据 概率公式，得到结果． 【详解】 由题意知模拟这三天中至少有两天有强浓雾的结果，经随机模拟产生了如下 20 组随机数， 在 20 组随机数中表示三天中恰有两天有强浓雾的有， 可以通过列举得到共 5 组随机数： 978，479、588、779，共 4 组随机数， 所求概率为 4 1 20 5 ， 故选 D． 【点睛】 本题考查模拟方法估计概率，解题主要依据是等可能事件的概率，注意列举法在本题的应 用． 11．C 解析： C 【解析】 【分析】 题目包含两种情况：第一种是前面三次找出一件次品，第四次找出次品，第二种情况是前 面四次都是正品，则剩余的两件是次品，计算概率得到答案 . 【详解】 题目包含两种情况： 第一种是前面三次找出一件次品，第四次找出次品， 2 3 1 4 6 1 5 Cp C ； 第二种情况是前面四次都是正品，则剩余的两件是次品， 4 4 2 4 6 1 15 Cp C ； 故 1 2 4 15 p p p . 故选： C . 【点睛】 本题考查了概率的计算，忽略掉前面四次都是正品的情况是容易发生的错误 . 12．C 解析： C 【解析】 【分析】 执行如图所示的程序框图，逐次循环，计算其运算的结果，根据选项即可得到答案 . 【详解】 由题意可知，执行如图所示的程序框图，可知： 第一循环： 1 3 4, 2 1 4 6n S ； 第二循环： 4 3 7, 2 6 7 19n S ； 第三循环： 7 3 10, 2 19 10 48n S ， 要使的输出的结果为 48，根据选项可知 8k = ，故选 C. 【点睛】 本题主要考查了循环结构的计算与输出问题，其中解答中正确理解循环结构的程序框图的 计算功能，逐次准确计算是解答的关键，着重考查了运算与求解能力，属于基础题 . 二、填空题 13．【解析】分析：根据回归系数几何意义得详解：因为 Y与 X之间正增长所以 因为 V与 U之间负增长所以因此点睛：函数关系是一种确定的关系相关关系是一 种非确定的关系事实上函数关系是两个非随机变量的关系而相关关系是 解析： 1 2b b . 【解析】 分析：根据回归系数几何意义得 1 20b b 详解：因为 Y 与 X 之间正增长，所以 1 0b 因为 V 与 U之间负增长，所以 2 0b 因此 1 20b b ， 点睛：函数关系是一种确定的关系，相关关系是一种非确定的关系 . 事实上，函数关系是两 个非随机变量的关系，而相关关系是非随机变量与随机变量的关系 . 如果线性相关，则直接 根据用公式求 $,a b$，写出回归方程，回归直线方程恒过点 ( , )x y . b$ 的正负，决定正相关与 负相关 . 14．7【解析】【分析】模拟执行程序框图只要按照程序框图规定的运算方法逐 次计算直到达到输出条件即可得到输出的值【详解】由程序框图可知：则因此 输出的为故答案为 7【点睛】本题主要考查程序框图的循环结构流程图属 解析： 7 【解析】 【分析】 模拟执行程序框图，只要按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 得到输出 a 的值 . 【详解】 由程序框图可知： 98 63a b ， 35 98 63, 28 63 35a b ， 7 35 28, 21 28 7a b ， 14 21 7, 7 21 14a b ， 7 14 7a ，则 7a b ，因此输出的 a 为 7 ，故答案为 7. 【点睛】 本题主要考查程序框图的循环结构流程图，属于中档题 . 解决程序框图问题时一定注意以下 几点： (1) 不要混淆处理框和输入框； (2) 注意区分程序框图是条件分支结构还是循环结 构； (3) 注意区分当型循环结构和直到型循环结构； (4) 处理循环结构的问题时一定要正确 控制循环次数； (5) 要注意各个框的顺序 ,（6）在给出程序框图求解输出结果的试题中只要 按照程序框图规定的运算方法逐次计算，直到达到输出条件即可 . 15．【解析】【分析】有实根则由根的判别式大于零可得之间的关系利用面积 型概率求解【详解】关于 x 的方程有实根则故答案为【点睛】本题是一道关于 几何概型问题的题目根据题意求出判别式大于零的情况满足条件然后结合图 解析： 1 4 【解析】 【分析】 有实根则由根的判别式大于零，可得 a 、 b 之间的关系，利用面积型概率求解 【详解】 1 1aQ ， 1 1b ， 2 2 4uS ， Q 关于 x 的方程 2 2 0x ax b 有实根 2 24 0a b ， 2 2 0a b a b 12 1 1 1 2qS 则 1 4 p 故答案为 1 4 【点睛】 本题是一道关于几何概型问题的题目，根据题意求出判别式大于零的情况满足条件，然后 结合图像求出面积即可得到结果，较为基础 16．【解析】 f(x)=2x4-x3+3x2+7=(((2x- 1)x+3)x)x+7 ∴v0=2v1=2×2 - 1=3v2=3×2+3=9v3=9×2=18 故答案为： 18 解析： 【解析】 f ( x)=2 x4- x3+3x2+7=(((2 x-1) x+3) x) x+7， ∴v0=2, v1=2×2 -1=3, v2=3×2+3=9, v3=9×2=18. 故答案为： 18. 17．3【解析】分析：根据分层抽样的方法各组抽取数按比例分配详解：根据分 层抽样的方法乙组中应抽取的城市数为点睛：本题考查分层抽样概念并会根据 比例关系确定各组抽取数 解析： 3 【解析】 分析：根据分层抽样的方法，各组抽取数按比例分配 . 详解：根据分层抽样的方法，乙组中应抽取的城市数为 126 =3 4+12+8 . 点睛：本题考查分层抽样概念，并会根据比例关系确定各组抽取数 . 18．③④【解析】分析：①根据类比推理与演绎推理的定义即可判断；②根据 回归方程的表达式即可判断；③利用线性相关指数的意义即可判断；④根据复 数的乘法运算律即可判断详解：对于①类比推理是合情推理的重要形式则不 解析： ③④ 【解析】 分析：①根据类比推理与演绎推理的定义即可判断；②根据回归方程的表达式，即可判 断；③利用线性相关指数 r 的意义即可判断；④根据复数的乘法运算律即可判断 . 详解：对于①，类比推理是合情推理的重要形式，则不属于演绎推理，故①错误； 对于②，根据回归方程为 ? 2 3y x ，可得当变量每增加 1 个单位， y 平均减少 3 个单 位，故②错误； 对于③，在回归分析中， r 具有以下性质： 1r ，并且 r 越接近 1，线性相关程度越 强； r 越接近 0，线性相关程度越弱，故③正确； 对于④，根据复数的乘法运算律，对复数 1 2,z z 和自然数 n 有 1 2 1 2 n n nz z z z ，故④正 确. 故答案为③④ . 点睛：本题考查了命题的真假判断与应用，考查相关关系及复数的运算，是一个考查的知 识点比较多的题目，解题本题的关键是理解概念及掌握运算公式，如在回归分析中， r 具 有的性质，复数遵循的运算律等． 19．3【解析】根据伪代码所示的顺序程序中各变量的值如下 :循环前 :n=5s=0;第 一次循环 :s=5n=4;第二次循环 :s=9n=3;输出此时的 n值为 3故填3 解析： 3 【解析】 根据伪代码所示的顺序 , 程序中各变量的值如下 : 循环前 :n=5 ,s=0; 第一次循环 :s=5 ,n=4; 第二次循环 :s=9 ,n=3; 输出此时的 n 值为 3, 故填 3. 20．【解析】将 3 个正四面体同时投掷于桌面时共有种情况与桌面接触的 3 个 面上的 3 个数的乘积能被 4 整除时则这 3 个数的乘积为 4 的倍数（ 1）这 3 个数 为 122 时有 3 种情况；（ 2）这 3 个数为 124 时有种；（ 3）这 3 个 解析： 11 16 【解析】 将 3 个正四面体同时投掷于桌面时，共有 34 64 种情况，与桌面接触的 3 个面上的 3 个 数的乘积能被 4 整除时，则这 3 个数的乘积为 4 的倍数，（ 1）这 3 个数为 1,2,2 时，有 3 种情况；（ 2）这 3 个数为 1,2,4 时，有 3 3 =6A 种；（ 3）这 3 个数为 1,3,4 时，有 3 3 =6A 种；（ 4）这 3 个数为 1,1,4 时，有 3 种；（ 5）这 3 个数为 2，2,2 时，有 1 种；（ 6）这 3 个数为 2,2,3 时，有 3 种；（ 7）这 3 个数为 2,2,4 时，有 3 种；（ 8）这 3 个数为 1,4,4 时， 有 3 种；（ 9）这 3 个数为 2,3,4 时，有 3 3 =6A 种；（ 10）这 3 个数为 2,4,4 时，有 3 种； （11）这 3 个数为 3,3,4 时，有 3 种；（ 12）这 3 个数为 3,4,4 时，有 3 种；（ 13）这 3 个 数为 4,4,4 时，有 1 种。故共有 3+6+6+3+1+3+3 3 6 3 3+3+1=44 种，故与桌面接 触的 3 个面上的 3 个数的乘积能被 4 整除的概率为 44 11= = 64 16 P 。 点睛：本题主要考查古典概型求概率，属于易错题。在求与桌面接触的 3 个面上的 3 个数 的乘积能被 4 整除时，采用分类讨论法，注意要做到不重不漏。 三、解答题 21． （1） ? 20 200y x ；（ 2）6.5 元 . 【解析】 【分析】 （1）由题意计算平均数和回归系数，即可写出回归直线方程； （2）由题意写出收益函数 P 的解析式，求出 P 取最大值时对应的 x 值即可． 【详解】 解：（ 1）由题意得， x = 1 6 ×（6+6.2+6.4+6.6+6.8+7 ）=6.5， y = 1 6 ×（80+74+73+70+65+58 ） =70； 则 6 1 ( ) 5 1.2 0.3 0 1.5 6 14i i i x x y y ， 6 2 1 ( ) 0.25 0.09 0.01 0.01 0.09 0.25 0.7i i x x ； 所以 14 20 0 7 ? . b ， 70 20 6.5 200??a y bx 所以所求回归直线方程为 20 200?y x ． （2）由题意可得， 3 20 2? 00 3P y x x x ， 整理得 P=-20（x-6.5） 2+245， 当 x=6.5 时， P 取得最大值为 245； 所以要使收益达到最大，应将价格定位 6.5 元． 【点睛】 本题考查了线性回归方程的求法与应用问题，也考查了计算与推理能力，是基础题． 22． 77.02 【解析】 【分析】 根据公式计算得到 3.53b ， 13.48a ， $ 3.53 13.48y x ，再代入数据计算得到答案 . 【详解】 1 222 1 13578 10 17.4 74.9 545.4 3.53 3182 10 17.4 154.4 n i i i n i i x y nx y b x nx ， 故 74.9 3.53 17.4 13.48a y bx ，故 $ 3.53 13.48y x . 当 18x 时， $ 3.53 18 13.48 77.02y . 【点睛】 本题考查了线性回归方程，意在考查学生的计算能力和应用能力 . 23． （1）100 （2）应从第 3,4,5 组中分别抽取 3 人， 2人， 1人 . （3） 4 5 【解析】 试题分析：（ 1）由题意第 2 组的人数为 35 5 0.07 n ，即可求解该组织人数 . （2）根据频率分布直方图，求得第 3 组，第 4 组，，第 5 组的人数，再根据分层抽样的方 法，即可求解再第 3,4,5 组所抽取的人数 . （3）记第 3组的 3 名志愿者为 1 2 3, ,A A A ，第 4 组的 2 名志愿者为 1 2,B B ，第 5 组的 1名志 愿者为 1C ，列出所有基本事件的总数，得出事件所包含的基本事件的个数，利用古典概 型，即可求解概率 . 试题解析： （1）由题意第 2 组的人数为 35 5 0.07 n ，得到 100n ，故该组织有 100人. （2）第 3组的人数为 0.06 5 100 30 ，第 4 组的人数为 0.04 5 100 20 ，第 5 组的 人数为 0.02 5 100 10，所以第 3,4,5 组共有名志愿者，所以利用分层抽样的方法在 60 名志愿者中抽取 6名志愿者，每组抽取的人数分别为：第 3组 30 6 3 60 ；第 4 组 20 6 2 60 ；第 5组 10 6 1 60 . 所以应从第 3,4,5 组中分别抽取 3 人， 2人， 1人. （3）记第 3组的 3 名志愿者为 1 2 3, ,A A A ，第 4 组的 2 名志愿者为 1 2,B B ，第 5 组的 1名志 愿者为 1C ，则从 6名志愿者中抽取 2 名志愿者有 1 2 1 3 1 1, , , , , ,A A A A A B 1 2 1 1, , , ,A B A C 2 3 2 1, , , ,A A A B 2 2, ,A B 2 1, ,A C 3 1 3 2 3 1, , , , , ,A B A B A C 1 2 1 1 2 1, , , , ,B B B C B C ，共 15有种 . 其中第 3 组的 3 名志愿者 1 2 3, ,A A A 至少有一名志愿者被抽中的有 1 2 1 3 1 1 1 2, , , , , , , ,A A A A A B A B 1 1, ,A C 2 3 2 1 2 2 2 1, , , , , , , ,A A A B A B A C 3 1 3 2 3 1, , , , ,A B A B A C ，共 12有种 . 则第 3 组至少有 1名志愿者被抽中的概率为 12 4 15 5 . 24． （1）见解析；（ 2）2 【解析】 【分析】 （1）由茎叶图计算高二 6 次考试的甲乙平均成绩，再分别加 4 即为高三平均成绩；（ 2） 列举甲、乙两个学生的当次成绩之差的绝对值，再计算均值即可 【详解】 （1）甲高二的 6 次考试平均成绩为 68 76 79 86 88 95 82 6 ， 乙高二的 6 次考试平均成绩为 71 75 82 84 86 94 82 6 ， 所以预测甲高三的 6 次考试平均成绩为 86，乙高三 6 次考试平均成绩为 86， 甲高三的 6 次考试平均成绩的方差为 2 2 2 2 2 2 72 86 80 86 83 86 90 86 92 86 99 86 77 6 . 乙高三的 6 次考试平均成绩的方差为 2 2 2 2 2 2 75 86 79 86 86 86 88 86 90 86 99 86 55.7 6 . 因为 77>55.7 ，所以乙的成绩比较稳定 . （2）预测高三的 6 次考试成绩如下： 第 1 次考 试 第 2 次考 试 第 3 次考 试 第 4 次考 试 第 5 次考 试 第次 6 考 试 甲 72 80 83 90 92 99 乙 75 79 86 88 90 98 因为 y 为高三的任意一次考试后甲、乙两个学生的当次成绩之差的绝对值， 所以 y 的值依次为 3,1,3,2,2,1 ， 所以 y 的平均值为 2 1 2 3 2 6 . 【点睛】 本题考查茎叶图中的均值，熟记茎叶图均值的计算方法，准确计算是关键，是基础题 . 25． （1）2 名；（ 2） 3 5 【解析】 【分析】 （1）根据分层抽样的比例关系计算得到答案 . （2）记在 35,40 中选取 2 名教师代表为 a，b，其余的 4 名代表为 A、B、C、D，列出所 有情况和满足条件的情况，相除得到答案 . 【详解】 （1）由频率分布直方图得： 年龄在 30,35 的教师有 100 0.06 5 30， 年龄在 35,40 的教师有 100 0.04 5 20， 年龄在 40,45 的教师有 100 0.02 5 10， 设年龄在 35,40 的教师代表人数为 x，则 6 60 20 x ，∴ 2x ∴从年龄在 35,40 中选取教师代表人数为 2 名； （2）记在 35,40 中选取 2 名教师代表为 a，b，其余的 4 名代表为 A、B、C、D 从这 6 名教师中选 2 名教师的选法为： ab， aA，aB，aC，aD， bA，bB，bC， bD， AB，AC，AD ， BC，BD， CD 以上共 15 种 在 35,40 中至少有一名教师被选中的选法为： ab， aA，aB，aC，aD， bA，bB，bC， bD 以上 9 种 在 35,40 中至少有一名教师被选中为事件 A，则 9 3 15 5 P A . ∴在 [35，40）中至少有一名教师被选中的概率为 3 5 . 【点睛】 本题考查了频率直方图，分层抽样，概率的计算，意在考查学生的综合应用能力 . 26． （1） 1 4 ；（ 2）见解析；（ 3）见解析 【解析】 【分析】 (1)列出基本事件的所有情况，然后再列出满足条件的所有情况，利用古典概率公式即可得 到答案 . (2)计算平均值和方差，从而比较甲同学应在物理和历史中选择哪一门学科； （3）先计算 x 和 y ，然后通过公式计算出线性回归方程，然后代入平均值 50 即可得到答 案 . 【详解】 (1) 记物理、历史分别为 1 2,A A ，思想政治、地理、化学、生物分别为 1 2 3 4, , ,B B B B ， 由题意可知考生选择的情形有 1 1 2, ,A B B ， 1 1 3, ,A B B ， 1 1 4, ,A B B ， 1 2 3, ,A B B ， 1 2 4, ,A B B ， 1 3 4, ,A B B ， 2 1 2, ,A B B ， 2 1 3, ,A B B ， 2 1 4, ,A B B ， 2 2 3, ,A B B ， 2 2 4, ,A B B ， 2 3 4, ,A B B ，共 12 种 他选到物理、地理两门功课的满情形有 1 1 2 1 2 3 1 2 4, , , , , ,A B B A B B A B B ，共 3 种 甲同学选到物理、地理两门功课的概率为 3 1 12 4 P (2) 物理成绩的平均分为 76 82 82 85 87 90 93 85 7 x物理 历史成绩的平均分为 69 76 80 82 94 96 98 85 7 x历史 由茎叶图可知物理成绩的方差 2s 物理 历史成绩的方差 2s 物理 故从平均分来看，选择物理历史学科均可以；从方差的稳定性来看，应选择物理学科；从 最高分的情况来看，应选择历史学科 ( 答对一点即可 ) (3) 57+61+65+72+74+77+84 70 7 x ， 85y , 7 1 7 22 2 1 7 41964 7 70 85 314 0.58 34840 7 70 540 ? 7 i ii ii x y x y b x x 85 0.58 70 44.? 0? 4a y b x y 关于 x 的回归方程为 0.58 +44.40y x 当 50x 时， 0.58 50+44.40 73y , 当班级平均分为 50 分时，其物理考试成绩为 73 分 【点睛】 本题主要考查古典概型，统计数的相关含义，线性回归方程的计算，意在考查学生的阅读 理解能力，计算能力和分析能力，难度不大 .