宁夏吴忠中学2019-2020学年高一下学期期中考试数学试题 19页

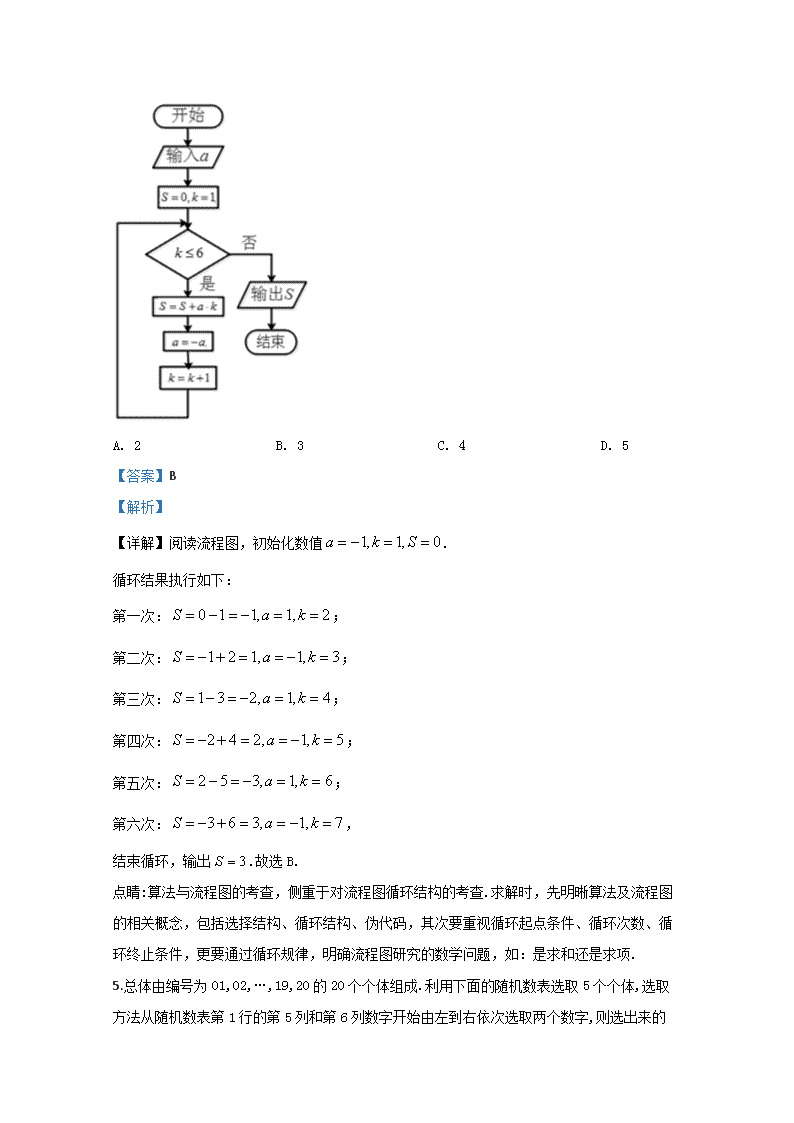
吴忠中学2019—2020学年第二学期期中考试 高一年级数学试卷 考试时间100分钟 满分120‎ 一、选择题：本大题共12个小题，每小题4分，共48分.在每小题给出的四个选项中，只有一项是符合题目要求的.‎ ‎1.阅读如图所示的程序，则循环体被执行的次数是（ ）‎ A. 4 B. ‎5 ‎C. 6 D. 7‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据框图的流程依次写出每次循环得到的、，由此得出循环体的执行次数.‎ ‎【详解】， ‎ 当，满足，则，，‎ 当，满足，则，，‎ 当，满足，则，， ‎ 当，满足，则，， ‎ 当，满足，则，，‎ 此时不满足，结束循环，执行循环体，故共执行5次.‎ 故选：B ‎【点睛】本题考查了循环语句中的当循环，写出每次循环结果是解决此类问题的基本方法，属于基础题.‎ ‎2.下列各式中不能化简为的是（　　）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ 由向量运算的三角形法则可得，所以答案A正确；由于，所以答案B正确；又因为，所以答案C 正确，应选答案D．‎ ‎3.给出下列命题：‎ ‎①两个具有公共终点的向量，一定是共线向量.‎ ‎②两个向量不能比较大小，但它们的模能比较大小.‎ ‎③（为实数），则必为零.‎ ‎④为实数，若，则与共线.‎ 其中正确的命题的个数为( )‎ A. 1 B. ‎2 ‎C. 3 D. 4‎ ‎【答案】A ‎【解析】‎ 因为两个向量终点相同，起点若不在一条直线上，则也不共线，命题错误；由于两个向量不能比较大小，但它们的模能比较大小，因此命题是正确的；若（为实数），则也可以零，因此命题也是错误的；若为0，尽管有，则与也不一定共线，即命题也是错误的，应选答案A．‎ ‎4.执行如图所示的程序框图，如果输入的，则输出的 ‎ A. 2 B. ‎3 ‎C. 4 D. 5‎ ‎【答案】B ‎【解析】‎ ‎【详解】阅读流程图，初始化数值. ‎ 循环结果执行如下：‎ 第一次：；‎ 第二次：；‎ 第三次：；‎ 第四次：；‎ 第五次：；‎ 第六次：，‎ 结束循环，输出.故选B.‎ 点睛:算法与流程图的考查，侧重于对流程图循环结构的考查.求解时，先明晰算法及流程图的相关概念，包括选择结构、循环结构、伪代码，其次要重视循环起点条件、循环次数、循环终止条件，更要通过循环规律，明确流程图研究的数学问题，如：是求和还是求项.‎ ‎5.‎ 总体由编号为01,02,…,19,20的20个个体组成.利用下面的随机数表选取5个个体,选取方法从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字,则选出来的第5个个体的编号为( )‎ A. 08 B. ‎07 ‎C. 02 D. 01‎ ‎【答案】D ‎【解析】‎ 试题分析：从随机数表第1行的第5列和第6列数字开始由左到右依次选取两个数字中小于20的编号依次为08，02，14，07，02，01，．其中第二个和第四个都是02，重复．‎ 可知对应的数值为08，02，14，07，01，‎ 则第5个个体的编号为01‎ 考点：随机抽样 ‎6.某企业三月中旬生产A、B、C三种产品共3 000件，根据分层抽样的结果，企业统计员制作了如下的统计表格：‎ 产品类别 A B C 产品数量（件）‎ ‎1 300‎ 样本容量（件）‎ ‎130‎ 由于不小心，表格中A、C产品的有关数据已被污染看不清楚，统计员记得A产品的样本容量比C产品的样本容量多10，根据以上信息，可得C的产品数量是（ ）‎ A. 80 B. ‎800 ‎C. 90 D. 900‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 根据B的样本容量为130，求得ABC的样本容量，进而得到AC的样本容量，然后根据A产品的样本容量比C产品的样本容量多10，求得C的样本容量，进而得到C的产品数量.‎ ‎【详解】设样本容量为x，则，‎ 所以.‎ 所以A产品和C产品在样本中共有（件）.‎ 设C产品的样本容量为y，则，‎ 所以.‎ 所以C产品的数量为.‎ 故选：B ‎【点睛】本题主要考查分层抽样，还考查了理解辨析、运算求解的能力，属于基础题.‎ ‎7.设某大学的女生体重y（单位：kg）与身高x（单位：cm）具有线性相关关系，根据一组样本数据（xi，yi）（i=1，2，…，n），用最小二乘法建立的回归方程为=0.85x-85.71，则下列结论中不正确的是 A. y与x具有正的线性相关关系 B. 回归直线过样本点的中心（，）‎ C. 若该大学某女生身高增加‎1cm，则其体重约增加‎0.85kg D. 若该大学某女生身高为‎170cm，则可断定其体重必为‎58.79kg ‎【答案】D ‎【解析】‎ 根据y与x的线性回归方程为 y=0.85x﹣85.71，则 ‎=0.85＞0，y 与 x 具有正的线性相关关系，A正确；‎ 回归直线过样本点的中心（），B正确；‎ 该大学某女生身高增加 ‎1cm，预测其体重约增加 ‎0.85kg，C正确；‎ 该大学某女生身高为 ‎170cm，预测其体重约为0.85×170﹣85.71=‎58.79kg，D错误．‎ 故选D．‎ ‎8.从装有2个红球和2个黑球的口袋内任取两个球，那么互斥而不对立的事件是（ ）‎ A. 至少有一个黑球与都是黑球 B. 至少有一个黑球与至少有一个红球 C. 恰好有一个黑球与恰好有两个黑球 D. 至少有一个黑球与都是红球 ‎【答案】C ‎【解析】‎ ‎【分析】‎ 列举每个事件所包含的基本事件，结合互斥事件和对立事件的定义求解.‎ ‎【详解】A. “至少有一个黑球”等价于“一个黑球和一个红球或两个黑球”与“都是黑球”可以同时发生，不是互斥事件，故错误.‎ B. “至少有一个黑球” 等价于“一个黑球和一个红球或两个黑球”，“至少有一个红球”等价于“一个黑球和一个红球或两个红球”，可以同时发生，故错误.‎ C. “恰好有一个黑球” 等价于“一个黑球和一个红球”，与“恰好有两个黑球”，不同时发生，还有可能都是红球，不是对立事件，故正确.‎ D. “至少有一个黑球” 等价于“一个黑球和一个红球或两个黑球”，与“都是红球”，不同时发生，但一定会有一个发生，是对立事件，故错误.‎ 故选：C ‎【点睛】本题主要考查互斥事件与对立事件，还考查了理解辨析能力，属于基础题.‎ ‎9.已知向量，，与共线，则 （ ）‎ A. B. ‎2 ‎C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 根据与共线列方程，化简后求得的值.‎ ‎【详解】，，‎ 由于与共线，所以，所以.‎ 故选：C ‎【点睛】本小题主要考查平面向量共线的坐标表示，属于基础题.‎ ‎10.下图所示的茎叶图记录了甲、乙两组各5名工人某日的产量数据（单位：件）若这两组数据的中位数相等，且平均值也相等，则和的值分别为 A. 5，5 B. 3，‎5 ‎C. 3，7 D. 5，7‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 利用茎叶图、中位数、平均数的性质直接求解．‎ ‎【详解】由茎叶图得：‎ ‎∵甲、乙两组各5名工人某日的产量数据（单位：件）若这两组数据的中位数相等，‎ ‎∴65＝60+y，解得y＝5，‎ ‎∵平均值也相等，‎ ‎∴，‎ 解得x＝3．‎ 故选B．‎ ‎【点睛】本题考查实数值的求法，考查茎叶图、中位数、平均数的性质等基础知识，考查运算求解能力，是基础题．‎ ‎11.计算的结果为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 利用诱导公式、两角差的正弦公式进行化简求值.‎ ‎【详解】‎ ‎.‎ 故选：A ‎【点睛】本小题主要考查两角差的正弦公式、诱导公式，属于基础题.‎ ‎12.在正方形中，、分别是、的中点，若，则实数（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 将向量、用、表示，进而可将、用、表示，再由向量加法的平行四边形法则得出，代入可求得实数、的值，由此可得出的值.‎ ‎【详解】因为，①；‎ ‎，②‎ 由①②得，，‎ ‎，‎ 因为，所以，，.‎ 故选：C.‎ ‎【点睛】本题考查利用平面向量的基本定理求参数，解答的关键在于选择合适的基底表示向量，考查计算能力，属于中等题.‎ 二.填空题 ‎13.一个圆及其内接正三角形如图所示，某人随机地向该圆内扎针，则针扎到阴影区域的概率为________‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 利用面积型几何概型概率计算公式，计算出所求概率.‎ ‎【详解】设正三角形的边长为a，圆的半径为R，则由正弦定理得，所以正三角形的面积为，圆的面积.‎ 由几何概型的概率计算公式，得针扎到阴影区域的概率.‎ 故答案为：‎ ‎【点睛】本小题主要考查几何概型概率计算，属于基础题.‎ ‎14.计算：__________.‎ ‎【答案】4‎ ‎【解析】‎ ‎【详解】‎ ‎15.某服务电话，打进的电话响第一声时被接听的概率为0.1，响第二声时被接听的概率为0.2，响第三声时被接听的概率为0.3，响第四声时被接听的概率为0.35，则打进的电话响第五声前被接听的概率为________.‎ ‎【答案】0.95‎ ‎【解析】‎ ‎【分析】‎ 根据互斥事件概率求法即可得解.‎ ‎【详解】事件“响第一声时被接听”“响第二声时被接听”“响第三声时被接听”“响第四声时被接听”彼此互斥，‎ 所以“电话响第五声前被接听”的概率为.‎ 故答案为：0.95‎ ‎【点睛】本题考查了互斥事件概率的求法，属于基础题.‎ ‎16.已知，，且，，则________.‎ ‎【答案】‎ ‎【解析】‎ ‎【分析】‎ 根据同角三角函数关系式及已知条件，分别求得及， 由，利用正弦差角公式展开即可求得的值，再由即可得.‎ ‎【详解】因为，，且，，‎ 所以由同角三角函数关系式可得，‎ ‎，‎ 则 ‎，‎ 因为，‎ 所以.‎ 故答案为：.‎ ‎【点睛】本题考查了同角三角函数关系式的简单应用，正弦差角公式的展开式及应用，属于基础题.‎ 三.解答题 ‎17.某校在高二数学竞赛初赛考试后，对90分以上（含90分）的成绩进行统计，其频率分布直方图如图所示，若分数段的学生人数为2.‎ ‎（1）求该校成绩在分数段的学生人数；‎ ‎（2）估计90分以上（含90分）的学生成绩的众数、中位数和平均数（结果保留整数）.‎ ‎【答案】（1）40；（2）众数115、中位数113，平均数113.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）先求得成绩在内的频率，结合分数段的人数即可求得成绩在分数段的学生人数；‎ ‎（2）根据频率分布直方图中最高矩形，即可得众数；从左至右，将小矩形面积求和，至面积和为0.5时，对应底边的数值即为中位数；将各小矩形面积乘以对应底边的中点值，求和即为平均数的估计值.‎ ‎【详解】（1）∵分数段的频率为，‎ 又分数段的人数为2， ‎ ‎∴分数段的参赛学生人数为.‎ ‎（2）根据频率分布直方图，最高小矩形底面中点值为115，所以90分以上（含90分）的学生成绩的众数的估计值为115，‎ 从左依次计算各小矩形的面积为，因而中位数的估计值为，‎ 平均数的估计值为.‎ ‎【点睛】本题考查了频率分布直方图的简单应用，由频率分布直方图估计众数、中位数与平均数，属于基础题.‎ ‎18.（1）已知平面向量，的夹角为，且，，求与的夹角；‎ ‎（2）已知向量，求与向量垂直的单位向量的坐标.‎ ‎【答案】（1）；（2）或.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）根据平面向量数量积定义先求得，再由平面向量数量积运算律及模的求法求得，即可求得与夹角的余弦值，进而求得与的夹角.‎ ‎（2）设与向量垂直的单位向量的坐标为，根据单位向量模长及垂直向量的坐标关系，即可求得.‎ ‎【详解】（1）平面向量，的夹角为，且，，‎ 由平面向量数量积定义可知 ‎，‎ 因而 ‎，‎ 所以 ‎，‎ 由平面向量夹角的范围为，可知与的夹角为.‎ ‎（2）设与向量垂直的单位向量的坐标为，‎ 则，‎ 解方程组可得或，‎ 所以与向量垂直的单位向量的坐标为或.‎ ‎【点睛】本题考查了平面向量数量积定义，平面向量模的求法及向量夹角的求法，平面向量垂直的坐标关系应用，属于基础题.‎ ‎19. 某研究机构对高三学生的记忆力x和判断力y进行统计分析，得下表数据：‎ x ‎ ‎6 ‎ ‎8 ‎ ‎10 ‎ ‎12 ‎ y ‎ ‎2 ‎ ‎3 ‎ ‎5 ‎ ‎6 ‎ ‎（1）请在图中画出上表数据的散点图；‎ ‎（2）请根据上表提供的数据，用最小二乘法求出y关于x的线性回归方程；‎ ‎（3）试根据（2）求出的线性回归方程，预测记忆力为9的同学的判断力.‎ ‎【答案】（1）见图（2）＝0.7x－2.3（3）4.‎ ‎【解析】‎ 试题分析：（1）把所给的四对数据写成对应的点的坐标，在坐标系中描出来，得到散点图．‎ ‎（2）作出利用最小二乘法来求线性回归方程系数的量，求出横标和纵标的平均数，求出系数，再求出的值，注意运算不要出错．‎ ‎（3）由回归直线方程预测，记忆力为9的同学的判断力约为4．‎ 试题解析：(1）如图所示.‎ ‎(2)，‎ ‎，，，故线性回归方程为.‎ ‎（3）由回归直线方程，当x=9时，，故预测记忆力为9的同学的判断力约为4.‎ 考点：散点图,线性回归方程及其应用 ‎20.从一批草莓中，随机抽取个，其重量（单位：克）的频率分布表如下：‎ 分组（重量） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 频数（个） ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ ‎ 已知从个草莓中随机抽取一个，抽到重量在的草莓的概率为．‎ ‎（1）求出，的值；‎ ‎（2）用分层抽样的方法从重量在和的草莓中共抽取个，再从这个草莓中任取个，求重量在和中各有个的概率．‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）抽到重量在的草莓的概率为，，从而求出两个值；（2）古典概型的概率问题，关键是正确找出基本事件总数和所求事件包含的基本事件数，然后利用古典概型的概率计算公式计算；当基本事件总数较少时，用列举法把所有的基本事件一一列举出来，要做到不重不漏，有时可借助列表，树状图列举，利用古典概型的概率计算公式计算求值．‎ ‎【详解】（1）依题意可得，，从而得．‎ ‎（2）若采用分层抽样的方法从重量在和的草莓中共抽取5个，则重量在的个数为；记为，，‎ 在个数为；记为，，，‎ 从抽出的5个草莓中，任取个共有，，，，，，，，，10种情况．‎ 其中符合“重量在和中各有一个”的情况共有，，，，，6种．‎ 设事件表示“抽出的5个草莓中，任取个，重量在和中各有一个”，则．‎ 答：从抽出的5个草莓中，任取个，重量在和中各有一个的概率为．‎ 考点：1、频率分布表的应用；2、利用古典概型求随机事件的概率．‎ ‎21.（1）求的值. ‎ ‎（2）已知，，求值.‎ ‎【答案】（1）（2）‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用两角和正切公式进行化简求值.‎ ‎（2）利用平方的方法，求得的值，进而求得，从而求得的值..‎ ‎【详解】（1）由于，‎ 所以，‎ 所以.‎ ‎（2）由①两边平方并化简得，由于，所以，‎ 所以②.‎ 由①②得.‎ 所以 ‎.‎ ‎【点睛】本小题主要考查两角和的正切公式，考查两角差的正弦公式、二倍角公式，属于中档题.‎ ‎22.已知函数，其最小正周期为.‎ ‎（1）求的表达式；‎ ‎（2）将函数的图象向右平移个单位长度后，再将得到的图象上各点的横坐标伸长到原来的倍（纵坐标不变），得到函数的图象，若关于的方程在区间上有且只有一个实数解，求实数的取值范围.‎ ‎【答案】（1）；（2）.‎ ‎【解析】‎ ‎【分析】‎ ‎（1）利用三角恒等变换思想化简函数的解析式为，利用函数的最小正周期可求得的值，由此可得出函数的解析式；‎ ‎（2）利用三角函数图象变换可得，由可计算出的取值范围，由可得，可得出直线与函数在区间上的图象有且只有一个交点，数形结合可求得实数的取值范围.‎ ‎【详解】（1）‎ ‎，‎ 又因为函数最小正周期，所以，所以，‎ 所以；‎ ‎（2）将函数的图象向右平移个单位长度后，得到的图象.再将所得图象上所有点的横坐标伸长到原来的倍（纵坐标不变），得到的图象，所以，‎ 当时，，‎ 令，可得，令，可知直线与函数在区间上的图象有且只有一个交点，如下图所示：‎ 由图象可知，当或时，‎ 直线与函数在区间上的图象有且只有一个交点.‎ 所以实数的取值范围是.‎ ‎【点睛】本题考查利用三角恒等变换化简函数解析式，同时也考查了利用函数图象变换求函数解析式，以及利用正弦型函数的图象求解函数的零点个数问题，考查计算能力，属于中等题.‎