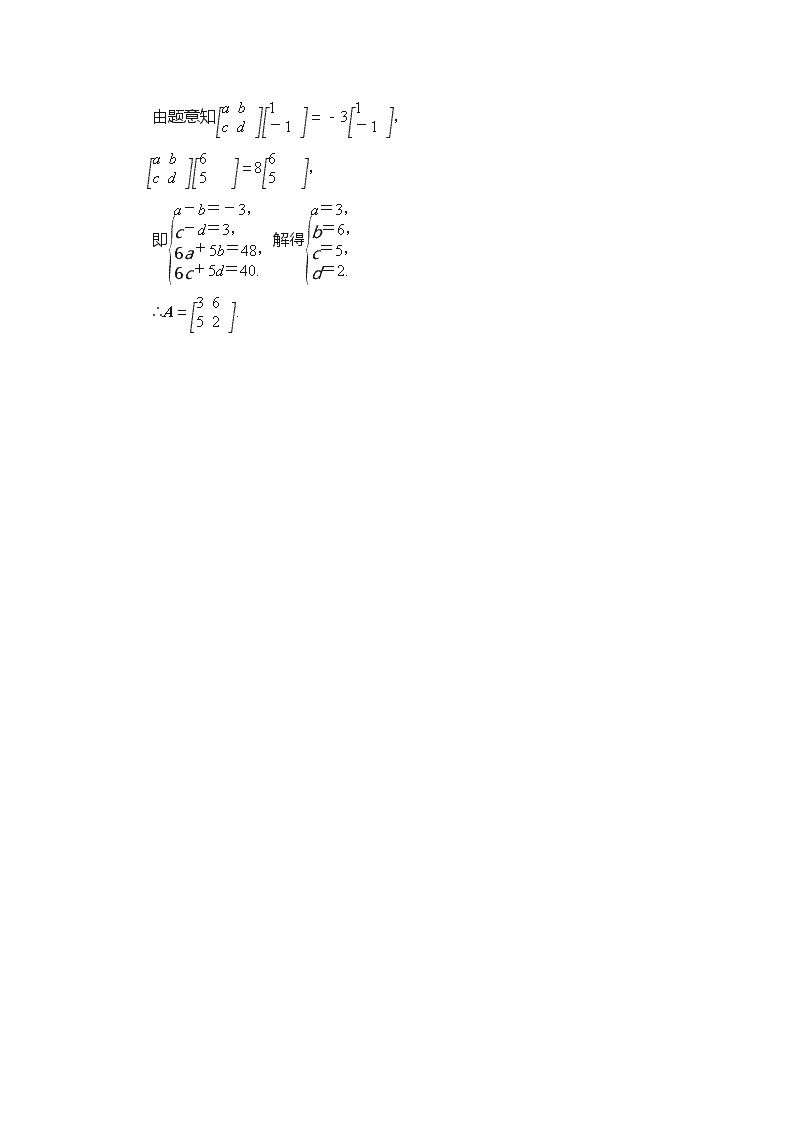【数学】2019届一轮复习苏教版矩阵的特征值与特征向量学案 3页

‎2019届一轮复习苏教版 矩阵的特征值与特征向量 学案 一、矩阵的特征值与特征向量的求解与应用 设A＝是一个二阶矩阵，λ是矩阵A的一个特征值，α是属于λ的一个特征向量.欲求λ及α，可令A的特征多项式等于0，即可求出λ的值，将λ的值代入方程组得到一组非零解，即为矩阵A的属于特征值λ的一个特征向量.‎ ‎　求矩阵M＝的特征值及其对应的特征向量.‎ ‎【解】　矩阵M的特征多项式为 f(λ)＝＝(λ－1)(λ－1)－4＝λ2－2λ－3.‎ 令f(λ)＝0，得矩阵M的特征值为－1和3.‎ 当λ＝－1时，联立，解得x＋y＝0‎ 所以矩阵M的属于特征值－1的一个特征向量为.‎ 当λ＝3时，联立，解得x＝y 所以矩阵M的属于特征值3的一个特征向量为.‎ 二、Anα的表示(计算)‎ 设λ1，λ2是二阶矩阵M的两个不同特征值，矩阵M的属于特征值λ1，λ2的特征向量分别为α1，α2，则平面上任一非零向量β可表示为β＝s α1＋t α2(其中s，t为实数)，则Mnβ＝Mn(s α1＋t α2)＝sλα1＋tλα2(n∈N*).‎ ‎　若矩阵A有特征值λ1＝2，λ2＝－1，它们所对应的特征向量分别为α1＝，α2＝.‎ ‎(1)求矩阵A和其逆矩阵A－1；‎ ‎(2)已知α＝，试求A100α.‎ ‎【解】　(1)设矩阵A＝，其特征多项式为f(λ)＝.‎ ‎∵当λ1＝2时，其特征向量为α1＝，‎ ‎∴∴ 同理当λ2＝－1时，其特征向量为α2＝，‎ ‎∴∴ ‎∴A＝，det(A)＝－2，‎ ‎∴A－1＝－＝.‎ ‎(2)设α＝s α1＋t α2，‎ 则＝s＋t，‎ ‎∴s＝1，t＝16.‎ ‎∴A100α＝1×2100×＋16×(－1)100× ‎＝＋＝.‎ 三、函数方程思想的应用 本章不论是由矩阵求特征值，还是已知矩阵的特征值与特征向量求该矩阵，都需要解方程(组)或构建方程(组)求解.‎ ‎　已知二阶矩阵A的属于特征值－3的一个特征向量为，属于特征值8的一个特征向量为，求矩阵A. ‎ ‎【导学号：30650054】‎ ‎【解】　设A＝，‎ 由题意知＝－3，‎ ＝8，‎ 即解得 ‎∴A＝.‎