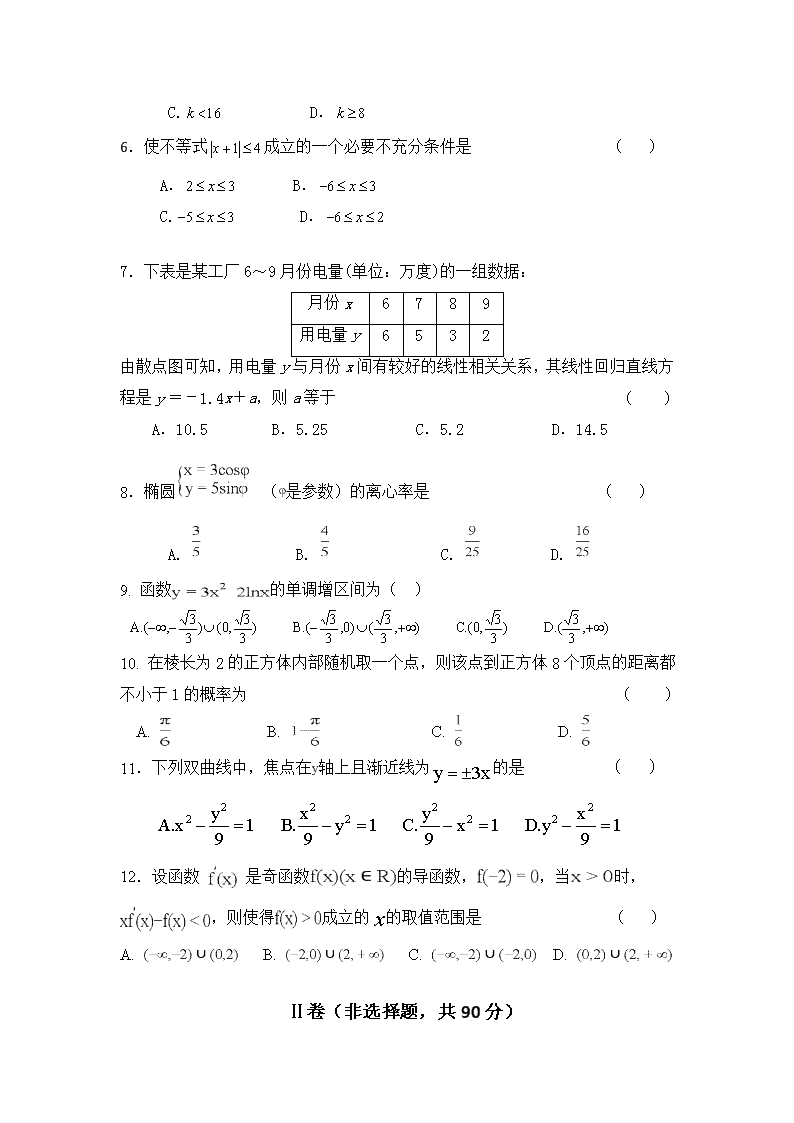- 792.00 KB
- 2021-04-25 发布
集宁一中2017-2018学年第二学期第一次月考
高二年级文科数学试题
本试卷分为Ⅰ卷(选择题)和Ⅱ卷(非选择题)两部分,共150分,考试时间120分钟。
Ⅰ卷(选择题,共60分)
一、选择题(每题5分,共60分。每小题只有一个选项符合题意)
1.复数z=的共轭复数是 ( )
A.2+i B.2-I C.-1+i D.-1-i
2. 以下有关命题的说法错误的是 ( )
A. 命题“若,则”的逆否命题是“若,则”
B. 命题“若或,则”的否命题为真命题
C. 若为假命题,则均为假命题
D. 对于命题,使得,则,均有
3.参数方程(t为参数)所表示的曲线是 ( )
4.已知是2,8的等比中项,则圆锥曲线的离心率是 ( )
A. 或 B. C. D. 或
5. 按照如图所示的程序框图执行,若输出的结果为,则处的条件为( )
A. B.
C. D.
6.使不等式成立的一个必要不充分条件是 ( )
A. B.
C. D.
7.下表是某工厂6~9月份电量(单位:万度)的一组数据:
月份x
6
7
8
9
用电量y
6
5
3
2
由散点图可知,用电量y与月份x间有较好的线性相关关系,其线性回归直线方程是=-1.4x+a,则a等于 ( )
A.10.5 B.5.25 C.5.2 D.14.5
8. 椭圆(是参数)的离心率是 ( )
A. B. C. D.
9. 函数的单调增区间为( )
10. 在棱长为2的正方体内部随机取一个点,则该点到正方体8个顶点的距离都不小于1的概率为 ( )
A. B. C. D.
11.下列双曲线中,焦点在轴上且渐近线为的是 ( )
12.设函数 是奇函数的导函数,,当时,,则使得成立的的取值范围是 ( )
A. B. C. D.
Ⅱ卷(非选择题,共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13. 已知函数 ,则 __________.
14.两条直线ρcos=2和tan θ=1的夹角为__________ .
15. 下列关于K2的说法中,正确的有________.
①K2的值越大,两个分类变量的相关性越大;
②K2的计算公式是K2=;
③若求出K2=4>3.841,则有95%的把握认为两个分类变量有关系,即有5%的可能性使得“两个分类变量有关系”的推断出现错误;
④独立性检验就是选取一个假设H0条件下的小概率事件,若在一次试验中该事件发生了,这是与实际推断相抵触的 “不合理”现象,则作出拒绝H0的推断.
16.过点作抛物线的弦,恰被所平分,则弦所在直线方程为______.
三、解答题(共6个题,共70分,解答应写出文字说明,证明过程
或演算步骤)
17.(本题满分10分)
求直线(t为参数)被曲线ρ=cos所截的弦长.
18.(本题满分12分) 已知命题p:k2﹣8k﹣20≤0,命题q:方程=1表示焦点在x轴上的双曲线.
(1)命题q为真命题,求实数k的取值范围;
(2)若命题“p∨q”为真,命题“p∧q”为假,求实数k的取值范围.
19.(本题满分12分) 已知函数, (为自然对数的底数).
(1)若是的极值点,求实数的值;
(2)求的单调递增区间.
20.(本小题满分12分) 某高校在年的自主招生考试成绩中随机抽取名学生的笔试成绩,按成绩分组:第组,第组,第组,第组,第组得到的频率分布直方图如图所示.
(1)分别求第,,组的频率;
(2)若该校决定在笔试成绩高的第,,组中用分层抽样抽取名学生进入第二轮面试,求第,,组每组各抽取多少名学生进入第二轮面试?
(3)在(2)的前提下,学校决定在这名学生中随机抽取名学生接受甲考官的面试,求第组至少有一名学生被甲考官面试的概率.
21.(本题满分12分) 已知椭圆(a>b>0)的离心率是,其左、右焦点分别为F1,F2,短轴顶点分别为A,B,如图所示,△ABF2的面积为1.
(1)求椭圆C的标准方程;
(2)过点P(﹣1,1)且斜率为k的直线l交椭圆C于M,N两点(异于A,B点),证明:直线BM和BN的斜率和为定值.
22.(本小题满分12分)已知函数, (为常数).
(1)若函数与函数在处有相同的切线,求实数的值.
(2)若,且,证明: .
高二文科数学答案
一.选择题 DCDDA BDBDB CA
二.非选择题
13. —2 14. 90° 15. ③④ 16.
17.解: 将方程ρ=cos分别化为普通方程3x+4y+1=0,x2+y2-x+y=0,圆心C,半径为,圆心到直线的距离d=,弦长=2=2=.
18.解:(Ⅰ)当命题q为真时,由已知得,解得1<k<4
∴当命题q为真命题时,实数k的取值范围是1<k<4
(Ⅱ)当命题p为真时,由k2﹣8k﹣20≤0解得﹣2≤k≤10
由题意得命题p、q中有一真命题、有一假命题
当命题p为真、命题q为假时,则,
解得﹣2≤k≤1或4≤k≤10.
当命题p为假、命题q为真时,则,k无解.
∴实数k的取值范围是﹣2≤k≤1或4≤k≤10.
19.解: (Ⅰ)
由,得,此时是的极小值点.
(Ⅱ)由,得或.
①当时, , 的单调递增区间是;
②当时, , 的单调递增区间是;
③当时, , 的单调递增区间是.
20. 解:(1)由题设可知,第组的频率为;
第组的频率为
第组的频率为
(2)第三组人;第四组的人数为人;
第五组的人数为人;
因为第,,组共有名学生,所以利用分层抽样在名学生中抽取名学生,每组抽取的人数分别为:
第组抽人;第组抽人;第组抽人;
所以第,,组分别抽取出人,人和人.
(3)设第组的位同学为,,,第组的两位同学为,,第组的位同学为,
则从六位同学中抽两位同学有:,,,,,,,,,,,,,,共种可能.
其中第组的两位同学为,,至少有一位同学入选的有:,,,,,,,,,,
共种可能.
所以第组至少有一学生被甲考官面试的概率为
21. 解:(1),a2=2c2,b2=c2,又bc=1,∴
所以椭圆的标准方程为
(2)证明:设直线l的方程为y=k(x+1)+1,M(x1,y1),N(x2,y2)
联立得(2k2+1)x2+4k(k+1)x+2k2+4k=0,[]
∴,
∴
=.
=.
∴直线BM与BN的斜率之和为定值.
22. 解:(1), ,
因为在处有相同的切线,所以,则,即.
(2)若,则,设,
则, ,
,因为,所以,即单调递减,
又因为,所以,即单调递减,
而,所以,即.