- 2.03 MB
- 2021-04-25 发布
2017-2018 学年内蒙古赤峰二中高二 4 月月考
理科数学试题
一、选择题:本大题共 12 小题,每小题 5 分,共 60 分,在每小题给出的四个选项中,只有一项是
符合题目要求的.
1.已知复数 z= 10
3+i
-2i (其中 i 为虚数单位),则|z|=
A.3 3 B.3 2 C.2 3 D.2 2
2.设集合 A={(x,y)|x2+y2=1},B={(x,y)|y=3x},则 A∩B 的子集的个数是
A.4 B.3 C.2 D.1
3.为了研究某班学生的脚长 x(单位:厘米)和身高 y (单位:厘米)的关系,从该班随机抽
取 10 名学生,根据测量数据的散点图可以看出 y 与 x 之间有线性相关关系,设其回归直线方
程为 ˆˆ ˆy bx a .已知
10
1
225i
i
x
,
10
1
1600i
i
y
, ˆ 4b .该班某学生的脚长为 24,据此
估计其身高为
A 160 B 163 C 166 D 170 [
4.我国古代数学名著《九章算术》有“米谷粒分”题:粮仓开仓收粮,有人送来米 1534 石,验
得米内夹谷,抽样取米一把,数得 254 粒内夹谷 28 粒,则这批米内夹谷约为( )
A.134 石 B.169 石 C.338 石 D.1365 石
5. 某 校 从 高 一 年 级 学 生 中 随 机 抽 取 部 分 学 生 , 将 他 们 的 模 块 测 试 成 绩 分 成 6 组 :
[40,50),[50,60),[60,70),[70,80),[80,90),[90,100]加以统计,得到如图所示的频率分布直方图.已知
高一年级共有学生 600 名,据此估计,该模块测试成绩不少于 60 分的学生人数为( ).
A.588 B.480 C.450 D.120
6.已知 1 是 lga 与 lgb 的等比中项,若 a>1,b>1,则 ab 有( )
A.最小值 10 B.最大值 100 C.最大值 10 D.最小值 100
7.设函数 f(x)=sin(ωx+φ)+cos(ωx+φ) 的最小正周期为π,且 f
(﹣x)=f(x),则
A . f(x)在 单调递减 B. f(x)在( , )单调递减
C. f(x)在(0, )单调递增 D . f(x)在( , )单调递增
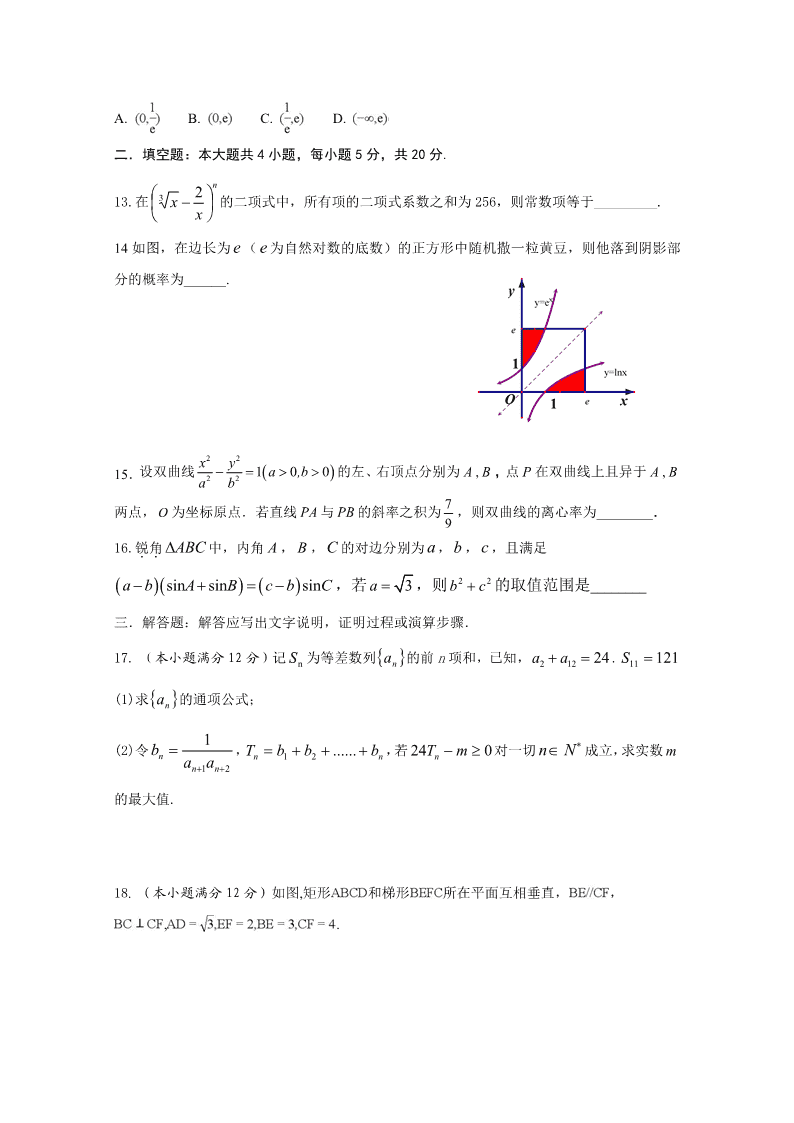
8.如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”.执
行该程序框图,若输入的 a,b 分别为 72,27,则输出的 a
A.18 B.9 C.6 D.3
9.某校校庆期间,大会秘书团计划从包括甲、乙两人在内的七名老师中随机选择 4 名参加志
愿者服务工作,根据工作特点要求甲、乙两人中至少有 1 人参加,则甲、乙都被选中且列队
服务时不相邻的概率为
A. 1
2
B. 1
3
C. 1
6
D. 1
4
10 圆柱被一个平面截去一部分后与半球(半径为 r)组成一个几何体,该几何体三视图中的正视
图和俯视图如图所示.若该几何体的表面积为 16 + 20 ,则 r=()
A 1 B 8 C 4 D 2
11. 抛物线 xy 122 的焦点为 F,抛物线的弦 AB 经过焦点 F,以 AB 为直径的圆与直线
)0( ttx 相切于 )6,( tM ,则线段 AB 的长为( )
A.12 B. 18 C. 16 D. 24
12. 已知函数 (为自然对数的底数)有两个极值点,则实数的取值范围是( )
A. B. C. D.
二.填空题:本大题共 4 小题,每小题 5 分,共 20 分.
13.在
n
xx
23 的二项式中,所有项的二项式系数之和为 256,则常数项等于_________.
14 如图,在边长为 e ( e 为自然对数的底数)的正方形中随机撒一粒黄豆,则他落到阴影部
分的概率为______.
15.设双曲线
2 2
2 2 1 0 0x y a ,ba b
的左、右顶点分别为 A , B ,点 P 在双曲线上且异于 A , B
两点, O 为坐标原点.若直线 PA 与 PB 的斜率之积为 7
9
,则双曲线的离心率为________.
16.锐角.. ABC 中,内角 A , B ,C 的对边分别为 a ,b , c ,且满足
sin sin sina b A B c b C ,若 3a ,则 2 2b c 的取值范围是________
三.解答题:解答应写出文字说明,证明过程或演算步骤.
17. (本小题满分 12 分)记 nS 为等差数列 na 的前 n 项和,已知, 24122 aa . 12111 S
(1)求 na 的通项公式;
(2)令
21
1
nn
n aab , nn bbbT ......21 ,若 024 mTn 对一切 Nn 成立,求实数 m
的最大值.
18. (本小题满分 12 分)如图,矩形 和梯形 所在平面互相垂直, ,
, .
(Ⅰ)求证: 平面 ;
(Ⅱ)当 的长为何值时,二面角 的大小为 60°.
19. (本小题满分 12 分)一盒中装有 9张各写有一个数字的卡片,其中 4 张卡片上的数字是1,
3张卡片上的数字是 2 , 2 张卡片上的数字是 3 .从盒中任取3 张卡片.
(1)求所取 3 张卡片上的数字完全相同的概率
(2) X 表示所取 3 张卡片上的数字的中位数,求 X 的分布列与数学期望.
20.(本小题满分 12 分)椭圆 )0(1: 2
2
2
2
ba
b
y
a
xC 的中心在原点,焦点在 x 轴上,焦
距为 2 ,且与椭圆 12
2
2 yx 有相同离心率.
(1)求椭圆C 的方程;
(2)若直线 mkxyl : 与椭圆C 交于不同的 BA, 两点,且椭圆C 上存在点Q ,满足
OQOBOA ,(O 为坐标原点),求实数 取值范围.
21.(本小题满分 12 分)已知函数 xaxxf ln)1()( 2
(1)若曲线 )(xfy 在 )1(,1 f 处的切线与直线 012 yx 垂直,求 a 的值;并判断此时
)(xf 的单调性;
(2)若 )(xf 有两个极值点 21, xx ,且 21 xx ,当 1)( 21 mxxf 恒成立时,求 m 的取值范
围。
请考生在第 22、23 两题中任选一题作答.注意:只能做所选定的题目.如果多做,则按所做的
第一个题目计分.
22.(本小题满分 10 分) 选修 4-4:坐标系与参数方程
在直角坐标系 xOy 中,曲线 C1 的参数方程为 x=2+2cosα,
y=2sinα
(α为参数),曲线 C2 的参数
方程为 x=2cosβ,
y=2+2sinβ
(β为参数),以 O 为极点,x 轴的正半轴为极轴建立极坐标系.
(1)求曲线 C1 和曲线 C2 的极坐标方程;
(2)已知射线 l1:θ=α(0<α<π
2),将射线 l1 顺时针旋转π
6
得到射线 l2:θ=α-π
6
,且射线 l1 与
曲线 C1 交于 O,P 两点,射线 l2 与曲线 C2 交于 O,Q 两点,求|OP|·|OQ|的最大值.
23.(本小题满分 10 分)选修 4—5;不等式选讲
已知函数 2( ) | 2 |f x x a .
(Ⅰ)若 3| |(0) (1) af f a
,求实数 a 的取值范围;
(Ⅱ)对任意| | 1 ( ) 1x f x≤ , ≤ 恒成立,求实数 a 的值.
理科数学答案
选择题 1---12 BACBB DABCD DA
12【答案】A
【解析】 ,
若函数 有两个极值点,
则 和 在 有 2 个交点,
令 , 则 ,
在 递减 , 而 ,
故 时 , , 即 , 递增,
时 , , 即 , 递减,
故 ,
而 时 , , 时 , ,
若 和 在 有 2 个交点
只需 ,
13【答案】 14【答案】 15. 16 答案.
17. (12 分)解:(1)∵等差数列 中, , .
∴ ,解得 . ……………………………2 分
,……………………………3 分
. ……………………………5 分
(2) ……………………………7 分
,………9 分
是递增数列, ,
,
∴实数 的最大值为 .……………………………12 分
18(1)证明:在 中, , , , ,
所以 .又因为在 中, ,所以 .
由已知条件知, 平面 ,所以 .
又 ,所以 平面
(2)如图,以点 C 为坐标原点,以 CB,CF 和 CD 分别作为 x 轴,y 轴和 z 轴,建立空间直
角坐标系 C-xyz.
设 AB=a(a >0),则 C(0,0,0),A( ,0,a),B( ,0,0),E( , 3,0),F(0,4,0).从
而
设平面 AEF 的法向量为 ,由 得,
取 x=1,则 ,即 .
不妨设平面 EFCB 的法向量为 ,
由条件,得 ,
解得 .所以当 时,二面角 A-EF-C 的大小为 60°.
18 解:(1)由古典概型中的概率计算公式知所求概率为
(2) 的所有可能值为 1,2,3,且
, ,
,故 的分布列为:
1 2 3
从而
20.解:(1)由已知可 解得 .……………3 分
所求椭圆 的方程 . ………4 分
(2)建立方程组 消去 ,整理得 .
.
由于直线直线 与椭圆 交于不同的 两点,
,有 .① ………………6 分
设 ,于是 ,
. ………8 分
当 时,易知点 关于原点对称,则 ;
当 时,易知点 不关于原点对称,则 .
此时,
由 ,得 即
点在椭圆上,∴ .
化简得 . .②
由①②两式可得 .
综上可得实数 的取值范围是 . …12 分
21 解: ,所
以在 为增函数。
(2)
令
所以, 为减函数,所以
22.(1)曲线 C1 的直角坐标方程为(x-2)2+y2=4 1 分所以 C1 的极
坐标方程为ρ=4cosθ 2 分
曲线 C2 的直角坐标方程为 x2+(y-2)2=4, 3 分
所以 C2 的极坐标方程为ρ=4sinθ. 4 分
(2)设 P 的极坐标为(ρ1,α), 5 分
即ρ1=4cosα,点 Q 的极坐标为(ρ2,(α-
π
6 )),即ρ2=4sin(α-
π
6 ), 6 分
则|OP|·|OQ|=ρ1ρ2=4cosα·4sin(α-
π
6 )=16cosα·(
3
2sinα-
1
2cosα)
=8sin(2α-
π
6 )-4.∵α∈(0,
π
2 ), 8 分∴2α-
π
6 ∈(-
π
6 ,
5π
6 ).当 2α-
π
6 =
π
2 ,即α
=
π
3 时,|OP|·|OQ|取最大值 4. 10
(23)(本小题满分 10 分)选修 4-5:不等式选讲
解析:(Ⅰ)当 时, 可转化为 ,该不等式恒成立;
当 时, 可转化为 .
综上可得,实数 的取值范围是
…5 分
(Ⅱ)对任意 恒成立,可得 ,即 ,①
又 ,即 ,② 由①②可知 .验证 时 恒成立.
…10 分