- 1.28 MB
- 2021-04-25 发布
九江一中2017-2018学年高二开学考试数学试题(文)
一、选择题(每题5分,共60分)
1.若函数是幂函数,则的值为( )
A. B. C. D.
2.若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是________.
A.8 B.7 C.6 D.5
3.已知直线与平行,则实数a的取值是( )
A.-1或2 B.0或1 C.-1 D.2
4.某校高三(1)班共有48人,学号依次为1,2,3,…,48,现用系统抽样的办法抽取一个容量为6的样本.已知学号为3,11,19,35,43的同学在样本中,那么还有一个同学的学号应为( )
A.27 B.26 C.25 D.24
5.已知函数,那么的值为
A. B. C. D.
6.从集合中随机抽取一个数,从集合中随机抽取一个数,则向量与向量垂直的概率为
A. B. C. D.
7.在内,使成立的取值范围为( )
A. B. C. D.
8.直线R与圆的交点个数是( )
A. 0 B. 1 C. 2 D.无数个
9.已知在长方体ABCDA1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A . B. C. D.
10.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )
A. B.
C. D.
11.函数,,在上的部分图象如图所示,则的值为( ).
A. B. C. D.
12. 已知实数若关于的方程有三个不同的实根,则的取值范围为( )
A. B. C. D.
二、填空题(每题5分,共20分)
13.点在映射下得对应元素为,则在作用下点的原象是
14.若,则______
15.已知的定义域是[1,2],则的定义域是 .
16.若向量,且则的最小值为 _______
三、解答题(共70分)
17.(本题满分10分)已知函数,
(1)求函数的最小正周期与单调递增区间;
(2)若时,函数的最大值为0,求实数的值.
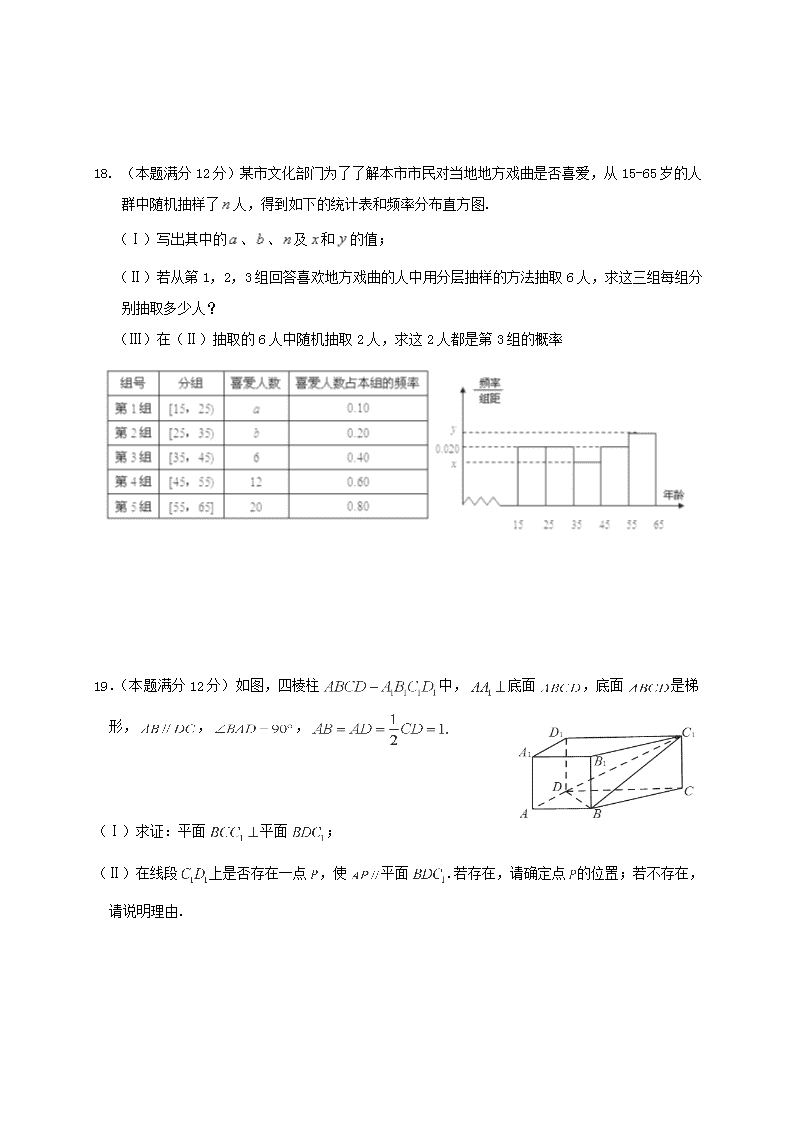
18. (本题满分12分)某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了人,得到如下的统计表和频率分布直方图.
(Ⅰ)写出其中的、、及和的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求这2人都是第3组的概率
19.(本题满分12分)如图,四棱柱中,底面,底面是梯形,,,
(Ⅰ)求证:平面平面;
(Ⅱ)在线段上是否存在一点,使平面.若存在,请确定点的位置;若不存在,请说明理由.
20.(本题满分12分)已知满足,若其图像向左平移个单位后得到的函数为奇函数.
(1)求的解析式;
(2)在锐角中,角的对边分别为,且满足,求的取值范围.
21. (本题满分12分)已知函数.
(1)若函数在上至少有一个零点,求的取值范围;
(2)若函数在上的最大值为3,求的值.
22.(本小题12分)如图,在平面直角坐标系中,已知以为圆心的圆及其上一点
(1)设圆与轴相切,与圆外切,且圆心在直线上,求圆的标准方程;
(2)设平行于的直线与圆相交于两点,且,求直线的方程;
九江一中2019届高二开学考试
数学试题(文)答案
一、选择题
1A2B3C4A56A7C8C9C10D11B12
1.若函数是幂函数,则的值为( )
A. B. C. D.
1.A
【解析】函数是幂函数,则即。
2.若某程序框图如图所示,当输入50时,则该程序运行后输出的结果是________.
3.已知直线与平行,则实数a的取值是( )
A.-1或2 B.0或1 C.-1 D.2
4.某校高三(1)班共有48人,学号依次为1,2,3,…,48,现用系统抽样的办法抽取一个容量为6的样本.已知学号为3,11,19,35,43的同学在样本中,那么还有一个同学的学号应为( )
A.27 B.26 C.25 D.24
4.A
【解析】
试题分析:根据系统抽样的规则——“等距离”抽取,也就抽取的号码差相等,根据抽出的序号可知学号之间的差为,所以在与之间还有,故选A.
5.已知函数,那么的值为
A. B. C. D.
6.从集合中随机抽取一个数,从集合中随机抽取一个数,则向量与向量垂直的概率为
(A) (B) (C) (D)
6.A
【解析】
试题分析:由题意可知有:.共个.
即所以即,有,共个满足条件.
故所求概率为.
7.在内,使成立的取值范围为( )
A. B. C. D.
7.C
【解析】
试题分析:∵sinx>cosx,∴sin(x-)>0,∴2kπ<x-<2kπ+π (k∈Z),∵在(0,2π)内,∴x∈(,),故选D.
8.直线R与圆的交点个数是( )
A. 0 B. 1 C. 2 D.无数个
8.C
【解析】
试题分析:判断直线与圆的位置关系经常利用圆的几何性质来解决,即当圆心到直线的距离小于半径时,直线与圆相交,故本题应先求圆心(2,0)到直线x+ay-1=0的距离,再证明此距离小于半径,即可判断交点个数。解:圆的圆心O(2,0),半径为2,圆心O到直线 R的距离为d=∴a2+1≥1,∴d≤1<2,即圆心到直线的距离小于半径,,∴直线 R与圆的交点个数是2,故选C
9.已知在长方体ABCDA1B1C1D1中,底面是边长为2的正方形,高为4,则点A1到截面AB1D1的距离是( )
A . B. C. D.
9.C
【解析】点A1到截面AB1D1的距离是,
由可得 解得
10.一个几何体的三视图如图所示,且其侧视图是一个等边三角形,则这个几何体的体积为( )
A. B.
C. D.
10.D
【解析】
试题分析:由题设中的三视图可得,该几何体是有一个半圆锥和一个四棱锥的组合而成的组合体,其中半圆锥的底面半径为,四棱锥的底面是一个边长为的正方形,它们的高均为,则几何体的体积为,故选D.
11.函数,,在上的部分图象如图所示,则的值为 .
【解析】
试题分析:根据题意,由于函数,,在上的部分图象可知周期为12,由此可知,A=5,将(5,0)代入可知,5sin(+)=0,可知=,故可知==,故答案为
12. 已知实数若关于的方程有三个不同的实根,则
的取值范围为( )A. B. C. D.
13.点在映射下得对应元素为,则在作用下点的原象是
14.若,则______
15.已知的定义域是[1,2],则的定义域是 .
16.若向量,且则的最小值为 _______
16.
17.已知函数,
(1)求函数的最小正周期与单调递增区间;
(2)若时,函数的最大值为0,求实数的值.
17.(1),单调递增区间为,;(2).
【解析】
试题分析:(1)化简,求出在最小正周期,解不等式,求出函数的递增区间即可;(2)根据的范围,求出的范围,得到关于的方程,解出即可.
试题解析:(1)
则函数的最小正周期,
根据,得,
所以函数的单调递增区间为,.
(2)因为,所以,
则当,时,函数取得最大值0,
即,解得:.
18. (本题满分12分)某市文化部门为了了解本市市民对当地地方戏曲是否喜爱,从15-65岁的人群中随机抽样了人,得到如下的统计表和频率分布直方图.
(Ⅰ)写出其中的、、及和的值;
(Ⅱ)若从第1,2,3组回答喜欢地方戏曲的人中用分层抽样的方法抽取6人,求这三组每组分别抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求这2人都是第3组的概率
18.解:(Ⅰ)由表可知第3组,第4组 的人数分别为,,再根据直方图可知第1组、第2组的 人数也为人,且抽样总人数.
所以第5组的人数为,且 ,,,,. ………… 4分
(Ⅱ)因为第1,2,3组喜欢地方戏曲的人数比为,那么用分层抽样的方法从这三组中抽取6人,第1组应抽取1人,第2组应抽取2人,第3组应抽取3人. (Ⅲ),,
19.(本题满分12分)如图,四棱柱中,底面,底面是梯形,,,
(Ⅰ)求证:平面平面;
(Ⅱ)在线段上是否存在一点,使平面.若存在,请确定点的位置;若不存在,请说明理由.
19.【解析】
试题解析:(Ⅰ)因为底面, 所以底面,因为底面,
所以因为底面是梯形,,,
因为,所以,所以,
所以在中,所以所以
又因为所以平面因为平面,所以平面平面
(Ⅱ)存在点是的中点,使平面
证明如下:取线段的中点为点,连结,所以,且因为,所以,且所以四边形是平行四边形.所以
又因为平面,平面,所以平面
20.(本题满分12分)已知满足,若其图像向左平移个单位后得到的函数为奇函数.
(1)求的解析式;
(2)在锐角中,角的对边分别为,且满足,求的取值范围.
20.(1);(2).
【解析】试题解析:(1)∵,∴,
∴,∴,则的图象向左平移个单位后得到的函数为
,而为奇函数,则有, ,而,
则有,从而.(2),
由正弦定理得: ,∵,∴,
∴,∴∵是锐角三角形, ,
∴,∴,∴,∴.
21.已知函数.
(1)若函数在上至少有一个零点,求的取值范围;
(2)若函数在上的最大值为3,求的值.
【答案】(1);(2)或.
22(本题满分12分)如图,在平面直角坐标系中,已知以为圆心的圆及其上一点
(1)设圆与轴相切,与圆外切,且圆心在直线上,求圆的标准方程;
(2)设平行于的直线与圆相交于两点,且,求直线的方程;
【答案】(1)(2)(3)
(3)设
因为,所以 ……①
因为点Q在圆M上,所以 …….②
将①代入②,得.
于是点既在圆M上,又在圆上,
从而圆与圆有公共点,
所以 解得.
因此,实数t的取值范围是.