西藏自治区日喀则市南木林高级中学2019-2020学年高一第二学期期中考试数学试卷 6页

西藏自治区日喀则市南木林高级中学2019-2020学年 高一第二学期期中考试数学试卷 注意事项：‎ ‎1、本试题全部为笔答题，共6页，满分100分，考试时间90分钟。‎ ‎2、答卷前将密封线内的项目填写清楚，密封线内禁止答题。‎ ‎3、用钢笔或签字笔直接答在试卷(或答题纸上)。‎ ‎4、本试题为闭卷考试，请考生勿将课本进入考场。‎ 一、 选择题：本大题共12小题，每小题4分，共48分．每小题给出的四个选项中，只有一项是符合要求的．‎ ‎ 1. 从学号为0～50的高一某班50名学生中随机选取5名同学参加数学测试,采用系统抽样的方法,则所选5名学生的学号可能是( )‎ ‎ A. 1,2,3,4,5 B. 5,16,27,38,49 C. 2,4,6,8,10 D. 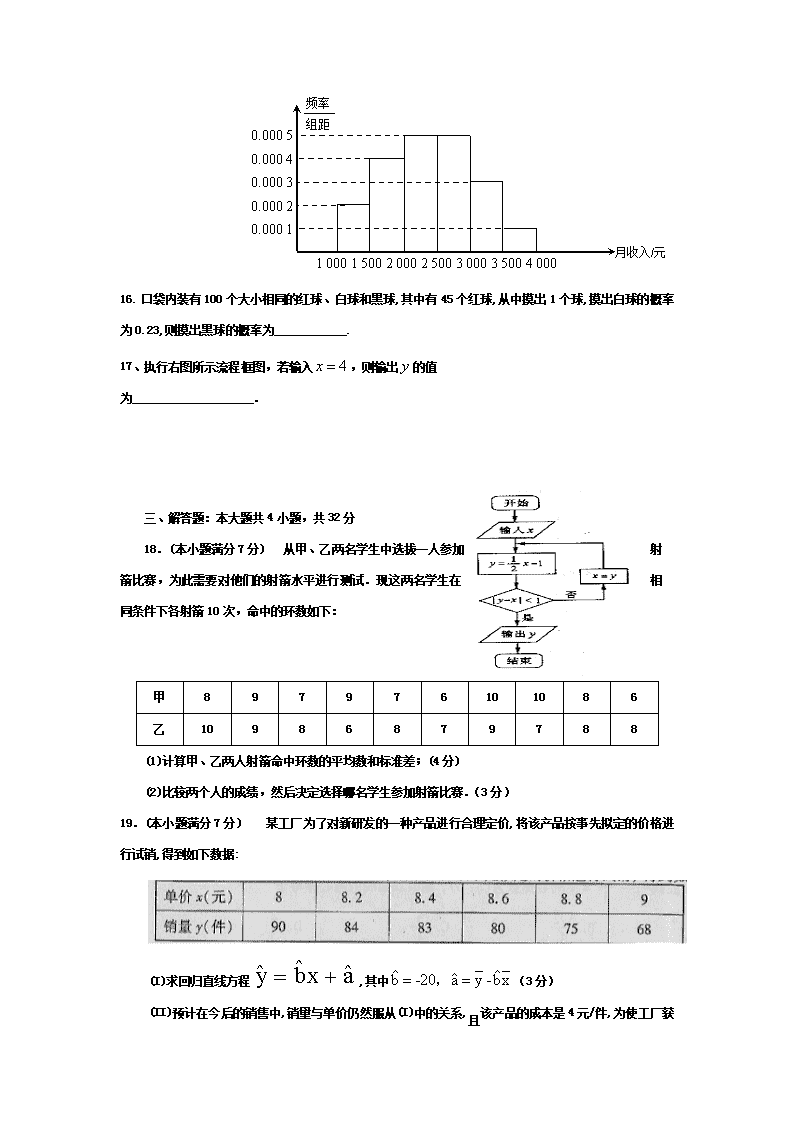4,13,22,31,40、‎ ‎ 2．一个容量为1 000的样本分成若干组，已知某组的频率为0.4，则该组的频数是( ).‎ A．400 B．40 C．4 D．600‎ ‎3．从1，2，3，4这4个数中，不放回地任意取两个数，两个数都是奇数的概率是( ).‎ A． B． C． D．‎ ‎4．通过随机抽样用样本估计总体，下列说法正确的是( ).‎ A．样本的结果就是总体的结果 B．样本容量越大，可能估计就越精确 C．样本的标准差可以近似地反映总体的平均状态 D．数据的方差越大，说明数据越稳定 ‎5．把11化为二进制数为( ).‎ A．1 011(2) B．11 011(2) C．10 110(2) D．0 110(2)‎ ‎6．已知x可以在区间[－t，4t](t＞0)上任意取值，则x∈[－t，t]的概率是( ).‎ A． B． C． D．‎ ‎7 ．右图是根据某赛季甲、乙两名篮球运动员每场比赛得分情况画出的茎叶图．‎ 从这个茎叶图可以看出甲、乙两名运动员得分的中位数分别是( ).‎ A．31，26 B．36，23 C．36，26 D．31，23‎ ‎8．按照程序框图(如右图)执行，第3个输出的数是( ).‎ A．3 B．4 C．5 D．6‎ ‎9．有一位同学家开了一个小卖部，他为了研究气温对热饮销售的影响，经过统计得到了一天所卖的热饮杯数(y)与当天气温(x℃)之间的线性关系，其回归方程为＝－2.35x＋147.77．如果某天气温为2℃时，则该小卖部大约能卖出热饮的杯数是( ).‎ A．140 B．143 C．152 D．156‎ ‎10．在下列各图中，两个变量具有线性相关关系的图是( ).‎ ‎(4)‎ ‎(3)‎ ‎(2)‎ ‎(1)‎ A．(1)(2) B．(1)(3) C．(2)(4) D．(2)(3) ‎ ‎11． 同时掷3枚硬币，至少有1枚正面向上的概率是 （　 　）.‎ Ａ． Ｂ． Ｃ． Ｄ．‎ ‎12．若以连续掷两次骰子分别得到的点数m，n作为点P的坐标，求点P落在圆x2＋y2＝16外部的概率是( ).‎ A． B． C． D．‎ 二、填空题：本大题共5个空，每空4分，共20分．‎ ‎13.图2是某学校一名篮球运动员在五场比赛中所得分数的茎叶图,则该运动员在这五场比赛中得分的方差为_______ ‎ ‎14.由经验得知，在某商场付款处排队等候付款的人数及其概率如下：‎ 排队人数 ‎0‎ ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5人以上 概 率 ‎0.1‎ ‎0.16‎ ‎0.3‎ ‎0.3‎ ‎0.1‎ ‎0.04‎ 则排队人数为2或3人的概率为 ．‎ ‎15．一个社会调查机构就某地居民的月收入调查了10 000人，并根据所得数据画了样本的频率分布直方图(如下图)．为了分析居民的收入与年龄、学历、职业等方面的关系，要从这10 000人中再用分层抽样方法抽出80人作进一步调查，则在[1 500，2 000)(元)月收入段应抽出 人．‎ ‎0.000 5‎ 频率 组距 ‎0.000 4‎ ‎0.000 3‎ ‎0.000 2‎ ‎0.000 1‎ 月收入/元 ‎1 000 1 500 2 000 2 500 3 000 3 500 4 000‎ 16. 口袋内装有100个大小相同的红球、白球和黑球,其中有45个红球,从中摸出1个球,摸出白球的概率为0.23,则摸出黑球的概率为____________.‎ ‎17、执行右图所示流程框图，若输入，则输出的值 为____________________．‎ 三、解答题：本大题共4小题，共32分 ‎18．(本小题满分7分) 从甲、乙两名学生中选拔一人参加射箭比赛，为此需要对他们的射箭水平进行测试．现这两名学生在相同条件下各射箭10次，命中的环数如下：‎ 甲 ‎8‎ ‎9‎ ‎7‎ ‎9‎ ‎7‎ ‎6‎ ‎10‎ ‎10‎ ‎8‎ ‎6‎ 乙 ‎10‎ ‎9‎ ‎8‎ ‎6‎ ‎8‎ ‎7‎ ‎9‎ ‎7‎ ‎8‎ ‎8‎ ‎(1)计算甲、乙两人射箭命中环数的平均数和标准差；(4分)‎ ‎(2)比较两个人的成绩，然后决定选择哪名学生参加射箭比赛．（3分）‎ 19． ‎(本小题满分7分) 某工厂为了对新研发的一种产品进行合理定价,将该产品按事先拟定的价格进行试销,得到如下数据:‎ ‎(I)求回归直线方程,其中（3分）‎ ‎(II)预计在今后的销售中,销量与单价仍然服从(I)中的关系,且 该产品的成本是4元/件,为使工厂获得最大利润,该产品的单价应定为多少元?(利润=销售收入—成本)（4分）‎ ‎20．(本小题满分8分) 在甲、乙两个盒子中分别装有标号为1，2，3，4的四个球，现从甲、乙两个盒子中各取出1个球，每个球被取出的可能性相等．‎ ‎(1)求取出的两个球上标号为相同数字的概率；（4分）‎ ‎(2)求取出的两个球上标号之积能被3整除的概率．（4分）‎ ‎21.(本小题满分10分)‎ 某校从参加高三模拟考试的学生中随机抽取60名学生，将其数学成绩(均为整数)分成六组[90,100)，[100,110)， [140,150)后得到如下部分频率分布直方图．观察图形的信息，回答下列问题．‎ ‎（Ⅰ）求分数在[120,130)内的频率；（2分） （Ⅱ）若在同一组数据中，将该组区间的中点值(如：组区间[100,110)的中点值为＝105)作为这组数据的平均分，据此估计本次考试的平均分；（2分） （Ⅲ）用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本，将该样本看成一个总体，从中任取2人，求至多有1人在分数段[120,130)内的概率．（6分）‎ 数学答案 一、选择题 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 ‎ B ‎ A ‎ A ‎ B ‎ A ‎ B C ‎ C ‎ ‎ B ‎ D A C 二、填空题 ‎13．6.8 14．0.6 15．16 16.0.32 17.- ‎ 三、解答题 ‎18、（7分） （1）解：(1)计算得＝8，＝8（2分）‎ ‎ s甲≈1.41，s乙≈1.10．（2分）‎ ‎(2)由(1)可知，甲、乙两名学生射箭命中环数的平均数相等，但s乙＜s甲，这表明乙的成绩比甲更稳定一些． 故选择乙参赛更合适．（3分）‎ ‎ ‎ 19、 ‎（7分）（1） ........（2分）‎ ‎ ..................（1分）‎ ‎ （2）工厂获得利润 ‎ .........（2分）‎ ‎ ‎ ‎ 当定价为元时，使工厂获得最大利润...（2分）‎ ‎20（8分）、解：设从甲、乙两个盒子中各取1个球，其数字分别为x，y.‎ 用(x，y)表示抽取结果，则所有可能的结果有16种，即 ‎(1，1)，(1，2)，(1，3)，(1，4)，(2，1)，(2，2)，(2，3)，(2，4)，‎ ‎(3，1)，(3，2)，(3，3)，(3，4)，(4，1)，(4，2)，(4，3)，(4，4)..........（2分）‎ ‎(1)设“取出的两个球上的标号相同”为事件A，‎ 则A＝{(1，1)，(2，2)，(3，3)，(4，4)}． ‎ 事件A由4个基本事件组成，故所求概率P(A)＝＝．.........（2分）‎ ‎ (2)设“取出的两个球上标号的数字之积能被3整除”为事件B，‎ 则B＝{(1，3)，(3，1)，(2，3)，(3，2)，(3，3)，(3，4)，(4，3)}.....(2分)‎ 事件B由7个基本事件组成，故所求概率P(A)＝.......（2分）‎ ‎21.（10分）（1）解：（Ⅰ）分数在[120,130)内的频率为； .......（2分）‎ ‎（2）估计平均分为 .....（2分）    （3）由题意，[110,120)分数段的人数为60×0.15＝9(人)．[120,130)分数段的人数为..1分                              ‎ ‎∵用分层抽样的方法在分数段为[110,130)的学生中抽取一个容量为6的样本， ∴需在[110,120)分数段内抽取2人，并分别记为在[120,130)分数段内抽取4人，并分别记为、、、；.....(1分)                  设“从样本中任取2人，至多有1人在分数段[120,130)内”为事件A，则基本事件共有，共15种．.....(1分)            则事件A包含的基本事件有，共9种．  ‎ ‎∴. .....(1分)   ‎ 从样本中任取2人，至多有1人在分数段[120,130)内的概率为.......(1分)‎