2018届二轮复习绝对值不等式课件（全国通用） 11页

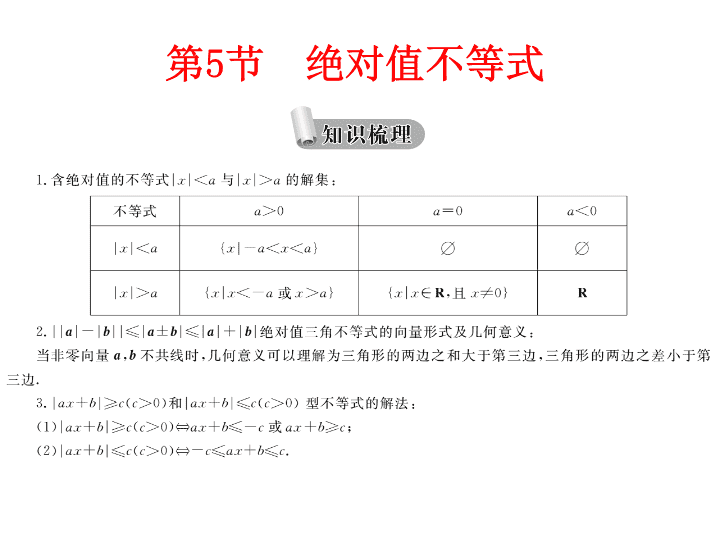
第二章　不等式 第 5 节 绝对值不等式 【 例 1】 解不等式 |x-1|≥2. 【 解析 】 由 | x- 1|≥2, 得到 x- 1≤ - 2 或 x- 1≥2, 所以 x ≤ - 1 或 x ≥3, 所以 | x- 1|≥2 的解集为 ( - ∞, - 1]∪[3,+∞) . 【 例 2】 解不等式 | x- 1|>| x | . 【解析】 将| x- 1|>| x |两边平方得到( x- 1) 2 > x 2 ,即 x 2 - 2 x +1> x 2 ,解得 x < , 所以| x- 1|>| x |的解集为{ x | x < } . 1 . (2010 陕西 )|2 x- 1|≤3 的解集为 . 【 答案 】 [ - 1,2] 【 解析 】 由 |2 x- 1|≤3 得到 - 3≤2 x- 1≤3, 解得 - 1≤ x ≤2, 所以 |2 x- 1|≤3 的解集为 [ - 1,2] . 2 . | x +1|≥1, 则 x 的取值范围是 . 【 答案 】 ( - ∞, - 2]∪[0,+∞) 【 解析 】 由 | x+ 1|≥1 得到 x +1≤ - 1 或 x +1≥1, 解得 x ≤ - 2 或 x ≥0 . 3 . | x- 1|+| x +3|≥6, 则 x 的取值范围是 . 5(2017 年山东卷 ) 设集合 M= { x || x- 1|<1}, N ={ x | x <2}, 则 M ∩ N= ( ) A.( - 1,1) B . ( - 1,2) C . (0,2) D . (1,2) 【 答案 】 C 【 解析 】 由 | x- 1|<1 得 0< x <2, 故 M ∩ N ={ x |0< x <2}∩{ x | x <2} = { x |0< x <2}, 选 C . 6 . (2013 大纲全国文科 ) 不等式 | x 2 - 2|<2 的解集是 ( ) A.( - 1,1) B.( - 2,2) C.( - 1,0)∪(0,1) D.( - 2,0)∪(0,2) 【 答案 】 D 【 解析 】 | x 2 - 2|<2⇒ - 2< x 2 - 2<2⇒0< x 2 <4⇒0<| x |<2⇒ - 2< x <0 或 0< x <2 . 故选 D . 7 . 设 a >0, 若不等式 | x-a |+|1 -x |≥1 对于任意 x ∈ R 恒成立 , 则 a 的最小值是 ( ) A.1 B. - 1 C.0 D.2 【 答案 】 D 【 解析 】 ∵| x-a |+|1 -x |≥| x-a +1 -x | = | a- 1|,∴| a- 1|≥1,∴ a ≤0 或 a ≥2 . ∵ a >0 . ∴ a ≥2 . 8 . (2011 广东高考 ) 不等式 | x +1|-| x- 3|≥0 的解集是 . 【 答案 】 { x | x ≥1} 【 解析 】 由 | x +1|-| x- 3|≥0 得 | x +1|≥| x- 3|, 两边平方得 x 2 +2 x +1≥ x 2 -6 x +9, 即 8 x ≥8, 解得 x ≥1, 所以原不等式的解集为 { x | x ≥1} . 9 . 对于实数 x , y , 若 | x- 1|≤1,| y- 2|≤1, 则 | x- 2 y +1| 的最大值为 . 【 答案 】 5 【 解析 】 | x- 2 y +1|=|( x- 1) - 2( y- 2) - 2|≤|( x- 1) - 2( y- 2)|+2 ≤| x- 1|+2| y- 2|+2=5 . 10 . (2013 江西高考 ) 在实数范围内 , 不等式 || x- 2|-1|≤1 的解集为 . 【 答案 】 [0,4] 【 解析 】 ∵|| x- 2|-1|≤1, ∴- 1≤| x- 2| - 1≤1,∴| x- 2|≤2, ∴ - 2≤ x- 2≤2,∴0≤ x ≤4 . 11 . (2012 天津高考 ) 集合 A= { x ∈R|| x- 2|≤5} 中的最小整数为 . 【 答案 】 - 3 【 解析 】 | x- 2|≤5⇒ - 3≤ x ≤7, 故 A 中最小整数是 - 3 . 12 .f ( x ) = |3 -x |+| x- 2| 的最小值为 . 【 答案 】 1 【 解析 】 ∵ |3 -x |+| x- 2|≥|(3 -x )+( x- 2)|=1,∴ f ( x ) min =1 . 13 . 不等式 | x +3|-| x- 2|≥3 的解集为 . 【 答案 】 { x | x ≥1} 【 解析 】 当 x ≥2 时 , 原不等式化为 x +3 - ( x- 2)≥3 . 解得 x ≥2; 当 - 3< x <2 时 , 原不等式化为 x +3 - (2 -x )≥3, 解得 1≤ x <2; 当 x ≤ - 3 时 , 原不等式化为 -x- 3 - (2 -x )≥3, 无解 . 综上 , x 的取值范围为 x ≥1 . 14 . 如果关于 x 的不等式 | x- 3|-| x- 4|< a 的解集不是空集 , 则实数 a 的取值范围是 . 【 答案 】 ( - 1,+∞) 【 解析 】 a >(| x- 3|-| x- 4|) min , 令 y= | x- 3|-| x- 4|, 由几何意义得 - 1≤ y ≤1, 故 a > - 1 . 15 . 已知函数 f ( x ) = | x- 4|-| x- 2| . (1) 作出函数 y=f ( x ) 的图象 ; (2) 解不等式 | x- 4|-| x- 2|>1 .