- 597.50 KB
- 2021-04-25 发布
试卷类型:A
肇庆市中小学教学质量评估
2019届高中毕业班第一次统一检测
理科数学
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分,共23小题,满分150分. 考试用时120分钟.
注意事项:
1. 答卷前,考生务必用黑色字迹的钢笔或签字笔,将自己所在县(市、区)、姓名、试
室号、座位号填写在答题卷上对应位置.
2. 选择题每小题选出答案后,用2B铅笔把答题卷上对应题目的答案标号涂黑;如需改
动,用橡皮擦干净后,再选涂其它答案,答案不能写在试卷或草稿纸上.
3. 非选择题必须用黑色字迹的钢笔或签字笔作答,答案必须写在答题卷各题目指定区域
内相应的位置上;如需改动,先划掉原来的答案,然后再在答题区内写上新的答案;
不准使用铅笔和涂改液.不按以上要求作答的答案无效.
第Ⅰ卷
一、 选择题:本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项是符合题目要求的.
(1)设集合,则
A. B. C. D.
(2)已知复数满足,则
A. B. C. D.
(3)设,,,则
A. B. C. D.
(4)设复数满足为虚数单位),则复数=
A. B. C. D.
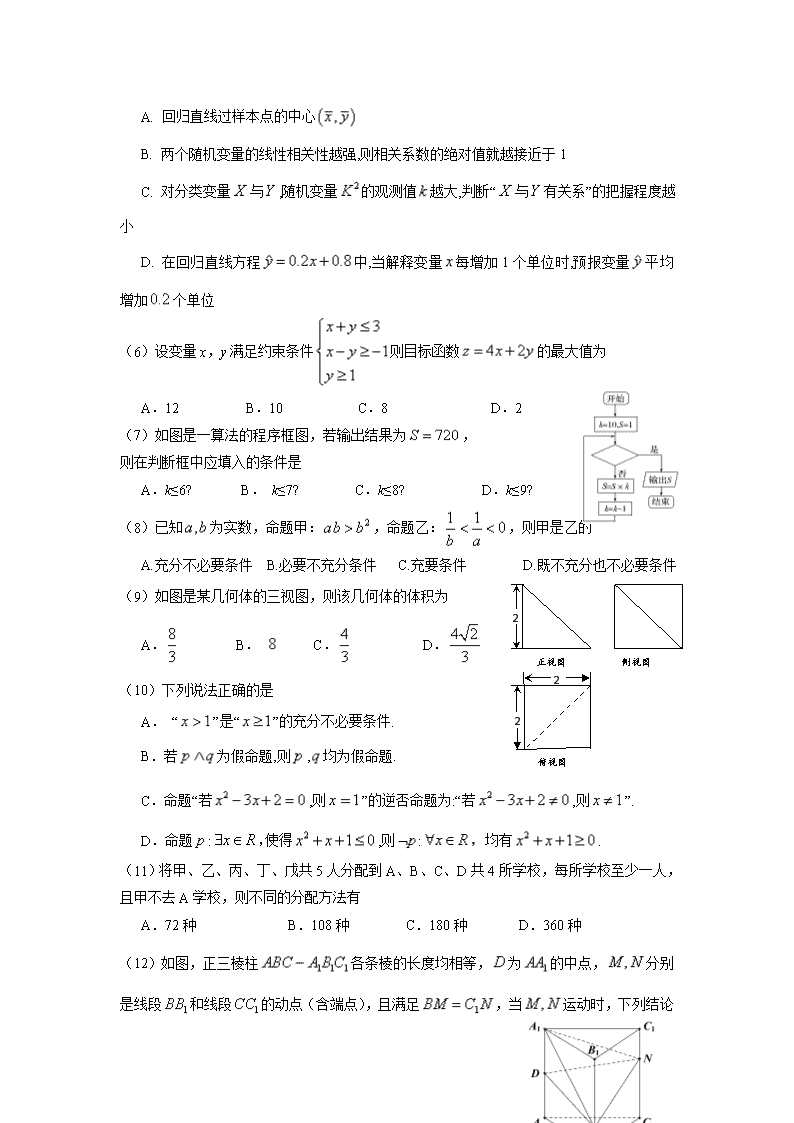
(5)下列说法错误的是
A. 回归直线过样本点的中心
B. 两个随机变量的线性相关性越强,则相关系数的绝对值就越接近于1
C. 对分类变量与,随机变量的观测值越大,判断“与有关系”的把握程度越小
D. 在回归直线方程中,当解释变量每增加1个单位时,预报变量平均增加个单位
(6)设变量x,y满足约束条件则目标函数的最大值为
A.12 B.10 C.8 D.2
(7)如图是一算法的程序框图,若输出结果为,
则在判断框中应填入的条件是
A.k≤6? B. k≤7? C.k≤8? D.k≤9?
(8)已知为实数,命题甲:,命题乙:,则甲是乙的
A.充分不必要条件 B.必要不充分条件 C.充要条件 D.既不充分也不必要条件
2
2
2
正视图
俯视图
侧视图
(9)如图是某几何体的三视图,则该几何体的体积为
A. B. C. D.
(10)下列说法正确的是
A. “”是“”的充分不必要条件.
B.若为假命题,则,均为假命题.
C.命题“若,则”的逆否命题为:“若,则”.
D.命题:使得,则: 均有.
(11)将甲、乙、丙、丁、戊共5人分配到A、B、C、D共4所学校,每所学校至少一人,且甲不去A学校,则不同的分配方法有
A.72种 B.108种 C.180种 D.360种
(12)如图,正三棱柱各条棱的长度均相等,为的中点,分别是线段和线段的动点(含端点),且满足,当
运动时,下列结论中不正确的是
A. 在内总存在与平面平行的线段
B. 平面平面
C. 三棱锥的体积为定值
D. 可能为直角三角形
第II卷
本卷包括必考题和选考题两部分. 第13题~第21题为必考题,每个试题考生都必须作答.第22题~第23题为选考题,考生根据要求作答.
二、填空题:本大题共4小题,每小题5分.
(13)若随机变量ξ~N(2,1),且,则= ▲ .
(14)的展开式中的系数是 ▲ .(用数字作答).
16题
(15)从一批次品率为0.02的产品中有放回地抽取100次,每次抽取一件产品,
设表示抽到的次品件数,则= ▲ .
(16)如图,在中,,,
若,则 ▲ .
三、解答题:解答应写出文字说明,证明过程或演算步骤.
(17)(本小题满分12分)
如图,在四棱锥,,底面是直角梯形,,,是的中点,是上一点,且.
(Ⅰ)证明:;
(Ⅱ)若,,求三棱锥
的体积.
(18)(本小题满分12分)
每年的金秋十月,越野e族阿拉善英雄会在内蒙古自治区阿拉善盟阿左旗腾格里沙漠举行,该项目已打造成集沙漠竞技运动、汽车文化极致体验、主题休闲度假为一体的超级汽车文化赛事娱乐综合体.为了减少对环境的污染,某环保部门租用了特制环保车清洁现场垃圾.通过查阅近5年英雄会参会人数(万人)与沙漠中所需环保车辆数量(辆),得到如下统计表:
参会人数(万人)
11
9
8
10
12
所需环保车辆(辆)
28
23
20
25
29
(Ⅰ)根据统计表所给5组数据,求出关于的线性回归方程.
(Ⅱ)已知租用的环保车平均每辆的费用(元)与数量(辆)的关系为
.主办方根据实际参会人数为所需要投入使用的环保车,
每辆支付费用6000元,超出实际需要的车辆,主办方不支付任何费用.预计本次英雄会大约有14万人参加,根据(Ⅰ)中求出的线性回归方程,预测环保部门在确保清洁任务完成的前提下,应租用多少辆环保车?获得的利润是多少?(注:利润主办方支付费用租用车辆的费用).
参考公式:
(19)(本小题满分12分)
如图,在四棱锥中,面面,底面
是边长为2的正方形,且,.
(Ⅰ)证明:;
(Ⅱ)求面与面所成二面角的正弦值.
(20)(本小题满分12分)
某工厂生产的某产品按照每箱10件包装,每箱产品在流入市场之前都要检验.若整箱产品检验不通过,除去检验费用外,每箱还要损失100元.检验方案如下:
第一步,一次性随机抽取2件,若都合格则整箱产品检验通过;若都不合格则整箱产品检验不通过,检验结束,剩下的产品不再检验.若抽取的2件产品有且仅有1件合格,则进行第二步工作.
第二步,从剩下的8件产品中再随机抽取1件,若不合格,则整箱产品检验不通过,检验结束,剩下的产品不再检验.若合格,则进行第三步工作.
第三步,从剩下的7件产品中随机抽取1件,若不合格,则整箱产品检验不通过,若合格,则整箱产品检验通过,检验结束,剩下的产品都不再检验.
假设某箱该产品中有8件合格品,2件次品.
(Ⅰ)求该箱产品被检验通过的概率;
(Ⅱ)若每件产品的检验费用为10元,设该箱产品的检验费用和检验不通过的损失费用之和为,求的分布列和数学期望.
(21)(本小题满分12分)
如图,在四棱锥中,底面是边长为的正方形,,是的中点,是线段上异于端点的一点,平面平面,.
(Ⅰ)证明:;
(Ⅱ)若与面所成的角的正弦值为,
求四棱锥的体积.
请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分. 作答时,
请用2B铅笔在答题卡上将所选题号后的方框涂黑.
(22)(本小题满分10分)选修4-4:坐标系与参数方程
在直角坐标系中,直线的参数方程为(为参数),以坐标原点为极点,
轴正半轴为极轴建立极坐标系,曲线的极坐标方程为.
(Ⅰ)求和的直角坐标方程;
(Ⅱ)若曲线截直线所得线段的中点坐标为,求的斜率.
(23)(本小题满分10分)选修4—5:不等式选讲
设函数.
(Ⅰ)当时,求不等式的解集;
(Ⅱ)若恒成立,求的取值范围.