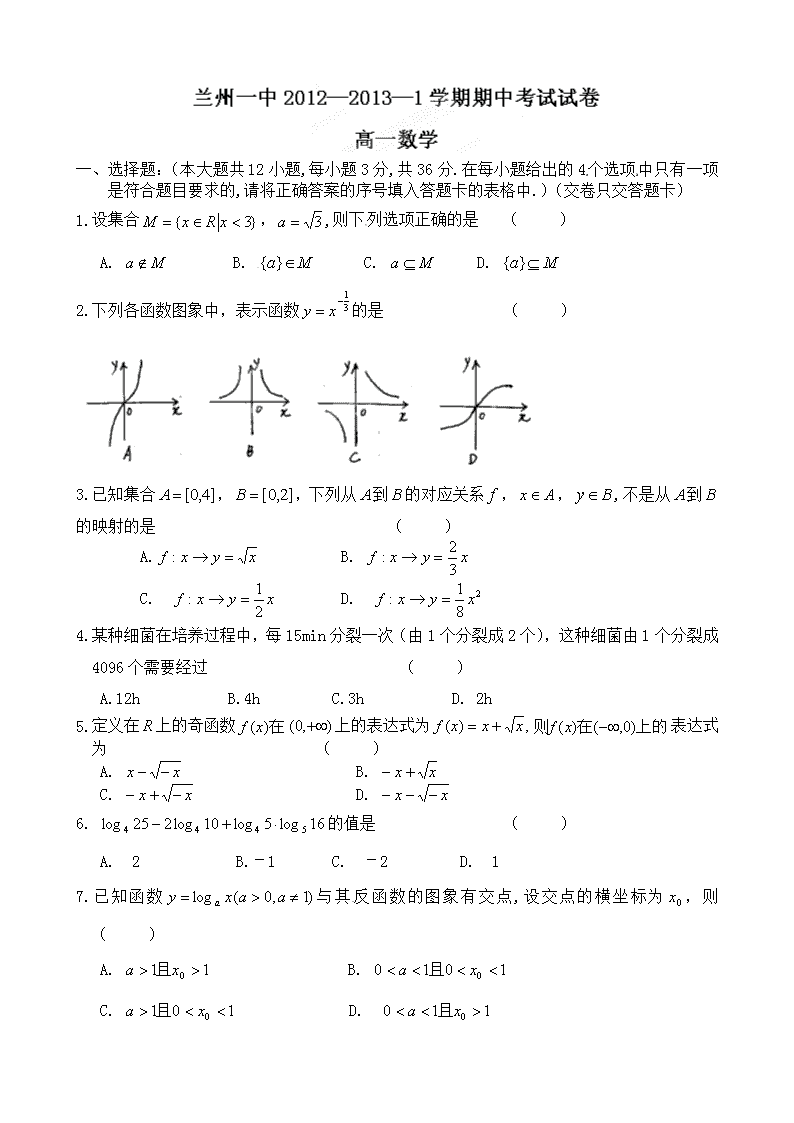甘肃省兰州一中2012-2013学年高一上学期期中考试数学试题 5页

‎ ‎ 一、选择题：（本大题共12小题,每小题3分,共36分.在每小题给出的4个选项中只有一项是符合题目要求的,请将正确答案的序号填入答题卡的表格中.）（交卷只交答题卡）‎ ‎1.设集合，,则下列选项正确的是 （ ）‎ A. B. C. D. ‎ ‎2.下列各函数图象中，表示函数的是 （ ）‎ ‎3.已知集合，，下列从到的对应关系，，,不是从到的映射的是 （ ）‎ A. B. ‎ ‎ C. D. ‎ ‎4.某种细菌在培养过程中，每15min分裂一次（由1个分裂成2个），这种细菌由1个分裂成4096个需要经过 （ ）‎ A.12h B.4h C.3h D. 2h ‎5.定义在上的奇函数上的表达式为 表达式为 （ ） ‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎6. 的值是 （ ）‎ A. 2 　 B.－‎1 ‎　　 C. －2　　　 D.　1‎ ‎7.已知函数与其反函数的图象有交点,设交点的横坐标为，则 （ ）‎ A. B. ‎ C. D. ‎ ‎8.已知则的大小关系是 （ ）‎ A. B. C. D. ‎ ‎9.设是定义在上的偶函数，它在上为增函数，且，则不等式的解集为 （ ）‎ ‎ A. B. ‎ ‎ C. D. ‎ ‎10.设函数则函数 （ ）‎ A.在区间内均有零点 ‎ ‎ B.在区间内均无零点 C.在区间内有零点，在区间内无零点 D.在区间内无零点，在区间内有零点 ‎11.已知在上为减函数，则的取值范围为（ ）‎ A.（0，1） B. （0，2） C. （1，2） D. ‎ ‎12.设奇函数在上是增函数，且，若对所有的及任意的都满足，则的取值范围是（ ）‎ ‎ A. B. ‎ C. D. ‎ 二、填空题 ：(本大题共4小题，每小题4分，共16分)‎ ‎13.函数的定义域是 . ‎ ‎14.函数的单调递减区间是 .‎ ‎15.若函数，则的值为 .‎ ‎16.函数对有意义，且满足，,为增函数．如果，则实数的取值范围是 . ‎ 三、解答题：（写出必要的计算步骤、解答过程，只写最后结果的不得分，共48分.）‎ ‎17.(本小题8分)（1）(4分)求值 ‎（2）(4分) 设，求函数的最大值和最小值. ‎18. (本小题8分)求实数的取值范围，使关于的方程 ‎ ‎（1）有两个实根，且都大于1.‎ ‎（2）有两个实根、，且满足.‎ ‎19.(本小题10分)设 ‎ （1）若，求 的值.‎ ‎ （2）若，求 的值.‎ ‎20. (本小题10分)已知函数. ‎(1)若的定义域为，求实数的范围. ‎(2)若的值域为，求实数的范围.‎ ‎21. (本小题12分)已知函数. ‎ ‎(1) 当时，求的定义域、值域. ‎ ‎(2) 当时，判断的单调性,并用定义证明.‎ ‎（3）解不等式.‎ 兰州一中2012—2013—1学期高一年级数学期中试卷答案 一、选择题：（本大题共12小题,每小题3分,共36分）‎ 题号 ‎1‎ ‎2‎ ‎3‎ ‎4‎ ‎5‎ ‎6‎ ‎7‎ ‎8‎ ‎9‎ ‎10‎ ‎11‎ ‎12‎ 答案 D C B C A D B C A D C A 二、填空题 ：(本大题共4小题，每小题4分，共16分)‎ ‎13. 14. 15. 16. ‎ 三、解答题：（共48分）17. (本小题8分)（1）解:19‎ ‎18. (本小题8分)（1） ‎ ‎（2） ‎ ‎（2）由，又，故 ‎①当时，， 解得；‎ ‎②当时， ，解得，‎ 此时，满足；‎ ‎③当时，， 解得.‎ 综上所述，实数的取值范围是或者.‎ ‎20. (本小题10分)解：(1)若f(x)的定义域为R，则关于x的不等式ax2＋2x＋1＞0的解集为R，即，解得a＞1 ‎(2)若f(x)的值域为R，则ax2＋2x＋1能取一切正数 ‎∴a＝0或，解得0≤a≤1 ‎=0,即f(x1)＞f(x2).∴f(x)为减函数.‎ ‎(3) 当时，x2－2＜x,即 x2－x－2＜0,解得－1＜x＜2.‎ 又函数f(x)定义域为(－∞,1),即故所求不等式的解为－1＜x＜1.‎ 当时， ＞,∴＞ax,∴x2－2＜x，解得－1＜x＜2. 又函数f(x)的定义域为(1，+∞)，即 故所求不等式的解为 综上，当时，所求不等式的解集为 当时，所求不等式的解集为 ‎ ‎