- 421.50 KB
- 2021-04-23 发布
2017-2018学年广西省贵港市覃塘高级中学高二12月月考
理科数学
试卷说明:本试卷分Ⅰ卷和Ⅱ卷,Ⅰ卷为试题(选择题和客观题),学生自已保存,Ⅱ卷一般为答题卷,考试结束只交Ⅱ卷。
一、选择题(本大题共12小题,每小题5分,在每小题给出的四个选项中,只有一项符合题目的要求)
1.命题“若,则”的逆否命题是( )
A.若,则 B.若,则
C.若,则 D.若,则
2《九章算术》勾股章有一“引葭赴岸”问题;“今有池方一丈,葭生其中央,出水两尺,引葭赴岸,适与岸齐。问水深、葭长各几何?”其意思是:有一水池一丈见方。池中心有一颗类似芦苇的植物,露出水面两尺,若把它引向岸边,正好与岸边齐,问水有多深,该植物有多长?其中一丈为十尺,若从该葭上随机一点,则该点取水下的概率是( )
3.一次猜奖游戏中,1,2,3,4四扇门里摆放了a,b,c,d四件奖品(每扇门里仅放一件),甲同学说:1号门里是b,3号门里是c;乙同学说:2号门里是b,3号门里是d;丙同学说:4号门里是b,2号门里是c;丁同学说:4号门里是a,3号门里是c。如果他们每人都猜对一半,那么4号门里是( )
A a B b C c D d
4.2013年各月的平均气温()数据的茎叶图如下: 则这组数据的中位数是( )
A、19 B、20 C、21.5 D、23
5.过点(2,-1)引直线与抛物线只有一个公共点,这样的直线共有( )条
A. 1 B.2 C. 3 D.4
6.阅读如图13所示的程序框图,运行相应的程序,则程序运行后输出的结果为( )
图13
A.7 B.9 C.10 D.11
7.“0≤a<2”是“ax2+2ax+1>0的解集是实数集R”的( )
A.充分而非必要条件 B.必要而非充分条件 C.充要条件 D.既非充分也非必要条件
8.如果椭圆的弦被点(4,2)平分,则这条弦所在的直线方程是( )
A B C D
9. 已知正四棱柱ABCD-A1B1C1D1中,AB=2,CC1=2,E为CC1的中点,则直线AC1与平面BED的距离为 ( )A.2 B. C. D.1
11..直线y=x-1与抛物线相交于 M.N两点,抛物线的焦点为F,设,的值为 ( )
12.已知F1,F2分别是双曲线﹣=1(a>0,b>0)的左、右焦点,点P在双曲线上且不与顶点重合,过F2作∠F1PF2的角平分线的垂线,垂足为A.若|OA|=b,则该双曲线的离心率为( )
A. B. C. D.
二、 填空题
13.设双曲线的右焦点为F2,则F2到渐近线的距离为______
14.在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中点,E,F分别是CC1,AD的中点,那么异面直线OE和FD1所成的角的余弦值等于________.
15.以下命题
①“”是“”的充分不必要条件
②命题“若”的逆否命题为“若”
③对于命题,则
④若为假命题,则p、q均为假命题
其中正确命题的序号为 ▲ (把所有正确命题的序号都填上
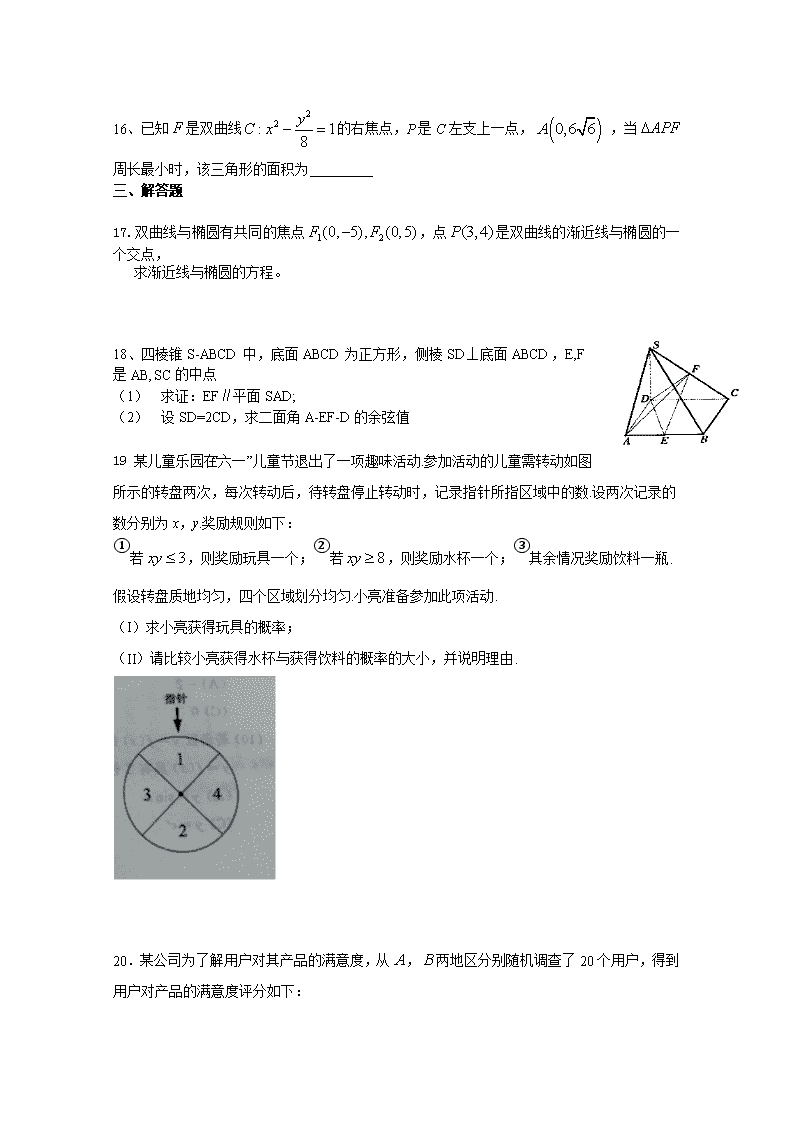
16、已知是双曲线的右焦点,P是C左支上一点, ,当周长最小时,该三角形的面积为
三、解答题
17.双曲线与椭圆有共同的焦点,点是双曲线的渐近线与椭圆的一个交点,
求渐近线与椭圆的方程。
18、四棱锥S-ABCD中,底面ABCD为正方形,侧棱SD⊥底面ABCD,E,F是AB,SC的中点
(1) 求证:EF∥平面SAD;
(2) 设SD=2CD,求二面角A-EF-D的余弦值
19 某儿童乐园在“六一”儿童节退出了一项趣味活动.参加活动的儿童需转动如图所示的转盘两次,每次转动后,待转盘停止转动时,记录指针所指区域中的数.设两次记录的数分别为x,y.奖励规则如下:
①若,则奖励玩具一个;②若,则奖励水杯一个;③其余情况奖励饮料一瓶.
假设转盘质地均匀,四个区域划分均匀.小亮准备参加此项活动.
(I)求小亮获得玩具的概率;
(II)请比较小亮获得水杯与获得饮料的概率的大小,并说明理由.
20.某公司为了解用户对其产品的满意度,从,两地区分别随机调查了20个用户,得到用户对产品的满意度评分如下:
A地区:62 73 81 92 95 85 74 64 53 76 78 86 95 66 97 78 88 82 76 89
B地区:73 83 62 51 91 46 53 73 64 82 93 48 65 81 74 56 54 76 65 79
(Ⅰ)根据两组数据完成两地区用户满意度评分的茎叶图,并通过茎叶图比较两地区满意度评分的平均值及分散程度(不要求计算出具体值,得出结论即可);
(Ⅱ)根据用户满意度评分,将用户的满意度从低到高分为三个等级:
满意度评分
低于70分
70分到89分
不低于90分
满意度等级
不满意
满意
非常满意
记事件C:“A地区用户的满意度等级高于B地区用户的满意度等级”.假设两地区用户的评价结果相互独立.根据所给数据,以事件发生的频率作为相应事件发生的概率,求C的概率.
21如图,在四棱锥中,平面平面,
,,,,,.
(I)求证:平面;
(II)求直线PB与平面PCD所成角的正弦值;
(III)在棱PA上是否存在点M,使得BM∥平面PCD?若存在,求的值;若不存在,说明理由.
22、 椭圆的右焦点为F1(2,0),过F1作圆的切线交Y轴于点Q,切点N为F1Q的中点。
(1)求椭圆的方程,(2)曲线与椭圆交于A,B.C.D四点,若这四个点都在同一圆上,求这圆的圆心坐标.