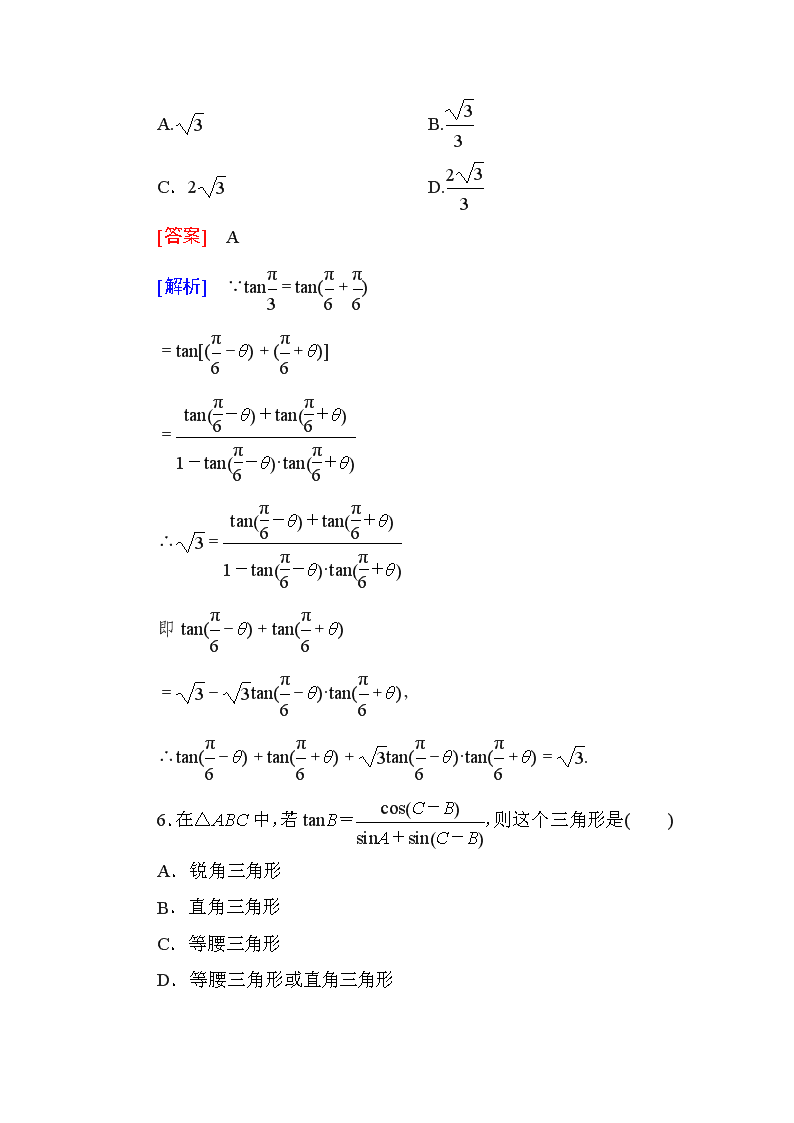- 79.50 KB
- 2021-04-23 发布
能 力 提 升
一、选择题
1.tan(α+β)=,tan(α-β)=,则tan2α=( )
A. B.
C. D.
[答案] D
[解析] tan2α=tan[(α+β)+(α-β)]
===.
2.(2013长春二模)在△ABC中,若tanAtanB=tanA+tanB+1,则cosC的值是( )
A.- B.
C. D.-
[答案] B
[解析] 由tanA·tanB=tanA+tanB+1,可得=-1,即tan(A+B)=-1,∵A+B∈(0,π),∴A+B=,则C=,cosC=.
3.在△ABC中,若00,
∴cosA<0,∴A为钝角.
4.已知tanα、tanβ是方程x2+3x+4=0的两根,且-<α<,-<β<,则α+β的值为( )
A. B.-
C.或- D.-或
[答案] B
[解析] 由韦达定理得
tanα+tanβ=-3,tanα·tanβ=4,
∴tanα<0,tanβ<0,
∴tan(α+β)===
又-<α<,-<β<,且tanα<0,tanβ<0
∴-π<α+β<0,∴α+β=-.
5.(2011~2012·长春高一检测)tan(-θ)+tan(+θ)+tan(-θ)tan(+θ)的值是( )
A. B.
C.2 D.
[答案] A
[解析] ∵tan=tan(+)
=tan[(-θ)+(+θ)]
=
∴=
即tan(-θ)+tan(+θ)
=-tan(-θ)·tan(+θ),
∴tan(-θ)+tan(+θ)+tan(-θ)·tan(+θ)=.
6.在△ABC中,若tanB=,则这个三角形是( )
A.锐角三角形
B.直角三角形
C.等腰三角形
D.等腰三角形或直角三角形
[答案] B
[解析] 因为△ABC中,A+B+C=π,
所以tanB=
==,
即=,
∴cos(B+C)=0,∴cos(π-A)=0,∴cosA=0,
∵0