2018届二轮复习客观题专题七函数与导数课件（25张)（全国通用） 25页

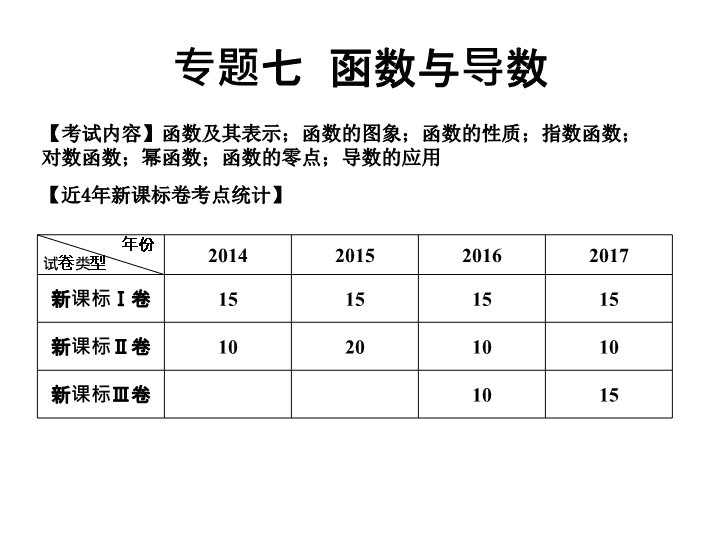
专题七 函数与导数 【近 4 年新课标卷考点统计 】 【 考试内容 】 函数及其表示；函数的图象；函数的性质；指数函数； 对数函数；幂函数；函数的零点；导数的应用 年份 试卷类型 2014 2015 2016 2017 新课标Ⅰ卷 15 15 15 15 新课标Ⅱ卷 10 20 10 10 新课标 Ⅲ 卷 10 15 一、函数的基本性质 1 . 函数的单调性: (1) f ( x )在区间 M 上是增函数⇔∀ x 1 , x 2 ∈ M ,当 x 1 < x 2 时,有 f ( x 1 )< f ( x 2 ); (2) f ( x )在区间 M 上是减函数⇔∀ x 1 , x 2 ∈ M ,当 x 1 < x 2 时,有 f ( x 1 )> f ( x 2 ) . (记忆方法:不等号相同为增,不同为减,即同增异减) 2 . 函数的奇偶性: (1)奇函数、偶函数的定义: 如果对于函数 f ( x )的定义域内的任意一个 x ,都有 f ( -x )= f ( x ) ,则称函数 y = f ( x )是偶函数; 如果对于函数 f ( x )的定义域内的任意一个 x ,都有 f (- x )=- f ( x ) ,则称函数 y = f ( x )是奇函数 . (2)奇、偶函数的性质: ①偶函数的图象关于 y 轴 对称;奇函数的图象关于 原点 对称 . ②奇函数 f ( x )的定义域中若含有0,则必有 f (0)= 0 . (3)常见的奇函数与偶函数: ①常见的奇函数: 正比例函数: f ( x )= kx ( x ∈R); 反比例函数: f ( x )= ( x ∈(-∞,0)∪(0,+∞)); 正弦函数: f ( x )=sin x ( x ∈R); 正切函数: f ( x )=tan x ; 幂函数: f ( x ) = x n ( x ∈R)当 n 为奇数时 f ( x )= x n 为奇函数 . 几种特殊的奇函数: f ( x )=| x +1|-| x -1| ②常见的偶函数: 余弦函数: f ( x )=cos x ( x ∈R); 幂函数: f ( x )= x n ( x ∈R)当 n 为偶数时 f ( x )= x n 为偶函数 . 几种特殊的偶函数: f ( x ) =c ( c 为常数); f ( x )=| x |; f ( x )= ; f ( x )=| x +1|+| x -1|. ③在定义域符合要求的前提下: 奇函数与奇函数的和是奇函数;偶函数与偶函数的和是偶函数; 奇函数与奇函数的积是偶函数;偶函数与偶函数的积是偶函数; 奇函数与偶函数的积是奇函数;奇函数与偶函数的和是非奇非偶函数; 如: f ( x )= ax 3 + bx , f ( x )= ax + 是奇函数; f ( x )= ax 2 + c , f ( x )= ax 4 + bx 2 + c , f ( x )= · x 是偶函数; f ( x )= x 2 - x +1是非奇非偶函数 . (6)指数函数: y = a x ( a >0, a ≠1) 图象恒过点(0,1),单调性与 a 的值有关,在解题中,往往要对 a 分 a >1和0< a <1两种情况进行讨论,要能够画出函数图象的简图 . (7)对数函数: y =log a x ( a >0, a ≠1) 图象恒过点(1,0),单调性与 a 的值有关,在解题中,往往要对 a 分 a >1和0< a <1两种情况进行讨论,要能够画出函数图象的简图 . (8)注意的几个问题: ① y = a x 与 y =log a x 的图象关系是关于直线 y=x 对称;这两个函数互为反函数 . ②比较两个指数式或对数式的大小的基本方法是构造相应的指数或对数函数,若底数不相同时转化为同底数的指数或对数,还要注意与1或0比较. 4 . 导数的应用: (1)求切线的斜率,以及求切线方程 . (2)利用导数判断函数的单调性: 若 f' ( x )>0, x ∈( a , b ) 则 f ( x ) 在 ( a,b ) 上为增函数; 若 f' ( x )<0 , x∈ ( a,b) 则 f ( x ) 在 ( a,b ) 上为减函数 . (3)单调区间的求解过程,已知 y = f ( x ) ①分析 y = f ( x ) 的定义域; ②求导数 y' = f' ( x ) ; ③解不等式 f' ( x )>0 ,解集在定义域内的部分为增区间; ④解不等式 f' ( x )<0 ,解集在定义域内的部分为减区间. 考点训练 A 考点训练 考点训练 D A 考点训练 9 . 下列函数为偶函数的是 ( ) A. y= sin x B. y=x 3 C. y=e x D. y= ln 考点训练 D 10 . 若函数 f ( x )=3 x +3 - x 与 g ( x )=3 x -3 - x 的定义域均为R,则 ( ) A .f ( x )与 g ( x )均为偶函数 B .f ( x )为奇函数, g ( x )为偶函数 C .f ( x )与 g ( x )均为奇函数 D .f ( x )为偶函数, g ( x )为奇函数 考点训练 D 16 . 若 a > b >0,0< c <1,则 ( ) A . log a c c b 考点训练 B 20 . 若 a >0, b >0,且函数 f ( x )=4 x 3 - ax 2 -2 bx +2在 x =1处有极值,则 ab 的最大值等于 ( ) A.2 B.3 C.6 D.9 考点训练 D 21 . 函数 f ( x )= e x + x -2的零点所在的一个区间是 ( ) A.(-2,-1) B.(-1,0) C.(0,1) D.(1,2) 考点训练 C 考点训练 详见 《 艺考生文化课冲刺点金 · 数学 》 书中 P32-33 其他题