- 2.99 MB
- 2021-04-23 发布
高三教学质量检测考试
文科数学 2018.2[来
本试卷分为选择题和非选择题两部分,共4页.满分150分.考试用时120分钟.
注意事项:
1.答题前,考生务必用直径0.5毫米黑色墨水签字笔将自己的姓名、考生号和座位号填写在答题卡上和试卷规定的位置上.
2.第Ⅰ卷每小题选出答案后,用2B铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案序号,答案不能答在试卷上.
3.第Ⅱ卷必须用0.5毫米黑色签字笔作答,答案必须写在答题卡各题目指定区域内相应的位置,不能写在试卷上;如需改动,先划掉原来的解答,然后再写上新的解答;不准使用涂改液、胶带纸、修正带.不按以上要求作答的答案无效.
第Ⅰ卷(共60分)
一、选择题:本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.已知集合,,则( )
A. B. C. D.
2.若复数,则实数( )
A. B. C. D.
3. 一只昆虫在半径为3的圆形区域内自山爬行,则其到边界的距离大于1的概率为( )
A. B. C. D.
4. 过双曲线的右焦点且与轴垂直的直线,交该双曲线的两条渐近线于A,B两点,则
A. B. C. D.
5. 在中,,,对角线AC,BD交于点O,则的坐标为
A. B. C. D.
6. 中国古代数学著作《算法统宗》中有这样一个问题:“三百七十八里关,初步健步不为难,次日脚疼减一半,六朝才得到其关,要见次日行里数,请公仔仔细算相还.”其大意为:“有一个人走378里路,第一天健步行走,从第二天起脚疼每天走的路程为前一天的一半,走了6天后到达目的地”则该人第4天走的路程为
A.6里 B.12里 C.24里 D.48里
7. 已知不等式组表示的平面区域被圆C及其内部所覆盖,当圆C的面积最小时,圆C的方程是
A. B.
C. D.
8. 如图,格纸上正方形的边长为1,图中粗实线画出的是一个几何体的三视图,
则这个几何体的体积是
A. B. C. D.
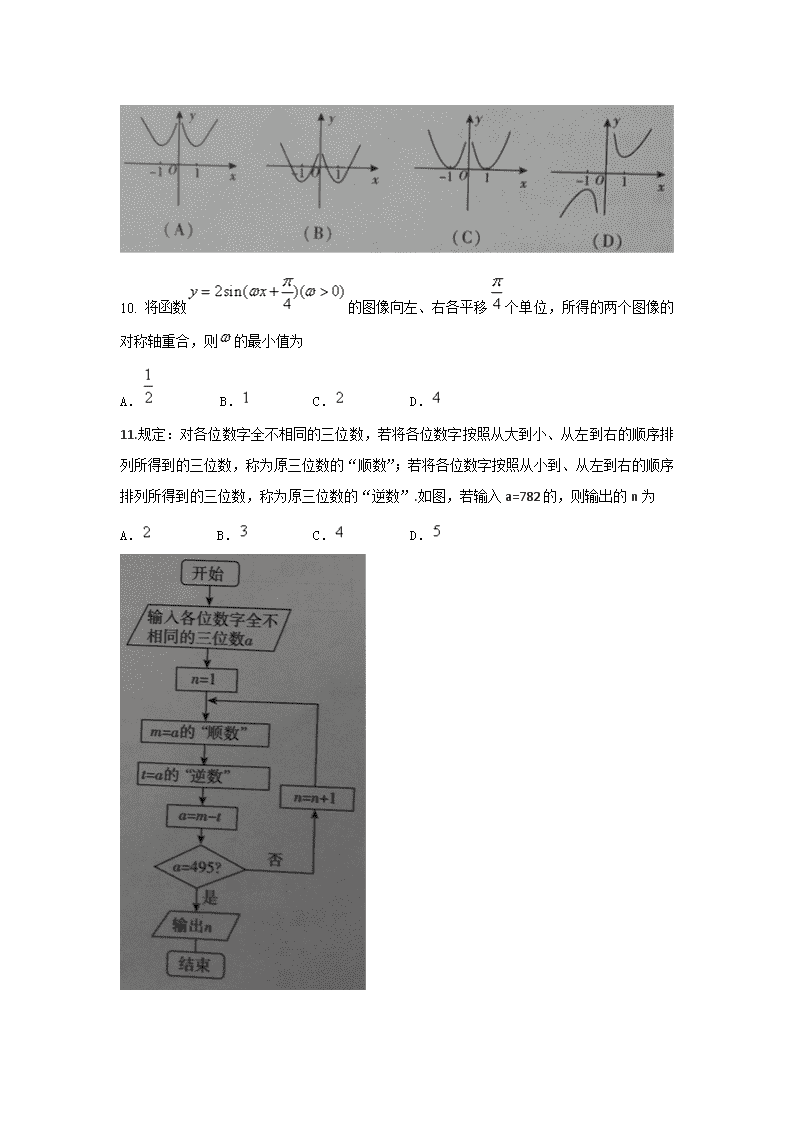
9. 已知函数,则函数的大致图像是
10. 将函数的图像向左、右各平移个单位,所得的两个图像的对称轴重合,则的最小值为
A. B. C. D.
11.规定:对各位数字全不相同的三位数,若将各位数字按照从大到小、从左到右的顺序排列所得到的三位数,称为原三位数的“顺数”;若将各位数字按照从小到、从左到右的顺序排列所得到的三位数,称为原三位数的“逆数”.如图,若输入a=782的,则输出的n为
A. B. C. D.
12.过抛物线C:的焦点F的直线l交抛物线C于A,B两点,若抛物线C在点B处的切线斜率为2,则线段
A. B. C. D.
第Ⅱ卷(共90分)
二、填空题:本大题共4小题,每小题5分,共20分.
13.已知是等差数列,若则
14.已知,则
15.已知奇数在R上是增函数,函数.若,则把a,b,c按从小到大的顺序用不等号连接起来为
16.已知A,B,C,D是同一球面上的四个点,其中△ABC是正三角形,AD⊥平面ABC,AD=2AB=6,则该球的表面积为
三、解答题:共70分.解答时应写出必要的文字说明、证明过程或运算步骤.
17. (本小题满分12分)
在△ABC中,a,b,c分别为角A,B,C的对边长,已知.
(1)求角B;
(2)若b=6,△ABC的面积,求a
18. (本小题满分12分)
某城市先后采用甲、乙两种方案治理空气污染各一年,各自随机抽取一年(365天)内100
天的空气质量指数API的检测数据进行分析,若空气质量指数值在[0,300]内为合格,否则为不合格.表1是甲方案检测数据样本的频数分布表,图l是乙方案检测数据样本的频率分布直方图.
API值
[0,50]
(50,100]
(100,150]
(150,200]
(200,250]
(250,300]
大于300
天数
9
13
19
30
14
11
4
(1)将频率视为概率,求乙方案样本的频率分布直方图中a的值,以及乙方案样本的空
气质量不合格天数;
(2)根据图1,求乙方案样木的中位数;
(3)填写下面2×2列联表,并根据列联表判断是否有90%的把握认为该城市的空气质
量指数值与两种方案的选择有关.
甲方案
乙方案
合计
合格天数
不合格天数
合计
附:
P(K2≥k)
0.10
0.05
0.025
k
2.706
3.841
5.024
19. (本小题满分12分)
如图,三棱柱的侧面为正方形,,D是AB的中点,
(1)求证:平面;
(2)若,求三棱柱的体积。
20. (本小题满分12分)
已知椭圆,抛物线的焦点均在x轴上,的中心和的顶点均为原点O,从每条曲线上各取两个点,将其坐标记录在下表中
x
-3
-2
-4
y
0
-4
(1)求,的标准方程;
(2)是否存在直线l满足条件:①直线l过曲线的焦点;②直线l与曲线交于不同
的两点A,B,且△AOB的面积是.若存在,求出直线l的万程;若不存在,请说明理由.
21. (本小题满分12分)
已知函数.
(1)讨论的单调性;
(2)若,证明:函数在区间上有极大值,且极大值小于0.
请考生在第22~23两题中任选一题作答,如果多做,则按所做的第一题计分.做答时请写清题号.
22. (本小题满分10分) 选修4-4:坐标系与参数方程.
在平面直角坐标系中,直线过点,倾斜角为,P为上的动点,设.以坐标原点为极点,以轴的正半轴为极轴建立极坐标系,曲线C的极坐标方程为,直线与曲线C的交点为A,B.
(1)求直线以t为参数的方程和曲线C的普通方程;
(2)求的值.
23. (本小题满分10分) 选修4-5:不等式选讲.
设函数,其中.
(1)当时,求不等式的解集;
(2)若不等式的解集为,求实数的值.
曲线C的极坐标方程为,两边同乘可得曲线C的一般方程为:;(2)将直线以t为参数的方程(t为参数)代入曲线得:
,,因为在直线上,所以
.
23. 设函数,其中.
(1)当时,求不等式的解集;
(2)若不等式的解集为,求实数的值.
解:(1)当时,,
,即,
当时,原不等式可化为,解得,
当时,原不等式可化为,解得不等式无解,
当时,原不等式可化为,解得,
综上,原不等式的解集为
(2)由题意得,不等式可化为,
即,可得,解得,由不等式的解集为,得,解得.