- 458.00 KB
- 2021-04-23 发布
全*品*高*考*网, 用后离不了!
一、填空题:本大题共14小题,每小题5分,共70分.把答案填写在答题卡相应的位置上.
1.命题“x∈R,x2+x+1≤0”的否定是 .
【答案】∀x∈R,x2+x+1>0
【解析】
试题分析:特称命题的否定是全称命题,并将结论加以否定:所以命题“x∈R,x2+x+1≤0”的否定是:∀x∈R,x2+x+1>0
考点:全称命题与特称命题
2.若点P(a,3)在不等式2x+y<3表示的区域内,则实数a的取值范围是
【答案】a<0
【解析】
试题分析:由题意可知将P(a,3)代入不等式2x+y<3成立,所以
考点:不等式表示平面区域
3.函数y=lg(x2﹣3x+2)的定义域为
【答案】(﹣∞,1)∪(2,+∞)
【解析】
试题分析:要使函数有意义,需满足或,定义域为(﹣∞,1)∪(2,+∞)
考点:函数定义域
4.若椭圆,则实数的取值范围是 .
【答案】
【解析】
试题分析:由方程可知
考点:椭圆性质
5.已知p:0<m<1,q:椭圆+y2=1的焦点在y轴上,则p是q的 条件.(填“充
分不必要”、“必要不充分”、“充要”或“既不充分也不必要”填空)
【答案】充要
【解析】
试题分析:椭圆 +y2=1的焦点在y轴上,所以,所以p是q的充要条件
考点:充分条件与必要条件
6.已知x<0,则的最大值等于________.
【答案】
【解析】
试题分析:,当且仅当时等号成立,取得最小值
考点:均值不等式求最值
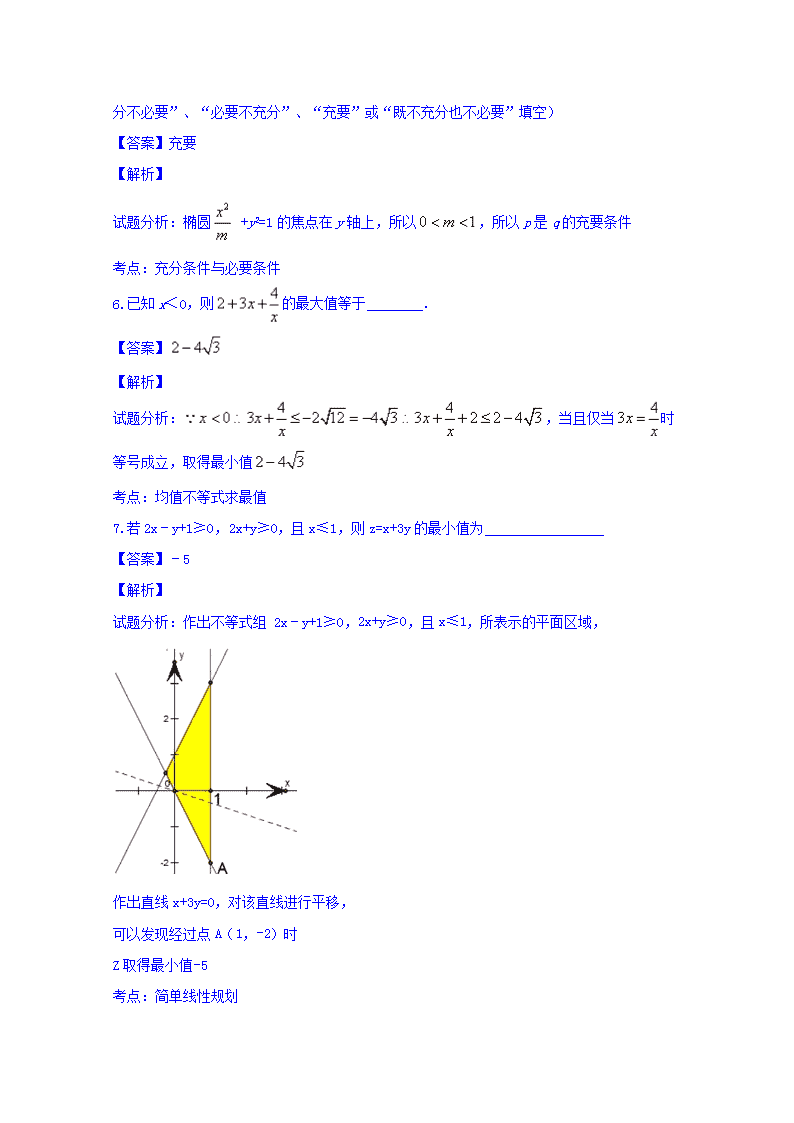
7.若2x﹣y+1≥0,2x+y≥0,且x≤1,则z=x+3y的最小值为
【答案】﹣5
【解析】
试题分析:作出不等式组 2x﹣y+1≥0,2x+y≥0,且x≤1,所表示的平面区域,
作出直线x+3y=0,对该直线进行平移,
可以发现经过点A(1,-2)时
Z取得最小值-5
考点:简单线性规划
8.已知方程表示椭圆,则k的取值范围为___________________
【答案】(3,4)∪(4,5)
【解析】
试题分析:,解不等式得取值范围(3,4)∪(4,5)
考点:椭圆方程与性质
9.已知命题p:|x﹣1|<2和命题q:﹣1<x<m+1,若p是q的充分不必要条件,则实数m的取值
范围
【答案】(2,+∞)
【解析】
试题分析:命题,命题,由p是q的充分不必要条件可得
考点:充分条件与必要条件
10.不等式ax2+4x+a>1﹣2x2对一切x∈R恒成立,则实数a的取值范围是
【答案】(2,+∞)
【解析】
试题分析:不等式ax2+4x+a>1﹣2x2对一切x∈R恒成立,
即(a+2)x2+4x+a-1>0对一切x∈R恒成立
若a+2=0,显然不成立
若a+2≠0,则解得a>2.
综上,a>2
考点:一元二次不等式的解法
11.已知xy=2x+y+2(x>1),则x+y的最小值为
【答案】7
【解析】
试题分析:∵xy=2x+y+2,∴,
∴
当且仅当即x=3时取等号
考点:基本不等式
12.已知F1,F2为椭圆+y2=1的左、右焦点,A为下顶点,连接AF2并延长交椭圆于点B,
则BF1长为 .
【答案】
【解析】
试题分析:椭圆的a= ,b=1,c=1,
即有F1(-1,0),F2(1,0),A(0,-1),
AF2的方程为y=x-1,
代入椭圆方程,
可得3x2-4x=0,
解得x=0或,
即有B(,),
则
考点:椭圆的简单性质
13.下列命题中为真命题的是 .
①命题“x∈R,x2+2>0”的否定; ②“若x2+y2=0,则x,y全为0”的否命题;
③ “全等三角形是相似三角形”的逆命题; ④“圆内接四边形对角互补”的逆否命题.
【答案】②④
【解析】
试题分析:①中原命题是真命题,所以否命题是假命题;②原命题的逆命题为:若x,y
全为0,在x2+y2=0为真命题,所以逆命题为真命题;③原命题的逆命题为相似三角形全等,是假命题;④中原命题是真命题,所以逆否命题是假命题
考点:四种命题
14.已知关于x的不等式x2-(4a+2)x+3a2+2a≤0(a>-1)的解集中恰好含有3个整数解,则a
的取值范围是 .
【答案】或
【解析】
试题分析:由x2-(4a+2)x+3a2+2a≤0,得(x-3a-2)(x-a)<0,
∵a>-1,∴不等式的解为a<x<3a+2,
-1<a≤0,-1<3a+2<2,整数解是0,1,不满足;
0<a<1,3≤3a+2<4,即,整数解是1,2,3,满足.
a>1,3a+2-a=2a+2>4,不满足.
综上,满足条件的a的取值范围是或
考点:一元二次不等式的解法
二、解答题:本大题共6小题,共计90分.请在答题卡指定区域内作答.解答时应写出文字说明、证明过程或演算步骤.
15.(本小题满分14分)
设命题p:关于x的函数y=(a﹣1)x为增函数;命题q:不等式﹣x2+2x﹣2≤a对一切实数均成立.若命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围.
【答案】.
【解析】
试题分析:利用一次函数与二次函数的单调性分别化简命题p,q,由命题“p或q”为真,且“p且q”为假,可得命题p、q一真一假.即可得出.
试题解析:当命题p为真命题时,a>2.
当命题q为真命题时,由﹣x2+2x﹣2=﹣(x﹣1)2﹣1≤﹣1,∴a≥﹣1.
由命题“p或q”为真,且“p且q”为假,可得命题p、q一真一假.
①当p真q假时,则,无解;
②当p假q真时,则,得﹣1≤a≤2,
∴实数a的取值范围是.
考点:复合命题的真假
16.(本小题满分14分)
在平面直角坐标系xOy中,已知椭圆C过点(0,2),其焦点为F1(﹣,0),F2(,0).
(1)求椭圆C的标准方程;
(2)已知点P在椭圆C上,且PF1=4,求△PF1F2的面积.
【答案】(1)(2)4
【解析】
试题分析:(1)设椭圆方程为=1,(a>b>0),由椭圆C过点(0,2),其焦点为
F2(﹣,0),F2(,0),求出a,b,c,由此能求出椭圆C的标准方程.(2)由点P在椭圆C上,且PF1=4,求出PF2,|F1F2|,由此能求出△PF1F2的面积.
试题解析:(1)∵椭圆C过点(0,2),其焦点为F2(﹣,0),F2(,0),
∴设椭圆方程为=1,(a>b>0),
则,∴ =3,
∴椭圆C的标准方程为=1.
(2)∵点P在椭圆C上,且PF1=4,∴PF2=2×3﹣4=2,∵F1(﹣,0),F2(,0),
∴|F1F2|=2,∴.∴PF1⊥PF2,
∴△PF1F2的面积S===4.
考点:直线与圆锥曲线的综合问题;椭圆的标准方程.
17.(本小题满分15分)
某房地产开发公司计划在一楼区内建造一个长方形公园ABCD,公园由长方形的休闲区A1B1C1D1(阴影部分)和环公园人行道组成.已知休闲区A1B1C1D1的面积为4000m2,人行道的宽分别为4m和10m.求:
(1)若设休闲区的长A1B1=xm,求公园ABCD所占面积S关于x的函数S(x)的解析式;
(2) 要使公园所占面积最小,休闲区A1B1C1D1的长和宽该如何设计?
【答案】(1) (2) 面积最小时长为100m,宽为40m
【解析】
考点:基本不等式在最值问题中的应用
18.(本小题满分15分)
设分别为椭圆的左、右两个焦点.
(1)若椭圆上的点到两点的距离之和等于4,写出椭圆的方程和焦点坐标;
(2)设点是(1)中所得椭圆上的动点,求线段的中点的轨迹方程.
【答案】(1),焦点坐标为(±1,0)(2)
【解析】
试题分析:(1)把点A的坐标代入椭圆方程,再由椭圆的定义知2a=4,从而求出椭圆的方程,由椭圆的方程求出焦点坐标.(2)设F1K的中点Q(x,y),则由中点坐标公式得点K(2x+1,2y),把K的坐标代入椭圆方程,化简即得线段KF1的中点Q的轨迹方程
试题解析:(1)由条件得
∴ ∴ ∴焦点坐标为(±1,0)
(2)设F1K中点为(x,y),K为(x0,y0)
则
又∵(x0,y0)在椭圆上 ∴ ∴
考点:圆锥曲线的轨迹问题;轨迹方程;椭圆的标准方程;椭圆的简单性质
19.(本小题满分16分)
已知关于的不等式.
(1)若此不等式的解集为,求实数的值;
(2)若,解关于的不等式
【答案】(1)(2)时,解集为,时,解集为;时,解集为;时,解集为;时,解集为
【解析】
试题分析:(1)利用三个二次关系可知与不等式对应的方程的根为,代入可得实数的值;(2)解不等式时需对a分情况讨论来解不等式,时为一次不等式,时为二次不等式,结合二次函数图像求解
试题解析:(1)由题意可知,……………………………………………………… 2分
和为方程的两根, 于是,…………… 4分
(2)①当时,由,得;………………………………… 6分
②当时,不等式可化为,解得或;… 8分
③当时,不等式可化为,
若,即,则,…………………………… 10分
若,即,则不等式解集为,…………………………… 12分
若,即,则.………………………………… 14分
综上,当时,不等式解集为;
当时,不等式解集为;
当时,则不等式解集为;
当时,不等式解集为;
当时,不等式解集为.……………………… 16分[
考点:三个二次关系与分情况讨论
20.(本小题满分16分)
已知函数
(1)若,解不等式;
(2)若不等式对一切实数恒成立,求实数的取值范围.
【答案】(1)(2)
【解析】
考点:绝对值不等式解法,不等式与函数的转化及函数求最值