【数学】2020届一轮复习（理）通用版14坐标系与参数方程作业 17页

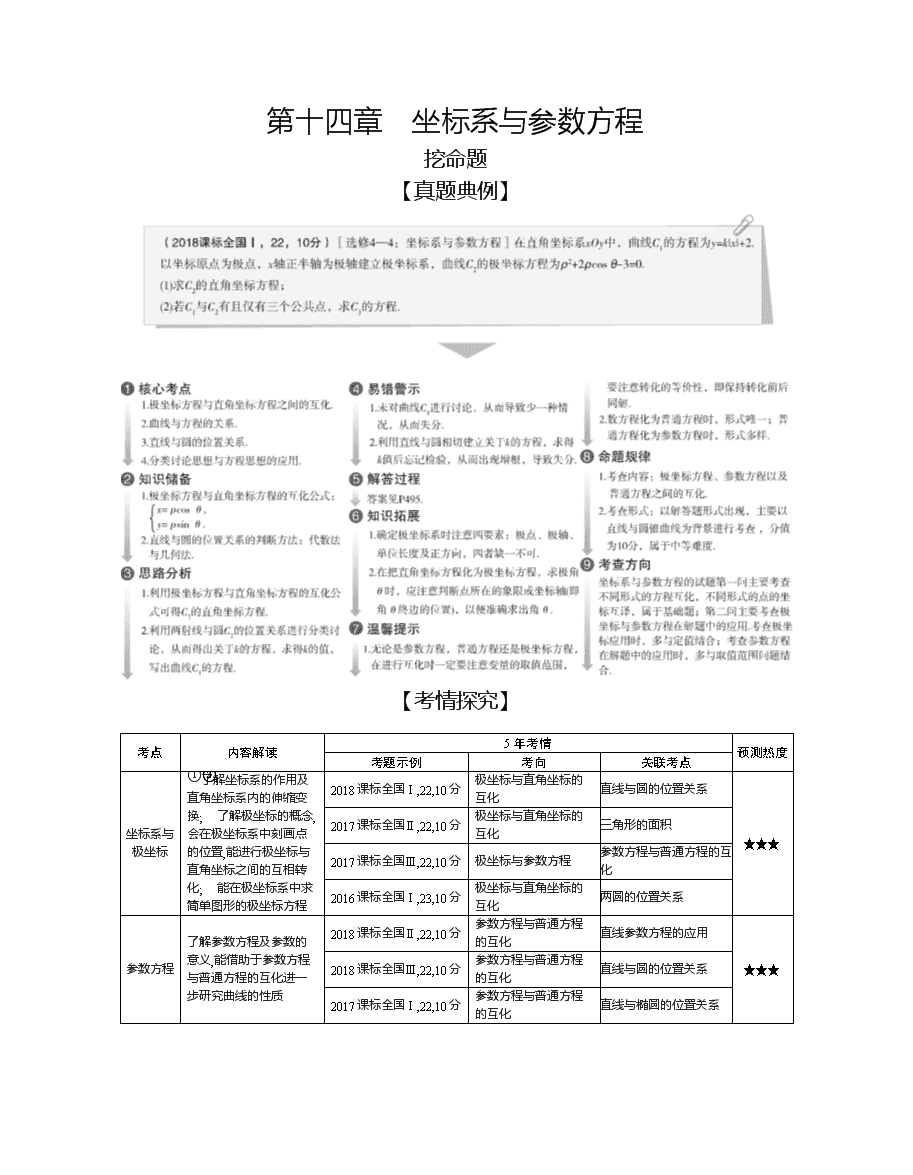
第十四章　坐标系与参数方程 挖命题 ‎【真题典例】‎ ‎【考情探究】‎ 考点 内容解读 ‎5年考情 预测热度 考题示例 考向 关联考点 坐标系与 极坐标 ‎①了解坐标系的作用及直角坐标系内的伸缩变换;②了解极坐标的概念,会在极坐标系中刻画点的位置,能进行极坐标与直角坐标之间的互相转化;③能在极坐标系中求简单图形的极坐标方程 ‎2018课标全国Ⅰ,22,10分 极坐标与直角坐标的互化 直线与圆的位置关系 ‎★★★‎ ‎2017课标全国Ⅱ,22,10分 极坐标与直角坐标的互化 三角形的面积 ‎2017课标全国Ⅲ,22,10分 极坐标与参数方程 参数方程与普通方程的互化 ‎2016课标全国Ⅰ,23,10分 极坐标与直角坐标的互化 两圆的位置关系 参数方程 了解参数方程及参数的意义,能借助于参数方程与普通方程的互化进一步研究曲线的性质 ‎2018课标全国Ⅱ,22,10分 参数方程与普通方程的互化 直线参数方程的应用 ‎★★★‎ ‎2018课标全国Ⅲ,22,10分 参数方程与普通方程的互化 直线与圆的位置关系 ‎2017课标全国Ⅰ,22,10分 参数方程与普通方程的互化 直线与椭圆的位置关系 分析解读　　坐标系与参数方程是高考的选考部分,重点考查直线与圆的极坐标方程,极坐标与直角坐标的互化;直线、圆与椭圆的参数方程以及参数方程与普通方程的互化.本章内容在高考中以极坐标方程或参数方程为载体,考查直线与圆以及直线与圆锥曲线的位置关系等知识,分值为10分,属于中档题.‎ 破考点 ‎【考点集训】‎ 考点一　坐标系与极坐标 ‎1.(2019届贵州贵阳9月调研,22)在直角坐标系xOy中,曲线C1的参数方程为x=2+2cosθ,‎y=2sinθ(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=‎3‎sin θ+cos θ,曲线C3的极坐标方程为θ=π‎6‎.‎ ‎(1)把曲线C1的参数方程化为极坐标方程;‎ ‎(2)曲线C3与曲线C1交于点O、A,与曲线C2交于点O、B,求|AB|.‎ 解析　(1)根据题意得曲线C1的普通方程为(x-2)2+y2=4,即x2+y2-4x=0.‎ 由x=ρcos θ,y=ρsin θ,得ρ2=4ρcos θ,‎ ‎∴曲线C1的极坐标方程为ρ=4cos θ.‎ ‎(2)设点A的极坐标为ρ‎1‎‎,‎π‎6‎(ρ1>0),点B的极坐标为ρ‎2‎‎,‎π‎6‎(ρ2>0),则ρ1=4cos π‎6‎=2‎3‎,ρ2=‎3‎sin π‎6‎+cos π‎6‎=‎3‎‎2‎+‎3‎‎2‎=‎3‎,∴|AB|=|ρ1-ρ2|=‎3‎.‎ ‎2.(2019届河南顶级名校第一次联考,22)在平面直角坐标系中,曲线C1:x2-y2=2,曲线C2的参数方程为x=2+2cosθ,‎y=2sinθ(θ为参数),以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系.‎ ‎(1)求曲线C1,C2的极坐标方程;‎ ‎(2)在极坐标系中,射线θ=π‎6‎与曲线C1,C2分别交于A,B两点(异于极点O),定点M(3,0),求△MAB的面积.‎ 解析　(1)根据题意得曲线C1的极坐标方程为ρ2cos2θ-ρ2sin2θ=2.‎ 由曲线C2的参数方程得曲线C2的普通方程为(x-2)2+y2=4,即x2+y2-4x=0,‎ ‎∴曲线C2的极坐标方程为ρ=4cos θ.‎ ‎(2)由(1)得点A的极坐标为‎2,‎π‎6‎,‎ 点B的极坐标为‎2‎3‎,‎π‎6‎.‎ ‎∴|AB|=|2-2‎3‎|=2‎3‎-2,‎ 定点M(3,0)到射线θ=π‎6‎(ρ≥0)的距离d=3sin π‎6‎=‎3‎‎2‎,‎ ‎∴△MAB的面积为‎1‎‎2‎|AB|·d=‎1‎‎2‎×(2‎3‎-2)×‎3‎‎2‎=‎3‎3‎-3‎‎2‎.‎ 考点二　参数方程 ‎1.(2019届广东珠海11月期中,22)已知倾斜角为α且经过点M(‎3‎,0)的直线l与椭圆C:x‎2‎‎4‎+y2=1交于A、B两点.‎ ‎(1)若α=π‎3‎,写出直线l与椭圆C的参数方程;‎ ‎(2)若‎|OM|‎‎|AB|‎=‎3‎‎3‎,求直线l的普通方程.‎ 解析　(1)直线l的参数方程为x=‎3‎+‎1‎‎2‎t,‎y=‎3‎‎2‎t(t为参数).‎ 椭圆C的参数方程为x=2cosθ,‎y=sinθ(θ为参数).‎ ‎(2)将直线l的参数方程x=‎3‎+tcosα,‎y=tsinα(t为参数)代入x‎2‎‎4‎+y2=1中,得(cos2α+4sin2α)t2+(2‎3‎cos α)t-1=0.‎ 设A,B对应的参数分别为t1,t2.‎ ‎∴t1+t2=-‎2‎3‎cosαcos‎2‎α+4sin‎2‎α,t1t2=-‎1‎cos‎2‎α+4sin‎2‎α,‎ ‎∴|AB|=|t1-t2|=‎(t‎1‎+t‎2‎‎)‎‎2‎-4‎t‎1‎t‎2‎=‎4‎cos‎2‎α+4sin‎2‎α=‎4‎‎1+3sin‎2‎α.‎ 由‎|OM|‎‎|AB|‎=‎3‎‎3‎得‎4‎‎1+3sin‎2‎α=3,∴sin2α=‎1‎‎9‎.‎ ‎∴直线l的普通方程为y=±‎2‎‎4‎(x-‎3‎).‎ ‎2.(2014课标Ⅰ,23,10分)已知曲线C:x‎2‎‎4‎+y‎2‎‎9‎=1,直线l:x=2+t,‎y=2-2t(t为参数).‎ ‎(1)写出曲线C的参数方程,直线l的普通方程;‎ ‎(2)过曲线C上任意一点P作与l夹角为30°的直线,交l于点A,求|PA|的最大值与最小值.‎ 解析　(1)曲线C的参数方程为x=2cosθ,‎y=3sinθ(θ为参数).‎ 直线l的普通方程为2x+y-6=0.‎ ‎(2)曲线C上任意一点P(2cos θ,3sin θ)到l的距离 d=‎5‎‎5‎|4cos θ+3sin θ-6|,‎ 则|PA|=dsin30°‎=‎2‎‎5‎‎5‎|5sin(θ+α)-6|,其中α为锐角,‎ 且tan α=‎4‎‎3‎.‎ 当sin(θ+α)=-1时,|PA|取得最大值,最大值为‎22‎‎5‎‎5‎.‎ 当sin(θ+α)=1时,|PA|取得最小值,最小值为‎2‎‎5‎‎5‎.‎ 炼技法 ‎【方法集训】‎ 方法1　极坐标方程与直角坐标方程的互化方法 ‎1.(2019届河南11月八市联考,22)在平面直角坐标系xOy中,动点P(x,y)的坐标满足x=t,‎y=‎t‎2‎(其中t∈R).在以O为极点,x轴的非负半轴为极轴的极坐标系(两种坐标系的单位长度相同)中,直线l的极坐标方程为ρsin(θ+φ)=cos φ其中φ为常数,且φ≠kπ+π‎2‎,k∈Z.‎ ‎(1)求动点P的轨迹C的极坐标方程(写成ρ=f(θ)的形式);‎ ‎(2)设直线l与轨迹C交于A、B两点,求证:当φ变化时,∠AOB的大小恒为定值.‎ 解析　(1)由x=t,‎y=‎t‎2‎消去参数t,得曲线C的直角坐标方程为x2=y.‎ 将x=ρcos θ,y=ρsin θ代入x2=y,得ρ2cos2θ=ρsin θ.‎ 所以曲线C的极坐标方程为ρ=sinθcos‎2‎θ.‎ ‎(2)证明:将l与C的极坐标方程联立,消去ρ得sinθsin(θ+φ)‎cos‎2‎θ=cos φ,展开得sinθ(sinθcosφ+cosθsinφ)‎cos‎2‎θ=cos φ.‎ 根据已知得cos φ≠0,于是可以得到tan2θ+tan φ·tan θ-1=0.‎ 设A(ρ1,θ1),B(ρ2,θ2),由根与系数的关系得tan θ1·tan θ2=-1.‎ 两边同乘cos θ1·cos θ2,可得cos(θ1-θ2)=0,解得θ1-θ2=kπ+π‎2‎(k∈Z).‎ 故当φ变化时,∠AOB的大小为定值π‎2‎.‎ ‎2.(2018四川德阳模拟,22)已知极坐标系的极点为平面直角坐标系xOy的原点,极轴为x轴正半轴,两种坐标系中的长度单位相同,曲线C的参数方程为x=-1+‎2‎cosα,‎y=1+‎2‎sinα(α为参数),直线l过点(-1,0),且斜率为‎1‎‎2‎,射线OM的极坐标方程为θ=‎3π‎4‎.‎ ‎(1)求曲线C和直线l的极坐标方程;‎ ‎(2)已知射线OM与曲线C的交点为O,P,与直线l的交点为Q,求线段PQ的长.‎ 解析　(1)∵曲线C的参数方程为x=-1+‎2‎cosα,‎y=1+‎2‎sinα(α为参数),‎ ‎∴曲线C的普通方程为(x+1)2+(y-1)2=2,‎ 将x=ρcos θ,y=ρsin θ代入整理得ρ+2cos θ-2sin θ=0,‎ 即曲线C的极坐标方程为ρ=2‎2‎sinθ-‎π‎4‎.‎ ‎∵直线l过点(-1,0),且斜率为‎1‎‎2‎,‎ ‎∴直线l的方程为y=‎1‎‎2‎(x+1),‎ ‎∴直线l的极坐标方程为ρcos θ-2ρsin θ+1=0.‎ ‎(2)当θ=‎3π‎4‎时,|OP|=2‎2‎sin‎3π‎4‎‎-‎π‎4‎=2‎2‎,‎ ‎|OQ|=‎1‎‎2×‎2‎‎2‎+‎‎2‎‎2‎=‎2‎‎3‎,‎ 故线段PQ的长为2‎2‎-‎2‎‎3‎=‎5‎‎2‎‎3‎.‎ 方法2　参数方程与普通方程的互化方法 ‎1.(2019届宁夏顶级名校第二次月考,22)在直角坐标系xOy中,直线l的参数方程为x=3-t,‎y=1+t(t为参数).在以坐标原点O为极点,x轴正半轴为极轴的极坐标系中,曲线C:ρ=2‎2‎cosθ-‎π‎4‎.‎ ‎(1)求直线l的普通方程和曲线C的直角坐标方程;‎ ‎(2)求曲线C上的点到直线l的距离的最大值.‎ 解析　(1)由x=3-t,‎y=1+t(t为参数)消去t得x+y-4=0,‎ 所以直线l的普通方程为x+y-4=0.‎ 由ρ=2‎2‎cosθ-‎π‎4‎=2‎2‎cosθcos π‎4‎+sinθsin ‎π‎4‎=2cos θ+2sin θ,得ρ2=2ρcos θ+2ρsin θ①.‎ 将ρ2=x2+y2,ρcos θ=x,ρsin θ=y代入①式,‎ 得x2+y2=2x+2y,即(x-1)2+(y-1)2=2.‎ 所以曲线C的直角坐标方程为(x-1)2+(y-1)2=2.‎ ‎(2)设曲线C上的点P(1+‎2‎cos α,1+‎2‎sin α),‎ 则点P到直线l的距离d=‎|1+‎2‎cosα+1+‎2‎sinα-4|‎‎2‎=‎|‎2‎(sinα+cosα)-2|‎‎2‎=‎2sinα+‎π‎4‎-2‎‎2‎,当sinα+‎π‎4‎=-1时,dmax=2‎2‎.故曲线C上的点到直线l的距离的最大值为2‎2‎.‎ ‎2.(2018广东茂名二模,22)在平面直角坐标系xOy中,以原点O为极点,x轴的非负半轴为极轴,建立极坐标系,曲线C的极坐标方程为ρ=‎2cosθ‎1-cos‎2‎θ,直线l的参数方程为x=2+tcosα,‎y=1+tsinα(t为参数,0≤α<π).‎ ‎(1)若α=‎3π‎4‎,求l的普通方程,直接写出C的直角坐标方程;‎ ‎(2)若l与C有两个不同的交点A,B,且P(2,1)为AB的中点,求|AB|.‎ 解析　(1)由直线l的参数方程x=2+tcosα,‎y=1+tsinα(t为参数)及α=‎3π‎4‎可得其直角坐标方程为x+y-3=0,‎ 由曲线C的极坐标方程ρ=‎2cosθ‎1-cos‎2‎θ,‎ 得其直角坐标方程为y2=2x.‎ ‎(2)把直线l的参数方程x=2+tcosα,‎y=1+tsinα(t为参数),‎ 代入抛物线方程y2=2x得 t2sin2α+2t(sin α-cos α)-3=0(*),‎ 设A,B所对应的参数分别为t1,t2,‎ 则t1+t2=-‎2(sinα-cosα)‎sin‎2‎α.‎ ‎∵P(2,1)为AB的中点,‎ ‎∴P点所对应的参数为t‎1‎‎+‎t‎2‎‎2‎=-sinα-cosαsin‎2‎α=0,‎ ‎∴sin α-cos α=0,‎ 即α=π‎4‎.‎ 则(*)变为‎1‎‎2‎t2-3=0,‎ 此时t2=6,t=±‎6‎,‎ ‎∴|AB|=2‎6‎.‎ 过专题 ‎【五年高考】‎ A组　统一命题·课标卷题组 考点一　坐标系与极坐标 ‎1.(2018课标全国Ⅰ,22,10分)[选修4—4:坐标系与参数方程]‎ 在直角坐标系xOy中,曲线C1的方程为y=k|x|+2.以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ2+2ρcos θ-3=0.‎ ‎(1)求C2的直角坐标方程;‎ ‎(2)若C1与C2有且仅有三个公共点,求C1的方程.‎ 解析　(1)由x=ρcos θ,y=ρsin θ得C2的直角坐标方程为(x+1)2+y2=4.‎ ‎(2)由(1)知C2是圆心为A(-1,0),半径为2的圆.‎ 由题设知,C1是过点B(0,2)且关于y轴对称的两条射线.‎ 记y轴右边的射线为l1,y轴左边的射线为l2.‎ 由于B在圆C2的外面,故C1与C2有且仅有三个公共点等价于l1与C2只有一个公共点且l2与C2有两个公共点,或l2与C2只有一个公共点且l1与C2有两个公共点.‎ 当l1与C2只有一个公共点时,A到l1所在直线的距离为2,所以‎|-k+2|‎k‎2‎‎+1‎=2,故k=-‎4‎‎3‎或k=0.‎ 经检验,当k=0时,l1与C2没有公共点;‎ 当k=-‎4‎‎3‎时,l1与C2只有一个公共点,l2与C2有两个公共点.‎ 当l2与C2只有一个公共点时,A到l2所在直线的距离为2,所以‎|k+2|‎k‎2‎‎+1‎=2,故k=0或k=‎4‎‎3‎.‎ 经检验,当k=0时,l1与C2没有公共点;‎ 当k=‎4‎‎3‎时,l2与C2没有公共点.‎ 综上,所求C1的方程为y=-‎4‎‎3‎|x|+2.‎ ‎2.(2017课标全国Ⅱ,22,10分)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,曲线C1的极坐标方程为ρcos θ=4.‎ ‎(1)M为曲线C1上的动点,点P在线段OM上,且满足|OM|·|OP|=16,求点P的轨迹C2的直角坐标方程;‎ ‎(2)设点A的极坐标为‎2,‎π‎3‎,点B在曲线C2上,求△OAB面积的最大值.‎ 解析　(1)设P的极坐标为(ρ,θ)(ρ>0),M的极坐标为(ρ1,θ)(ρ1>0).由题设知|OP|=ρ,|OM|=ρ1=‎4‎cosθ.‎ 由|OM|·|OP|=16得C2的极坐标方程为ρ=4cos θ(ρ>0).‎ 因此C2的直角坐标方程为(x-2)2+y2=4(x≠0).‎ ‎(2)设点B的极坐标为(ρB,α)(ρB>0).由题设知|OA|=2,ρB=4cos α,于是△OAB的面积S=‎1‎‎2‎|OA|·ρB·sin∠AOB ‎=4cos α·sinα-‎π‎3‎=2sin‎2α-‎π‎3‎-‎‎3‎‎2‎≤2+‎3‎.‎ 当α=-π‎12‎时,S取得最大值2+‎3‎.‎ 所以△OAB面积的最大值为2+‎3‎.‎ ‎3.(2016课标全国Ⅰ,23,10分)选修4—4:坐标系与参数方程 在直角坐标系xOy中,曲线C1的参数方程为x=acost,‎y=1+asint(t为参数,a>0).在以坐标原点为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=4cos θ.‎ ‎(1)说明C1是哪一种曲线,并将C1的方程化为极坐标方程;‎ ‎(2)直线C3的极坐标方程为θ=α0,其中α0满足tan α0=2,若曲线C1与C2的公共点都在C3上,求a.‎ 解析　(1)消去参数t得到C1的普通方程:x2+(y-1)2=a2.C1是以(0,1)为圆心,a为半径的圆.(2分)‎ 将x=ρcos θ,y=ρsin θ代入C1的普通方程中,得到C1的极坐标方程为ρ2-2ρsin θ+1-a2=0.(4分)‎ ‎(2)曲线C1,C2的公共点的极坐标满足方程组 ρ‎2‎‎-2ρsinθ+1-a‎2‎=0,‎ρ=4cosθ.‎‎(6分)‎ 若ρ≠0,由方程组得16cos2θ-8sin θcos θ+1-a2=0,(8分)‎ 由已知tan θ=2,可得16cos2θ-8sin θcos θ=0,从而1-a2=0,‎ 解得a=-1(舍去)或a=1.‎ a=1时,极点也为C1,C2的公共点,在C3上.‎ 所以a=1.(10分)‎ ‎4.(2016课标全国Ⅱ,23,10分)在直角坐标系xOy中,圆C的方程为(x+6)2+y2=25.‎ ‎(1)以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求C的极坐标方程;‎ ‎(2)直线l的参数方程是x=tcosα,‎y=tsinα(t为参数),l与C交于A,B两点,|AB|=‎10‎,求l的斜率.‎ 解析　(1)由x=ρcos θ,y=ρsin θ可得圆C的极坐标方程为ρ2+12ρcos θ+11=0.(3分)‎ ‎(2)在(1)中建立的极坐标系中,直线l的极坐标方程为θ=α(ρ∈R).‎ 设A,B所对应的极径分别为ρ1,ρ2,将l的极坐标方程代入C的极坐标方程得ρ2+12ρcos α+11=0.(6分)‎ 于是ρ1+ρ2=-12cos α,ρ1ρ2=11.‎ ‎|AB|=|ρ1-ρ2|=‎(ρ‎1‎+ρ‎2‎‎)‎‎2‎-4‎ρ‎1‎ρ‎2‎=‎144cos‎2‎α-44‎.(8分)‎ 由|AB|=‎10‎得cos2α=‎3‎‎8‎,tan α=±‎15‎‎3‎.‎ 所以l的斜率为‎15‎‎3‎或-‎15‎‎3‎.(10分)‎ ‎5.(2015课标Ⅰ,23,10分)在直角坐标系xOy中,直线C1:x=-2,圆C2:(x-1)2+(y-2)2=1,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.‎ ‎(1)求C1,C2的极坐标方程;‎ ‎(2)若直线C3的极坐标方程为θ=π‎4‎(ρ∈R),设C2与C3的交点为M,N,求△C2MN的面积.‎ 解析　(1)因为x=ρcos θ,y=ρsin θ,‎ 所以C1的极坐标方程为ρcos θ=-2,‎ C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+4=0.(5分)‎ ‎(2)将θ=π‎4‎代入ρ2-2ρcos θ-4ρsin θ+4=0,得ρ2-3‎2‎ρ+4=0,解得ρ1=2‎2‎,ρ2=‎2‎,故ρ1-ρ2=‎2‎,即|MN|=‎2‎.‎ 由于C2的半径为1,所以△C2MN的面积为‎1‎‎2‎.(10分)‎ 考点二　参数方程 ‎1.(2018课标全国Ⅲ,22,10分)[选修4—4:坐标系与参数方程]‎ 在平面直角坐标系xOy中,☉O的参数方程为x=cosθ,‎y=sinθ(θ为参数),过点(0,-‎2‎)且倾斜角为α的直线l与☉O交于A,B两点.‎ ‎(1)求α的取值范围;‎ ‎(2)求AB中点P的轨迹的参数方程.‎ 解析　(1)☉O的直角坐标方程为x2+y2=1.‎ 当α=π‎2‎时,l与☉O交于两点.‎ 当α≠π‎2‎时,记tan α=k,则l的方程为y=kx-‎2‎.‎ l与☉O交于两点当且仅当‎2‎‎1+‎k‎2‎<1,‎ 解得k<-1或k>1,‎ 即α∈π‎4‎‎,‎π‎2‎或α∈π‎2‎‎,‎‎3π‎4‎.‎ 综上,α的取值范围是π‎4‎‎,‎‎3π‎4‎.‎ ‎(2)l的参数方程为 x=tcosα,‎y=-‎2‎+tsinαt为参数,π‎4‎<α<‎‎3π‎4‎‎.‎ 设A,B,P对应的参数分别为tA,tB,tP,‎ 则tP=tA‎+‎tB‎2‎,且tA,tB满足t2-2‎2‎tsin α+1=0.‎ 于是tA+tB=2‎2‎sin α,tP=‎2‎sin α.‎ 又点P的坐标(x,y)满足x=tPcosα,‎y=-‎2‎+tPsinα,‎ 所以点P的轨迹的参数方程是 x=‎2‎‎2‎sin2α,‎y=-‎2‎‎2‎-‎2‎‎2‎cos2αα为参数,π‎4‎<α<‎‎3π‎4‎‎.‎ ‎2.(2017课标全国Ⅰ,22,10分)[选修4—4:坐标系与参数方程]‎ 在直角坐标系xOy中,曲线C的参数方程为x=3cosθ,‎y=sinθ(θ为参数),直线l的参数方程为x=a+4t,‎y=1-t(t为参数).‎ ‎(1)若a=-1,求C与l的交点坐标;‎ ‎(2)若C上的点到l距离的最大值为‎17‎,求a.‎ 解析　(1)解法一:曲线C的普通方程为x‎2‎‎9‎+y2=1.‎ 当a=-1时,直线l的普通方程为x+4y-3=0.‎ 由x+4y-3=0,‎x‎2‎‎9‎‎+y‎2‎=1‎解得x=3,‎y=0‎或x=-‎21‎‎25‎,‎y=‎24‎‎25‎.‎ 从而C与l的交点坐标为(3,0),‎-‎21‎‎25‎,‎‎24‎‎25‎.‎ 解法二:设交点坐标为(x,y),当a=-1时,‎ 直线l的参数方程为x=-1+4t,‎y=1-t.‎ 将x=3cosθ,‎y=sinθ代入x=-1+4t,‎y=1-t,‎ 得‎3cosθ+1‎‎4‎=1-sin θ,‎ 即3cos θ+4sin θ=3,3‎1-2sin‎2‎θ‎2‎+8sin θ‎2‎cos θ‎2‎=3,‎ 即2sin θ‎4cos θ‎2‎-3sin ‎θ‎2‎=0,‎ 由此可得sinθ‎2‎=0或tanθ‎2‎=‎4‎‎3‎,‎ 所以cosθ=1,‎sinθ=0‎或cosθ=‎3‎‎5‎,‎sinθ=‎4‎‎5‎,‎ 故可得交点坐标为(3,0)或‎-‎21‎‎25‎,‎‎24‎‎25‎.‎ ‎(2)直线l的普通方程为x+4y-a-4=0,故C上的点(3cos θ,sin θ)到l的距离为d=‎|3cosθ+4sinθ-a-4|‎‎17‎.‎ 当a≥-4时,d的最大值为a+9‎‎17‎,‎ 由题设得a+9‎‎17‎=‎17‎,‎ 所以a=8;‎ 当a<-4时,d的最大值为‎-a+1‎‎17‎,‎ 由题设得‎-a+1‎‎17‎=‎17‎,‎ 所以a=-16.‎ 综上,a=8或a=-16.‎ B组　自主命题·省(区、市)卷题组 考点一　坐标系与极坐标 ‎　(2018江苏,21C,10分)[选修4—4:坐标系与参数方程]‎ 在极坐标系中,直线l的方程为ρsinπ‎6‎‎-θ=2,曲线C的方程为ρ=4cos θ,求直线l被曲线C截得的弦长.‎ 解析　因为曲线C的极坐标方程为ρ=4cos θ,‎ 所以曲线C是圆心为(2,0),直径为4的圆,‎ 因为直线l的极坐标方程为ρsinπ‎6‎‎-θ=2,‎ 所以直线l过点(4,0),倾斜角为π‎6‎,‎ 设A(4,0),‎ 则A为直线l与圆C的一个交点.‎ 设另一个交点为B,则∠OAB=π‎6‎.‎ 连接OB,因为OA为直径,‎ 所以∠OBA=π‎2‎,‎ 所以AB=4cosπ‎6‎=2‎3‎.‎ 因此,直线l被曲线C截得的弦长为2‎3‎.‎ 考点二　参数方程 ‎1.(2017江苏,21C,10分)在平面直角坐标系xOy中,已知直线l的参数方程为x=-8+t,‎y=‎t‎2‎(t为参数),曲线C的参数方程为x=2s‎2‎,‎y=2‎2‎s(s为参数).设P为曲线C上的动点,求点P到直线l的距离的最小值.‎ 解析　直线l的普通方程为x-2y+8=0.‎ 因为点P在曲线C上,设P(2s2,2‎2‎s),‎ 从而点P到直线l的距离d=‎|2s‎2‎-4‎2‎s+8|‎‎1‎‎2‎‎+(-2‎‎)‎‎2‎=‎2(s-‎2‎‎)‎‎2‎+4‎‎5‎.‎ 当s=‎2‎时,dmin=‎4‎‎5‎‎5‎.‎ 因此当点P的坐标为(4,4)时,曲线C上点P到直线l的距离取到最小值‎4‎‎5‎‎5‎.‎ ‎2.(2016江苏,21C,10分)[选修4—4:坐标系与参数方程]‎ 在平面直角坐标系xOy中,已知直线l的参数方程为x=1+‎1‎‎2‎t,‎y=‎3‎‎2‎t(t为参数),椭圆C的参数方程为x=cosθ,‎y=2sinθ(θ为参数).设直线l与椭圆C相交于A,B两点,求线段AB的长.‎ 解析　椭圆C的普通方程为x2+y‎2‎‎4‎=1.‎ 将直线l的参数方程x=1+‎1‎‎2‎t,‎y=‎3‎‎2‎t代入x2+y‎2‎‎4‎=1,‎ 得‎1+‎1‎‎2‎t‎2‎+‎3‎‎2‎t‎2‎‎4‎=1,即7t2+16t=0,解得t1=0,t2=-‎16‎‎7‎.‎ 所以AB=|t1-t2|=‎16‎‎7‎.‎ C组　教师专用题组 考点一　坐标系与极坐标 ‎1.(2015湖南,12,5分)在直角坐标系xOy中,以坐标原点为极点,x轴的正半轴为极轴建立极坐标系.若曲线C的极坐标方程为ρ=‎ ‎2sin θ,则曲线C的直角坐标方程为　　　　　　. ‎ 答案　x2+y2-2y=0‎ ‎2.(2015广东,14,5分)(坐标系与参数方程选做题)在平面直角坐标系xOy中,以原点O为极点,x轴的正半轴为极轴建立极坐标系.曲线C1的极坐标方程为ρ(cos θ+sin θ)=-2,曲线C2的参数方程为x=t‎2‎,‎y=2‎2‎t(t为参数),则C1与C2交点的直角坐标为　　　　. ‎ 答案　(2,-4)‎ ‎3.(2014广东,14,5分)在极坐标系中,曲线C1与C2的方程分别为2ρcos2θ=sin θ与ρcos θ=1,以极点为平面直角坐标系的原点,极轴为x轴的正半轴,建立平面直角坐标系,则曲线C1与C2交点的直角坐标为　　　　. ‎ 答案　(1,2)‎ ‎4.(2015陕西,23,10分)在直角坐标系xOy中,直线l的参数方程为x=3+‎1‎‎2‎t,‎y=‎3‎‎2‎t(t为参数).以原点为极点,x轴正半轴为极轴建立极坐标系,☉C的极坐标方程为ρ=2‎3‎sin θ.‎ ‎(1)写出☉C的直角坐标方程;‎ ‎(2)P为直线l上一动点,当P到圆心C的距离最小时,求P的直角坐标.‎ 解析　(1)由ρ=2‎3‎sin θ,得 ρ2=2‎3‎ρsin θ,从而有x2+y2=2‎3‎y,所以x2+(y-‎3‎)2=3.‎ ‎(2)设P‎3+‎1‎‎2‎t,‎3‎‎2‎t,又C(0,‎3‎),‎ 则|PC|=‎3+‎1‎‎2‎t‎2‎‎+‎‎3‎‎2‎t-‎‎3‎‎2‎=t‎2‎‎+12‎,故当t=0时,|PC|取得最小值,此时,P点的直角坐标为(3,0).‎ ‎5.(2015课标Ⅱ,23,10分)选修4—4:坐标系与参数方程 在直角坐标系xOy中,曲线C1:x=tcosα,‎y=tsinα(t为参数,t≠0),其中0≤α<π.在以O为极点,x轴正半轴为极轴的极坐标系中,曲线C2:ρ=‎ ‎2sin θ,C3:ρ=2‎3‎cos θ.‎ ‎(1)求C2与C3交点的直角坐标;‎ ‎(2)若C1与C2相交于点A,C1与C3相交于点B,求|AB|的最大值.‎ 解析　(1)曲线C2的直角坐标方程为x2+y2-2y=0,曲线C3的直角坐标方程为x2+y2-2‎3‎x=0.‎ 联立x‎2‎‎+y‎2‎-2y=0,‎x‎2‎‎+y‎2‎-2‎3‎x=0,‎解得x=0,‎y=0‎或x=‎3‎‎2‎,‎y=‎3‎‎2‎.‎ 所以C2与C3交点的直角坐标为(0,0)和‎3‎‎2‎‎,‎‎3‎‎2‎.‎ ‎(2)曲线C1的极坐标方程为θ=α(ρ∈R,ρ≠0),‎ 其中0≤α<π.‎ 因此A的极坐标为(2sin α,α),B的极坐标为(2‎3‎cos α,α).‎ 所以|AB|=|2sin α-2‎3‎cos α|=4sinα-‎π‎3‎.‎ 当α=‎5π‎6‎时,|AB|取得最大值,最大值为4.‎ ‎6.(2013课标Ⅰ,23,10分)已知曲线C1的参数方程为x=4+5cost,‎y=5+5sint(t为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程为ρ=2sin θ.‎ ‎(1)把C1的参数方程化为极坐标方程;‎ ‎(2)求C1与C2交点的极坐标(ρ≥0,0≤θ<2π).‎ 解析　(1)将x=4+5cost,‎y=5+5sint消去参数t,化为普通方程(x-4)2+(y-5)2=25,即C1:x2+y2-8x-10y+16=0.‎ 将x=ρcosθ,‎y=ρsinθ代入x2+y2-8x-10y+16=0得 ρ2-8ρcos θ-10ρsin θ+16=0.‎ 所以C1的极坐标方程为ρ2-8ρcos θ-10ρsin θ+16=0.‎ ‎(2)C2的直角坐标方程为x2+y2-2y=0.‎ 由x‎2‎‎+y‎2‎-8x-10y+16=0,‎x‎2‎‎+y‎2‎-2y=0,‎ 解得x=1,‎y=1‎或x=0,‎y=2.‎ 所以C1与C2交点的极坐标分别为‎2‎‎,‎π‎4‎,‎2,‎π‎2‎.‎ 考点二　参数方程 ‎1.(2014湖南,12,5分)在平面直角坐标系中,曲线C:x=2+‎2‎‎2‎t,‎y=1+‎2‎‎2‎t(t为参数)的普通方程为　　　　　　　. ‎ 答案　x-y-1=0‎ ‎2.(2014课标Ⅱ,23,10分)在直角坐标系xOy中,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,半圆C的极坐标方程为ρ=‎ ‎2cos θ,θ∈‎0,‎π‎2‎.‎ ‎(1)求C的参数方程;‎ ‎(2)设点D在C上,C在D处的切线与直线l:y=‎3‎x+2垂直,根据(1)中你得到的参数方程,确定D的坐标.‎ 解析　(1)C的普通方程为(x-1)2+y2=1(0≤y≤1).‎ 可得C的参数方程为 x=1+cost,‎y=sint‎(t为参数,0≤t≤π).‎ ‎(2)设D(1+cos t,sin t).‎ 由(1)知C是以G(1,0)为圆心,1为半径的上半圆.‎ 因为C在点D处的切线与l垂直,所以直线GD与l的斜率相同.tan t=‎3‎,t=π‎3‎.‎ 故D的直角坐标为‎1+cosπ ‎‎3‎,sinπ‎3‎,即‎3‎‎2‎‎,‎‎3‎‎2‎.‎ ‎3.(2014辽宁,23,10分)将圆x2+y2=1上每一点的横坐标保持不变,纵坐标变为原来的2倍,得曲线C.‎ ‎(1)写出C的参数方程;‎ ‎(2)设直线l:2x+y-2=0与C的交点为P1,P2,以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求过线段P1P2的中点且与l垂直的直线的极坐标方程.‎ 解析　(1)设(x1,y1)为圆上的点,经变换为C上点(x,y),依题意,得x=x‎1‎,‎y=2y‎1‎.‎ 由x‎1‎‎2‎+y‎1‎‎2‎=1得x2+y‎2‎‎2‎=1,即曲线C的方程为x2+y‎2‎‎4‎=1.‎ 故C的参数方程为x=cost,‎y=2sint(t为参数).‎ ‎(2)由x‎2‎‎+y‎2‎‎4‎=1,‎‎2x+y-2=0‎解得x=1,‎y=0‎或x=0,‎y=2.‎ 不妨令P1(1,0),P2(0,2),则线段P1P2的中点坐标为‎1‎‎2‎‎,1‎,所求直线斜率为k=‎1‎‎2‎,于是所求直线方程为y-1=‎1‎‎2‎x-‎‎1‎‎2‎,化为极坐标方程,并整理得2ρcos θ-4ρsin θ=-3,即ρ=‎3‎‎4sinθ-2cosθ.‎ ‎4.(2013课标Ⅱ,23,10分)已知动点P,Q都在曲线C:x=2cost,‎y=2sint(t为参数)上,对应参数分别为t=α与t=2α(0<α<2π),M为PQ的中点.‎ ‎(1)求M的轨迹的参数方程;‎ ‎(2)将M到坐标原点的距离d表示为α的函数,并判断M的轨迹是否过坐标原点.‎ 解析　(1)依题意有P(2cos α,2sin α),Q(2cos 2α,2sin 2α),因此M(cos α+cos 2α,sin α+sin 2α).‎ M的轨迹的参数方程为x=cosα+cos2α,‎y=sinα+sin2α(α为参数,0<α<2π).‎ ‎(2)M点到坐标原点的距离d=x‎2‎‎+‎y‎2‎=‎2+2cosα(0<α<2π).当α=π时,d=0,故M的轨迹过坐标原点.‎ ‎5.(2012课标全国,23,10分)已知曲线C1的参数方程是x=2cosφ,‎y=3sinφ(φ为参数),以坐标原点为极点,x轴的正半轴为极轴建立极坐标系,曲线C2的极坐标方程是ρ=2.正方形ABCD的顶点都在C2上,且A,B,C,D依逆时针次序排列,点A的极坐标为‎2,‎π‎3‎.‎ ‎(1)求点A,B,C,D的直角坐标;‎ ‎(2)设P为C1上任意一点,求|PA|2+|PB|2+|PC|2+|PD|2的取值范围.‎ 解析　(1)由已知可得A‎2cosπ‎3‎,2sinπ‎3‎,B2cosπ‎3‎+π‎2‎,2sinπ‎3‎+π‎2‎,C2cosπ‎3‎+π,2sinπ‎3‎+π,D2cosπ‎3‎+‎3π‎2‎,2sinπ‎3‎+‎3π‎2‎,‎ 即A(1,‎3‎),B(-‎3‎,1),C(-1,-‎3‎),D(‎3‎,-1).‎ ‎(2)设P(2cos φ,3sin φ),令S=|PA|2+|PB|2+|PC|2+|PD|2,则S=16cos2φ+36sin2φ+16=32+20sin2φ.‎ 因为0≤sin2φ≤1,所以S的取值范围是[32,52].‎ ‎6.(2011课标,23,10分)在直角坐标系xOy中,曲线C1的参数方程为x=2cosα,‎y=2+2sinα(α为参数),M是C1上的动点,P点满足OP=2OM,P点的轨迹为曲线C2.‎ ‎(1)求C2的方程;‎ ‎(2)在以O为极点,x轴的正半轴为极轴的极坐标系中,射线θ=π‎3‎与C1的异于极点的交点为A,与C2的异于极点的交点为B,求|AB|.‎ 解析　(1)设P(x,y),则由条件知Mx‎2‎‎,‎y‎2‎.由于M点在C1上,所以x‎2‎‎=2cosα,‎y‎2‎‎=2+2sinα.‎即x=4cosα,‎y=4+4sinα.‎ 从而C2的参数方程为x=4cosα,‎y=4+4sinα(α为参数).‎ ‎(2)曲线C1的极坐标方程为ρ=4sin θ,曲线C2的极坐标方程为ρ=8sin θ.‎ 射线θ=π‎3‎与C1的交点A的极径为ρ1=4sinπ‎3‎,射线θ=π‎3‎与C2的交点B的极径为ρ2=8sinπ‎3‎.‎ 所以|AB|=|ρ2-ρ1|=2‎3‎.‎ ‎【三年模拟】‎ 时间:60分钟　分值:70分 解答题(共70分)‎ ‎1.(2019届四川成都摸底考试,22)在直角坐标系xOy中,直线l的参数方程为x=1+‎1‎‎2‎t,‎y=1+‎3‎‎2‎t(t为参数).在以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ2(1+2cos2θ)=3.‎ ‎(1)写出直线l的普通方程与曲线C的直角坐标方程;‎ ‎(2)设点M(1,1),若直线l与曲线C相交于不同的两点A,B,求|AM|+|BM|的值.‎ 解析　(1)由直线l的参数方程消去参数t,得x-1=‎3‎‎3‎(y-1).‎ 化简,得直线l的普通方程为‎3‎x-y+1-‎3‎=0.‎ 将曲线C的极坐标方程化为ρ2+2ρ2cos2θ=3,‎ ‎∴x2+y2+2x2=3,‎ ‎∴曲线C的直角坐标方程为x2+y‎2‎‎3‎=1.‎ ‎(2)将直线l的参数方程代入x2+y‎2‎‎3‎=1中,得‎1+‎1‎‎2‎t‎2‎+‎1‎‎3‎·‎1+‎3‎‎2‎t‎2‎=1,‎ 化简,得t2+2×‎1+‎‎3‎‎3‎t+‎2‎‎3‎=0.‎ 此时Δ=‎8‎‎3‎+‎8‎‎3‎‎3‎>0.‎ 设A,B所对应的参数分别为t1,t2,‎ 由根与系数的关系,得t1+t2=-‎2+‎‎2‎‎3‎‎3‎,t1t2=‎2‎‎3‎.‎ 由直线参数的几何意义,知|AM|+|BM|=|t1|+|t2|=-t1-t2=2+‎2‎‎3‎‎3‎.‎ ‎2.(2019届广东顶级名校第三次联考,22)已知曲线C1的极坐标方程为ρ2cos 2θ=8,曲线C2的极坐标方程为θ=π‎6‎(ρ∈R),曲线C1,C2相交于A,B两点.‎ ‎(1)求A,B两点的极坐标;‎ ‎(2)曲线C1与直线x=1+‎3‎‎2‎t,‎y=‎1‎‎2‎t(t为参数)分别相交于M,N两点,求线段MN的长度.‎ 解析　(1)由ρ‎2‎cos2θ=8,‎θ=π‎6‎,‎得ρ2cos π‎3‎=8,‎ 所以ρ2=16,即ρ=±4.‎ 所以A,B两点的极坐标为A‎4,‎π‎6‎,B‎-4,‎π‎6‎或B‎4,‎‎7π‎6‎.‎ ‎(2)由曲线C1的极坐标方程得其直角坐标方程为x2-y2=8,‎ 将x=1+‎3‎‎2‎t,‎y=‎1‎‎2‎t(t为参数)代入x2-y2=8,‎ 整理得t2+2‎3‎t-14=0,设M,N对应的参数分别为t1,t2,则t1+t2=-2‎3‎,t1t2=-14,‎ 所以|MN|=‎(t‎1‎-‎t‎2‎‎)‎‎2‎=‎(t‎1‎+t‎2‎‎)‎‎2‎-4‎t‎1‎t‎2‎=‎(-2‎3‎‎)‎‎2‎-4×(-14)‎=2‎17‎.‎ ‎3.(2019届湖南衡阳10月调研,22)在平面直角坐标系xOy中,直线l过点P(1,0)且倾斜角为π‎3‎,在以O为极点,x轴的非负半轴为极轴的极坐标系中,曲线C的极坐标方程为ρ=4sinθ+‎π‎6‎.‎ ‎(1)求直线l的参数方程与曲线C的直角坐标方程;‎ ‎(2)若直线l与曲线C的交点分别为M,N,求‎1‎‎|PM|‎+‎1‎‎|PN|‎的值.‎ 解析　(1)由题意知,直线l的参数方程为x=1+‎1‎‎2‎t,‎y=‎3‎‎2‎t(t为参数).‎ ‎∵ρ=4sinθ+‎π‎6‎=2‎3‎sin θ+2cos θ,∴ρ2=2‎3‎ρsin θ+2ρcos θ.‎ ‎∵x=ρcos θ,y=ρsin θ,x2+y2=ρ2,‎ ‎∴x2+y2=2‎3‎y+2x,‎ ‎∴曲线C的直角坐标方程为(x-1)2+(y-‎3‎)2=4.‎ ‎(2)将直线l的参数方程x=1+‎1‎‎2‎t,‎y=‎3‎‎2‎t(t为参数)代入曲线C的直角坐标方程(x-1)2+(y-‎3‎)2=4,得t2-3t-1=0,设M,N对应的参数分别为t1,t2,∴t1+t2=3,t1t2=-1<0.‎ ‎∴‎1‎‎|PM|‎+‎1‎‎|PN|‎=‎1‎‎|t‎1‎|‎+‎1‎‎|t‎2‎|‎=‎|t‎1‎|+|t‎2‎|‎‎|t‎1‎t‎2‎|‎=‎|t‎1‎-t‎2‎|‎‎|t‎1‎t‎2‎|‎=‎(t‎1‎+t‎2‎‎)‎‎2‎-4‎t‎1‎t‎2‎‎|t‎1‎t‎2‎|‎=‎9+4‎‎1‎=‎13‎.‎ ‎4.(2019届广东韶关期中联考,22)在直角坐标系xOy中,已知曲线M的参数方程为x=1+2cosβ,‎y=1+2sinβ(β为参数),以原点为极点,x轴的正半轴为极轴建立极坐标系,直线l1的极坐标方程为θ=α,直线l2的极坐标方程为θ=α+π‎2‎.‎ ‎(1)写出曲线M的极坐标方程,并指出它是哪种曲线;‎ ‎(2)设l1与曲线M交于A,C两点,l2与曲线M交于B,D两点,求四边形ABCD面积的取值范围.‎ 解析　(1)由x=1+2cosβ,‎y=1+2sinβ(β为参数)消去参数β得(x-1)2+(y-1)2=4,‎ ‎∴曲线M是以(1,1)为圆心,2为半径的圆.‎ 将曲线M的直角坐标方程化成极坐标方程得ρ2-2ρ(sin θ+cos θ)-2=0,‎ ‎(2)设|OA|=ρ1,|OC|=ρ2,由l1与圆M的极坐标方程联立可得ρ2-2ρ(sin α+cos α)-2=0,‎ ‎∴ρ1+ρ2=2(sin α+cos α),ρ1·ρ2=-2.‎ ‎∵O,A,C三点共线,∴|AC|=|ρ1-ρ2|=‎(ρ‎1‎+ρ‎2‎‎)‎‎2‎-4ρ‎1‎·‎ρ‎2‎=‎12+4sin2α①,‎ 同理用α+π‎2‎代替α可得|BD|=‎12-4sin2α,易知l1⊥l2,‎ ‎∴S四边形ABCD=‎1‎‎2‎|AC|·|BD|=‎1‎‎2‎‎144-16sin‎2‎2α,‎ ‎∵sin22α∈[0,1],∴S四边形ABCD∈[4‎2‎,6].‎ ‎5.(2018河南洛阳二模,22)在直角坐标系xOy中,以O为极点,x轴的正半轴为极轴建立极坐标系,已知曲线C1的极坐标方程为 ρsin θ=4,曲线C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+1=0,曲线C3的极坐标方程为θ=π‎4‎(ρ∈R).‎ ‎(1)求C1与C2的直角坐标方程;‎ ‎(2)若C2与C1交于P点,C2与C3交于A,B两点,求△PAB的面积.‎ 解析　(1)∵曲线C1的极坐标方程为ρsin θ=4,‎ ‎∴曲线C1的直角坐标方程为y=4,‎ ‎∵曲线C2的极坐标方程为ρ2-2ρcos θ-4ρsin θ+1=0,‎ ‎∴曲线C2的直角坐标方程为x2+y2-2x-4y+1=0,‎ 即(x-1)2+(y-2)2=4.‎ ‎(2)∵曲线C3的极坐标方程为θ=π‎4‎(ρ∈R),‎ ‎∴曲线C3的直角坐标方程为y=x,‎ 联立C1与C2的方程得y=4,‎‎(x-1‎)‎‎2‎+(y-2‎)‎‎2‎=4,‎ 得x2-2x+1=0,‎ 解得x1=x2=1,‎ ‎∴点P的坐标为(1,4),‎ 点P到曲线C3的距离d=‎|1-4|‎‎2‎=‎3‎‎2‎‎2‎.‎ 设A(ρ1,θ1),B(ρ2,θ2).‎ 将θ=π‎4‎代入C2,得ρ2-3‎2‎ρ+1=0,‎ 则ρ1+ρ2=3‎2‎,ρ1ρ2=1,‎ ‎|AB|=|ρ1-ρ2|=‎(ρ‎1‎+ρ‎2‎‎)‎‎2‎-4‎ρ‎1‎ρ‎2‎=‎14‎,‎ ‎∴S△PAB=‎1‎‎2‎|AB|d=‎1‎‎2‎×‎14‎×‎3‎‎2‎‎2‎=‎3‎‎7‎‎2‎.‎ ‎6.(2018湖南岳阳二模,22)已知曲线C的极坐标方程是ρ=2cos θ,若以极点为平面直角坐标系的原点,极轴为x轴的正半轴,且取相同的单位长度建立平面直角坐标系,则直线l的参数方程是x=‎3‎‎2‎t+m,‎y=‎1‎‎2‎t(t为参数).‎ ‎(1)求曲线C的直角坐标方程与直线l的普通方程;‎ ‎(2)设点P(m,0),若直线l与曲线C交于A,B两点,且|PA|·|PB|=1,求非负实数m的值.‎ 解析　(1)由x=ρcos θ,y=ρsin θ,x2+y2=ρ2,‎ 曲线C的极坐标方程是ρ=2cos θ,即ρ2=2ρcos θ,‎ 得x2+y2=2x,即曲线C的直角坐标方程为(x-1)2+y2=1,‎ 由直线l的参数方程x=‎3‎‎2‎t+m,‎y=‎1‎‎2‎t(t为参数),‎ 可得其普通方程为x-‎3‎y-m=0.‎ ‎(2)将x=‎3‎‎2‎t+m,‎y=‎1‎‎2‎t(t为参数)代入圆(x-1)2+y2=1中,‎ 可得t2+‎3‎(m-1)t+m2-2m=0,‎ 由Δ=3(m-1)2-4(m2-2m)>0,可得-1