- 871.00 KB
- 2021-04-22 发布
高安二中2018—2019上学期高二期中考试
数学(文科)试题
考试时间:120分钟 分值:150分
命题人:熊芳升 校对人:敖龙
一、 选择题:(本大题共12小题,每小题5分,共60分.在每个小题给出的四个选项中,有且只有一项符合题目要求.)
1. 命题“若,则”的逆命题,否命题,逆否命题这三个命题中,真命题的个数是( )
A. 0 B. 1 C. 2 D. 3
2.下列双曲线中,渐近线方程为的是( )
3.设实数均不为零,则“成立”是“关于的不等式与的解集相同”的( )条件
A. 充分不必要 B.必要不充分 C.充要 D.既不充分也不必要
4.阅读如下程序框图,如果输出,那么空白的判断框中应填入的条件是( )
A. B. C. D.
5.从装有5个红球和3个白球的口袋内任取3个球,那么互斥而不对立的事件是( )
A. 至少有一个红球与都是红球 B. 至少有一个红球与都是白球
C. 恰有一个红球与恰有二个红球 D. 至少有一个红球与至少有一个白球
6.已知点P是边长为4的正方形内任一点,则P到四个顶点的距离均大于2的概率是( )
A. B. C. D.
7.设命题p:. 命题:若,则方程表示焦点在 轴上的椭圆.那么下列命题为真命题的是( )
8.齐王与田忌赛马,田忌的上等马优于齐王的中等马,劣于齐王的上等马,田忌的中等马优于齐王的下等马,劣于齐王的中等马, 田忌的下等马劣于齐王的下等马.现从双方的马匹中随机选一匹进行一场比赛,则田忌的马获胜的概率为( )
A. B. C. D.
9. 我国某颗人造地球卫星的运行轨迹是以地心F为一个焦点的椭圆,若它的近地点A距离地面m公里,远地点B距离地面M公里,地球半径为R公里,则该卫星轨迹的离心率e是( )
10. 为了解某校高三学生的视力情况,随机地抽查了该校100名高三学生的视力情况,得到频率分布直方图如下图,由于不慎将部分数据丢失,但知道前4组的频数成等比数列,后6组的频数成等差数列,设最大频率为a,视力在4.6到5.0之间的学生数为b,则a,b的值分别为 ( )
A 0.27;78 B 0.27;83
C 2.7;78 D 2.7,;3
11. 已知双曲线的右焦点为,若过且倾斜角为的直线
与双曲线的右支有两个交点,则此双曲线离心率的取值范围( )
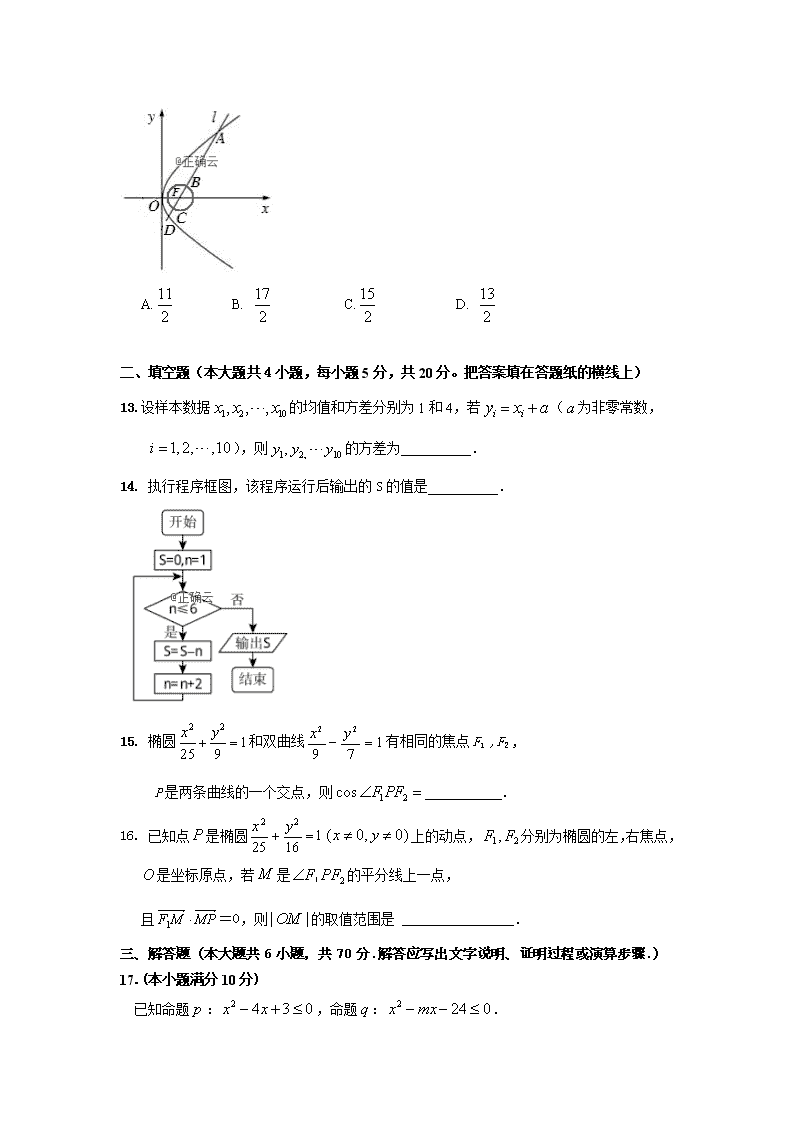
12.如图,已知抛物线的焦点为,直线过且依次交抛物线及圆于点四点,则的最小值为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,共20分。把答案填在答题纸的横线上)
13.设样本数据的均值和方差分别为1和4,若(为非零常数, ),则的方差为__________.
14. 执行程序框图,该程序运行后输出的S的值是__________.
15. 椭圆和双曲线有相同的焦点F1 ,F2 ,
P是两条曲线的一个交点,则 .
16. 已知点是椭圆上的动点,分别为椭圆的左,右焦点,是坐标原点,若是的平分线上一点,
且=0,则的取值范围是 .
三、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤.)
17.(本小题满分10分)
已知命题:,命题:.
(1) 若,为真命题,为假命题,求实数的取值范围;
(2) 若是的充分条件,求实数的取值范围.
18.(本小题满分12分)
某中学高二年级从甲、乙两个班级各选出7名学生参加数学竞赛,他们取得的成绩(满分100分)的茎叶图如图,其中甲班学生的平均分是85,乙班学生成绩的中位数是83.
(Ⅰ)求的值,并计算甲班7位学生成绩的方差;
(Ⅱ)从成绩在90分以上的学生中随机抽取两名学生,求甲班至少有一名学生的概率.
19.(本小题满分12分)
某市统计局就2015年毕业大学生的月收入情况调查了10000人,并根据所得数据画出样本的频率分布直方图所示,每个分组包括左端点,不包括右端点,如第一组表示.
(1)求毕业大学生月收入在的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析大学生的收入与所学专业、性别等方面的关系,还要再从这10000人中依工资收入按分层抽样方法抽出100人作进一步分析,则月收入在的这段应抽取多少人?
20.(本小题满分12分)
已知具有相关关系的两个变量之间的几组数据如下表所示:
(1)请根据上表数据在网格纸中绘制散点图;
(2)请根据上表提供的数据,用最小二乘法求出关于的线性回归方程,并估计当时,的值;
(3)将表格中的数据看作五个点的坐标,则从这五个点中随机抽取2个点,求这两个点都在直线的右下方的概率.
附参考公式:回归方程中中和最小二乘估计分别为
,
21. (本小题满分12分)
已知抛物线:的准线方程是
(1) 求抛物线的方程;
(2) 过点的直线与抛物线交于两点,设,
且恒成立,求实数的取值范围.
22.(本题满分12分)
已知椭圆过点,离心率为.
(Ⅰ)求椭圆的标准方程;
(Ⅱ)过椭圆的上顶点作直线交抛物线于、两点,为原点.
①求证:;
②设、分别与椭圆相交于、两点,过原点作直线的垂线,垂足为,证明:为定值.
高安二中2018—2019上学期高二期中考试
数学(文科)试题参考答案
一、 选择题:1. B 2.A 3. B 4.B 5.C 6.D 7.C 8.A 9.B 10.A 11. C 12.D
二、填空题 13. 4 14. -9 15. 16.(0,3)
三、解答题
17.(本小题满分10分)
(1)若真:,若真:,…………………………………2分
由已知,、一真一假.
①若真假,则,无解;………………………………………4分
②若假真,则,∴的取值范围为.…………6分
(2)对于:,由已知,对任意,恒成立,
故,故………………………………………10分
18.(本小题满分12分)
解:(I)∵甲班学生的平均分是85,
∴,
∴x=5,………………………………………………………………………………2分
∵乙班学生成绩的中位数是83,∴y=3;………………………………………4分
甲班7位学生成绩的方差为s2==40;…………………6分
(II)甲班成绩在90分以上的学生有两名,分别记为A,B,乙班成绩在90分以上的学生有三名,分别记为C,D,E,从这五名学生任意抽取两名学生共有10种情况:
(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E),(C,D),(C,E),
(D,E)………………………………………………………………………………8分
其中甲班至少有一名学生共有7种情况:(A,B),(A,C),(A,D),(A,E),(B,C),(B,D),(B,E).………………………………………………………………………………10分
记“从成绩在90分以上的学生中随机抽取两名学生,甲班至少有一名学生”为事件M,则.
答:从成绩在90分以上的学生中随机抽取两名学生,甲校至少有一名学生的概率为.…12分
19.(本小题满分12分)
解:(1)月收入在的频率为0.15 ……………………………………2分
(2)频率分布直方图知,中位数在,设中位数为,
则,解得,
根据频率分布直方图估计样本数据的中位数为;……………………………7分
(3)居民月收入在的频率为,
所以10000人中月收入在的人数为(人),
再从10000人用分层抽样方法抽出100人,
则月收入在的这段应抽取人.…………………………12分
20.(本小题满分12分)
(1)散点图如图所示:
………………………………………2分
(2)依题意,,,
,,
,∴;
∴回归直线方程为,故当时,.………………………7分
(3)五个点中落在直线右下方的三个点记为,另外两个点记为,从这五个点中任取两个点的结果有
共10个,
其中两个点均在直线的右下方的结果有3个,所以概率为.
………………………………………12分
A. (本小题满分12分)
解:(1)抛物线的准线方程是 , 解得 ,
抛物线的方程是. ---------------------------------------------------- 3´
(2)设直线方程是与联立,消去得, ,
设,则, -------------------------- 6´
, , - ---------------------- 8´
,
得对恒成立, - --------------------------------------- 10´
而解得 ---------------------------- 12´
22.(本题满分12分)
解:(1) ,所以
又,解得,,
所以椭圆的方程为 ………………………3分
(2)①证明:设、,依题意,直线一定有斜率, 的方程为,
联立方程消去得 ,
,又,,
………………………6分
②证明:设、,直线的方程为
,,
联立方程消去得 ,
,,
而
由 得
,即
. 所以为定值.
………………………………………12分