甘肃省白银市会宁县第一中学2019-2020学年高一上学期期中考试数学试题 15页

会宁一中2019-2020学年度第一学期期中考试 高一级数学试卷 一、选择题（本大题共12个小题，每小题5分，共60分，在每小题给出的四个选项中，只有一项是符合题目要求的）‎ ‎1.已知全集U＝{0,1,2,3,4,5,6}，集合A＝{0,1,2,3}，B＝{3,4,5}，则(∁UA)∩B等于 A. B. C. D. ‎ ‎【答案】B ‎【解析】‎ ‎【分析】‎ 首先进行补集运算，然后进行交集运算即可.‎ ‎【详解】由补集的定义可得：，‎ 则.‎ 本题选择B选项.‎ ‎【点睛】本题主要考查补集的运算，交集的运算，属于基础题.‎ ‎2.函数的定义域为（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ 依题意有，解得.‎ ‎3.下列四组函数，表示同一函数的是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 结合同一函数的概念，抓住定义域相等和对应关系相同来判断 ‎【详解】对，，对应关系不同，排除；‎ 对，定义域不同，中，中，排除；‎ 对C， 中，中或，定义域不同，排除；‎ 对D，，定义域和对应关系都相同；‎ 故选：‎ ‎【点睛】本题考查同一函数的判断方法，掌握两个基本原则：定义域相同，对应关系相同（化简之后的表达式相同），属于基础题 ‎4.已知函数且，则实数的值为（ ）‎ A. －1 B. ‎1 ‎C. －1或1 D. 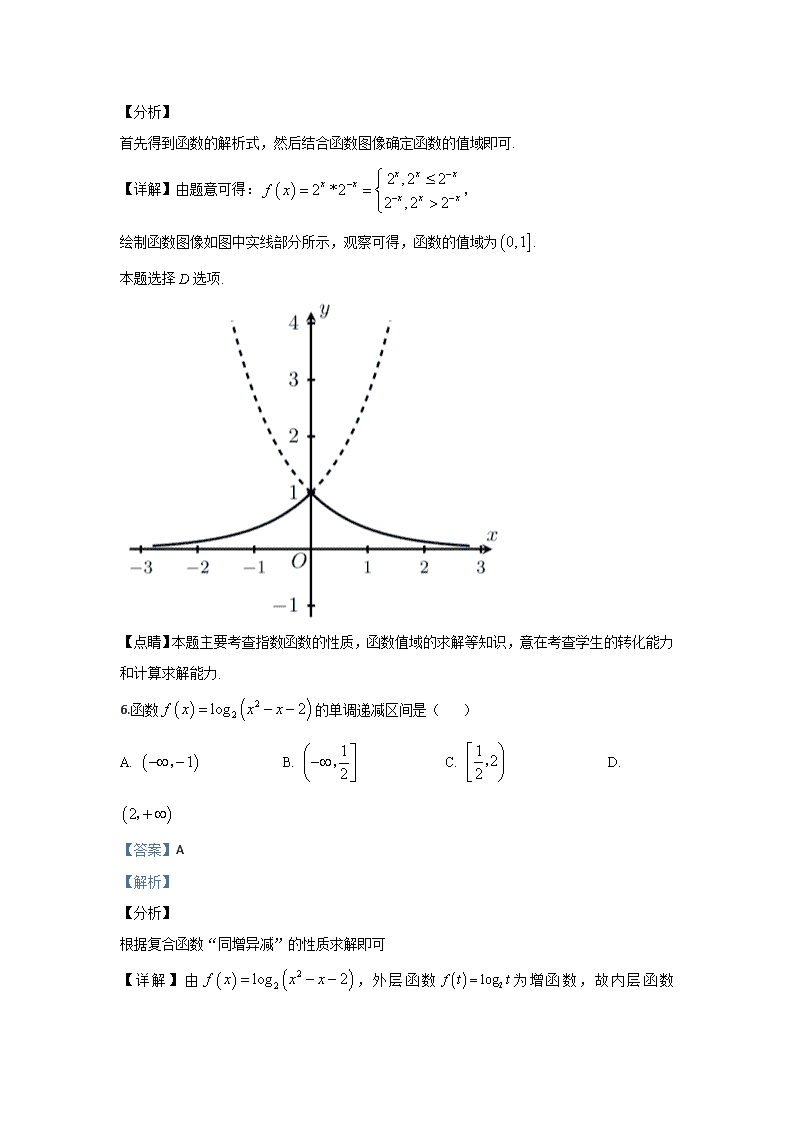－1或－‎ ‎【答案】C ‎【解析】‎ ‎【分析】‎ 结合分段函数解析式进行分类讨论即可求解自变量 ‎【详解】当时，；当时，，则 综上所述，的值为－1或1；‎ 故选：‎ ‎【点睛】本题考查分段函数中具体函数值的求法，属于基础题 ‎5.定义运算：，则函数的值域为 A. R B. (0，＋∞) C. [1，＋∞) D. (0，1]‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 首先得到函数的解析式，然后结合函数图像确定函数的值域即可.‎ ‎【详解】由题意可得：，‎ 绘制函数图像如图中实线部分所示，观察可得，函数的值域为.‎ 本题选择D选项.‎ ‎【点睛】本题主要考查指数函数的性质，函数值域的求解等知识，意在考查学生的转化能力和计算求解能力.‎ ‎6.函数的单调递减区间是（ ）‎ A. B. C. D. ‎ ‎【答案】A ‎【解析】‎ ‎【分析】‎ 根据复合函数“同增异减”的性质求解即可 ‎【详解】由，外层函数为增函数，故内层函数 应在符合定义域的基础上求单减区间，优先满足，即或，当时，单调递减；‎ 故选：‎ ‎【点睛】本题考查复合函数增减区间的求法，熟记“同增异减”是解题的关键，属于基础题 ‎7.设偶函数的定义域为R，当时，单调递减，则、、的大小关系是（ ）‎ A. B. ‎ C. D. ‎ ‎【答案】D ‎【解析】‎ ‎【分析】‎ 由偶函数的性质和函数的增减性辅以图像求解即可 ‎【详解】由题可画出拟合图像（不唯一），如图：‎ 可知，当越大，函数值越大，因，故 故选：‎ ‎【点睛】本题考查由函数的增减性与奇偶性解不等式，属于基础题 ‎8.在同一坐标系中，函数与（其中且）的图象的可能是（ ）‎ A. B. C. D. ‎ ‎【答案】C ‎【解析】‎ ‎【详解】对底数a讨论。如果a>1，则指数函数单调递减，对数函数递减，没有选项符合。当0‎0f(x)<0或{x<‎0f(x)>0.‎ 因为函数y=f(x)为偶函数,且在(−∞,0]上是减函数,又f(3)=0，‎ 所以f(x)在[0,+∞)是增函数，则对应的图象如图：‎ 所以解得x<−3或0