2018届二轮复习　磁场及带电粒子在磁场中的运动课件（共44张）（全国通用） 44页

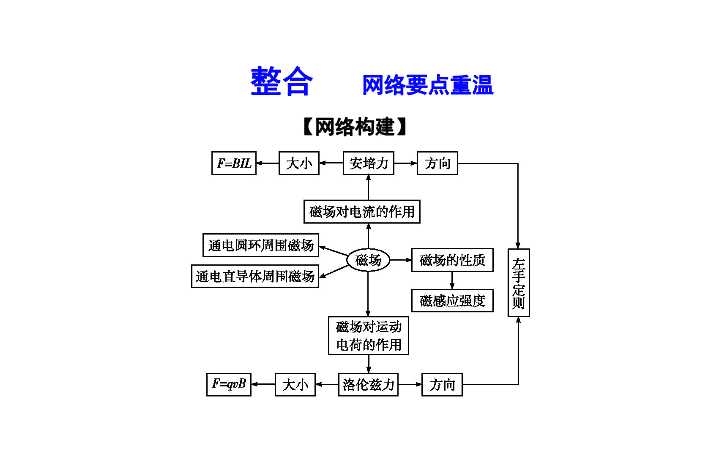
第 2 讲　磁场及带电粒子在磁场中的运动 整 合 突 破 实 战 整合 网络要点重温 【 网络构建 】 【 要点重温 】 1.安培力大小的计算公式: F=BILsin θ(其中θ为B与I之间的夹角). (1)若磁场方向和电流方向垂直:F=BIL. (2)若磁场方向和电流方向平行:F=0. 2.带电粒子在磁场中做匀速圆周运动 热点考向一　磁场的性质及磁场对电流的作用 【 核心提炼 】 “ 三步法 ” 分析通电导体棒受力 第1步:明确研究对象(通电导线或导体棒). 第2步:将题干中的立体图转化为平面图,明确磁场的方向和电流的方向. 第3步:受力分析的思路和力学完全相同,分析安培力时注意其方向一定与导体棒和磁感应强度组成的平面垂直. 突破 热点考向聚焦 【 典例 1】 (2017 · 全国 Ⅲ 卷 ,18) 如图 , 在磁感应强度大小为 B 0 的匀强磁场中 , 两长直导线 P 和 Q 垂直于纸面固定放置 , 两者之间的距离为 l. 在两导线中均通有方向垂直于纸面向里的电流 I 时 , 纸面内与两导线距离均为 l 的 a 点处的磁感应强度为零 . 如果让 P 中的电流反向、其他条件不变 , 则 a 点处磁感应强度的大小为 ( 　 　 ) C 【 预测练习 1】 (2017 · 山西孝义模拟 ) 如图所示 , 将长为 L 的密度和粗细均匀的金属棒 ab 的两端用两个劲度系数为 k 的相同的弹簧悬挂成水平状态 , 且位于垂直纸面向里的匀强磁场中 , 当金属棒中通过电流 I 1 , 时 , 弹簧恰好不伸长 ; 当电流方向由 b 到 a, 而电流大小为 I 2 (I 2 >I 1 ) 时 , 弹簧伸长量为 ( 　 　 ) A 热点考向二　带电粒子在匀强磁场中的匀速圆周运动　　 【 核心提炼 】 带电粒子在匀强磁场中做匀速圆周运动的解题方法 (1)四点:入射点B、出射点C、轨迹圆心A、入射速度直线与出射速度直线的交点O. (2)六线:圆弧两端点所在的轨迹半径r,入射速度直线OB和出射速度直线OC,入射点与出射点的连线BC,圆心与两条速度直线交点的连线AO. (3)三角:速度偏转角∠COD、圆心角∠BAC、弦切角∠OBC,其中偏转角等于圆心角,也等于弦切角的两倍. 【 典例 2】 (2017 · 全国 Ⅲ 卷 ,24) 如图 , 空间存在方向垂直于纸面 (xOy 平面 ) 向里的磁场 . 在 x≥0 区域 , 磁感应强度的大小为 B 0 ;x<0 区域 , 磁感应强度的大小为 λB 0 ( 常数 λ>1). 一质量为 m 、电荷量为 q(q>0) 的带电粒子以速度 v 0 从坐标原点 O 沿 x 轴正向射入磁场 , 此时开始计时 , 当粒子的速度方向再次沿 x 轴正向时 , 求 ( 不计重力 ) (1) 粒子运动的时间 ; (2) 粒子与 O 点间的距离 . 【 预测练习 2】 (2017 · 湖南岳阳模拟 ) 一半径为 R 的圆筒处于匀强磁场中 , 磁场方向与筒的轴平行 , 筒的横截面如图所示 . 图中直径 MN 的两端分别开有小孔 , 筒绕其中心轴以角速度 ω 顺时针转动 . 在该截面内 , 一质量为 m 、带电荷量为 q 的带电粒子从小孔 M 射入筒内 , 射入时的运动方向与 MN 成 30° 角 . 当筒转过 90° 时 , 该粒子恰好从小孔 N 飞出圆筒 . 不计粒子重力 , 若粒子在筒内未与筒壁发生碰撞 , 则关于带电粒子的运动半径 r 与磁场的磁感应强度 B 正确的是 ( 　 　 ) D 热点考向三　带电粒子在有界磁场中的临界极值问题 【 核心提炼 】 带电粒子在有界磁场中运动临界问题的三种几何关系 (1) 刚好穿出磁场边界的条件是带电粒子在磁场中运动的轨迹与边界相切 . (2) 当粒子的运动速率 v 一定时 , 粒子经过的弧长越长 , 圆心角越大 , 则带电粒子在有界磁场中运动的时间越长 . (3) 当粒子的运动速率 v 变化时 , 带电粒子在匀强磁场中的运动轨迹对应的圆心角越大 , 其在磁场中的运动时间越长 . 【典例3】 (2017 · 福建漳州二模) 如图,直角坐标系xOy中,A,C分别为x,y轴上的两点,OC长为L,∠OAC=30°,△OAC区域内有垂直于xOy平面向外的匀强磁场,区域外无磁场,有大量质量为m、电荷量为q的带正电粒子,以平行于y轴方向从OA边各处持续不断射入磁场,已知能从AC边垂直射出的粒子在磁场中的运动时间为t,不考虑粒子间的相互作用且粒子重力不计. (1)求磁场磁感应强度B的大小; (2)有些粒子的运动轨迹会与AC边相切,求相切轨迹的最大半径r m 及其对应的入射速度v m ; (3)若粒子入射速度相同,有些粒子能在边界AC上相遇,求相遇的粒子入射时间差的最大值. 〚 审题突破 〛 【 预测练习 3】 (2017 · 福建泉州模拟 )( 多选 ) 如图所示 , 在 x 轴上方存在着垂直于 xOy 平面向里、磁感应强度大小为 B 的匀强磁场 , 一个质量为 m 、电荷量为 e 的电子从 x 轴上的 A 点以速度 v 垂直磁场射入 , 射入方向与 x 轴正方向成 150°, 已知电子在磁场中运动的轨迹与 y 轴只有一个交点 , 下列说法正确的是 ( 　 　 ) ABD 热点考向四　带电粒子在复合场中的运动 【 核心提炼 】 1. 带电粒子在组合场中运动的处理方法 (1) 分别研究带电粒子在不同场区的运动规律 . 在匀强磁场中做匀速圆周运动 . 在匀强电场中 , 若速度方向与电场方向平行 , 则做匀变速直线运动 ; 若速度方向与电场方向垂直 , 则做类平抛运动 . (2) 带电粒子经过磁场区域时利用圆周运动规律结合几何关系处理 . (3) 当粒子从一个场进入另一个场时 , 该点的位置、粒子的速度大小和方向往往是解题的突破口 . 2. 带电粒子在叠加场中运动的处理方法 (1) 弄清叠加场的组成特点 . (2) 正确分析带电粒子的受力及运动特点 . (3) 画出粒子的运动轨迹 , 灵活选择不同的运动规律 . ① 若只有两个场 , 合力为零时 , 则表现为匀速直线运动或静止 . 例如电场与磁场中满足 qE=qvB; 重力场与磁场中满足 mg=qvB; 重力场与电场中满足 mg=qE. ② 若三场共存时 , 合力为零 , 粒子做匀速直线运动 , 其中洛伦兹力 F=qvB 的方向与速度 v 垂直 . ③ 若三场共存时 , 粒子做匀速圆周运动 , 则有 mg=qE, 粒子在洛伦兹力作用下做匀速圆周运动 . ④ 当带电粒子做复杂的曲线运动或有约束的变速直线运动时 , 一般用动能定理或能量守恒定律求解 . 3.几种常见的电磁场应用实例分析 中学阶段常见的带电粒子在正交的匀强电场和匀强磁场中运动的几种模型:①速度选择器;②回旋加速器;③质普仪;④磁流体发电机;⑤霍尔元件;⑥电磁流量计等.①,④,⑤和⑥的共同特征是粒子在其中只受电场力和洛伦兹力作用,并且最终电场力和洛伦兹力平衡. 【典例4】 (2017 · 江苏徐州模拟) 如图所示,位于竖直平面内的坐标系xOy,在其第三象限空间有垂直于纸面向外的匀强磁场,磁感应强度大小为B=0.5 T,还有沿x轴负方向的匀强电场,电场强度大小为E=2 N/C.在其第一象限空间有沿y轴负方向的、电场强度大小也为E的匀强电场,并在y>h=0.4 m的区域有磁感应强度也为B的垂直于纸面向里的匀强磁场.一个带电荷量为q的油滴从图中第三象限的P点得到一初速度,恰好能沿PO做匀速直线运动(PO与x轴负方向的夹角为θ=45°),并从原点O进入第一象限.已知重力加速度g=10 m/s 2 ,问: (1)油滴在第三象限运动时受到的重力、电场力、洛伦兹力三力的大小之比,并指出油滴带何种电荷; (2)油滴在P点得到的初速度大小; (3)油滴在第一象限运动的时间. 〚 审题指导 〛 【 预测练习 4】 (2017 · 河北衡水模拟 ) 如图 ( 甲 ) 所示 , 在真空中 , 半径为 b 的虚线所围的圆形区域内存在匀强磁场 , 磁场方向与纸面垂直 . 在磁场右侧有一对平行金属板 M 和 N, 两板间距离也为 b, 板长为 2b, 两板的中心线 O 1 O 2 与磁场区域的圆心 O 在同一直线上 , 两板左端与 O 1 也在同一直线上 . 有一电荷量为 +q 、质量为 m 的带电粒子 , 以速率 v 0 从圆周上的 P 点沿垂直于半径 OO 1 并指向圆心 O 的方向进入磁场 , 当从圆周上的 O 1 点飞出磁场时 , 给 M,N 板加上如图 ( 乙 ) 所示电压 u. 最后粒子刚好以平行于 N 板的速度 , 从 N 板的边缘飞出 . 不计平行金属板两端的边缘效应及粒子所受的重力 . (1) 求磁场的磁感应强度 B; (2) 求交变电压的周期 T 和电压 U 0 的值 ; (3) 若 t= 时 , 将该粒子从 MN 板右侧沿板的中心线 O 2 O 1 , 仍以速率 v 0 射入 M,N 之间 , 求粒子从磁场中射出的点到 P 点的距离 . 答案 : ( 3)2b 实战 高考真题演练 1.[ 粒子在叠加场中的运动 ] (2017 · 全国 Ⅰ 卷 ,16) 如图 , 空间某区域存在匀强电场和匀强磁场 , 电场方向竖直向上 ( 与纸面平行 ), 磁场方向垂直于纸面向里 , 三个带正电的微粒 a,b,c 电荷量相等 , 质量分别为 m a ,m b ,m c , 已知在该区域内 ,a 在纸面内做匀速圆周运动 ,b 在纸面内向右做匀速直线运动 ,c 在纸面内向左做匀速直线运动 . 下列选项正确的是 ( 　 　 ) A.m a >m b >m c B.m b >m a >m c C.m c >m a >m b D.m c >m b >m a B 解析 : 微粒 a 做匀速圆周运动的向心力由洛伦兹力提供 , 且 m a g=qE; 微粒 b 的受力关系为 m b g=qE+qv b B; 微粒 c 的受力关系为 m c g=qE-qv c B, 所以 m b >m a >m c , 选项 B 正确 . 2. [ 电磁技术的实际应用 ] (2016 · 全国 Ⅰ 卷 ,15) 现代质谱仪可用来分析比质子重很多倍的离子 , 其示意图如图所示 , 其中加速电压恒定 , 质子在入口处从静止开始被加速电场加速 , 经匀强磁场偏转后从出口离开磁场 . 若某种一价正离子在入口处从静止开始被同一加速电场加速 , 为使它经匀强磁场偏转后仍从同一出口离开磁场 , 需将磁感应强度增加到原来的 12 倍 . 此离子跟质子的质量比约为 ( 　 　 ) A.11 B.12 C.121 D.144 D 3. [ 粒子在匀强磁场中的圆周运动 ] (2017 · 全国 Ⅱ 卷 ,18) 如图 , 虚线所示的圆形区域内存在一垂直于纸面的匀强磁场 ,P 为磁场边界上的一点 . 大量相同的带电粒子以相同的速率经过 P 点 , 在纸面内沿不同方向射入磁场 . 若粒子射入速率为 v 1 , 这些粒子在磁场边界的出射点分布在六分之一圆周上 ; 若粒子射入速度为 v 2 , 相应的出射点分布在三分之一圆周上 , 不计重力及带电粒子之间的相互作用 . 则 v 2 ∶v 1 为 ( 　 　 ) C 4. [ 粒子在有界磁场中的临界问题 ] (2016 · 全国 Ⅲ 卷 ,18 ) 平面 OM 和平面 ON 之间的夹角为 30°, 其横截面 ( 纸面 ) 如图所示 , 平面 OM 上方存在匀强磁场 , 磁感应强度大小为 B, 方向垂直于纸面向外 . 一带电粒子的质量为 m, 电荷量为 q(q>0), 粒子沿纸面以大小为 v 的速度从 OM 的某点向左上方射入磁场 , 速度与 OM 成 30° 角 , 已知该粒子在磁场中的运动轨迹与 ON 只有一个交点 , 并从 OM 上另一点射出磁场 . 不计重力 . 粒子离开磁场的出射点到两平面交线 O 的距离为 ( 　 　 ) D 点击进入 提升 专题限时检测